进行科学的决策是项目评估工作中的主要目的之一。科学的决策方法就是对比判断,亦即对拟建项目的备选方案进行比选。但是,决策存在一定的风险性,项目评估工作中的大量决策基本是属于风险型决策。
概率分析为在风险条件下决定方案取舍的方法,决策树分析也是常用的风险决策方法之一。
所谓决策树分析,就是利用概率分析原理,用树状图描述备选方案的内容、参数、状态以及在实施过程中不同阶段方案的相互关系,对方案进行系统分析和评估的方法。应用决策树分析法不仅能进行单阶段决策,而且对多阶段决策也是行之有效的。
一、决策树的结构
决策树是以方框和圆圈为结点,并有直线连接而成的一种像树形状的图形,它是由以下几个因素构成:
(一)决策点与方案枝
某项决策的出发点,称为决策点,用方框"口"表示。方框内可用符号表示其为第几级决策点。
某项决策应有若干可供选择的方案,用从决策点引出的若干条直线“—”表示,叫做方案枝。在方案枝的上下侧可注明方案的含义及参数。
(二)状态结点与状态枝
方案在实施过程中由于存在风险性与不确定性,可能出现多种机会或状态,方案在各种自然状态下所能获得的结果(如收益或成本)用圆圈“○”表示,称为状态结点或机会点。
每一方案可能出现的各种状态用由状态结点引出的若干条线"—"表示,称为状态枝。各种状态的代号与概率等参数可标在状态上下侧,故又称其为概率枝。
(三)结果点与损益现值
方案在某种状态下可能获得的结果用“△”表示,称为结果点在结果点之后可分别列出其损益现值,所谓损益现值就是对方案在某种状态下损失或收益的度量结果的现值,即状态净现值。由
以上符号构成的图形像一棵树,所以称为决策树。如下图所示: 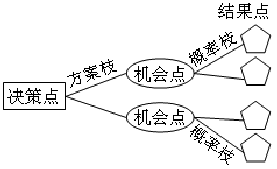
图 决策树
决策树作为一种决策工具,它分析简捷,形象直观,可以把决策问题的全部决策方案和可能出现的各种自然状态,以及不同自然状态下的结果,都形象地显示在全部的决策过程中。它是帮助项目评估人员进行分析比较方案的有用工具,近年来在项目评估工作中得到了广泛应用。
二、决策树分析的程序
(一)绘制决策树图
决策树图的绘制顺序是由左向右。根据需要决策的问题、可供选择的各种方案、各种方案的自然状态给出决策树图。
(二)计算收益现值、期望值
决策树分析的计算顺序是由右向左。
1.根据有关资料计算出各结果点的收益现值,并将其标在结果点后面。
2.根据各状态的收益现值和发生概率计算出各方案状态损益期望值,并将其标在状态结点上。
3.根据状态期望值与投资现值计算方案净现值的期望值,并将其标在方案枝上侧。
方案净现值的期望值=状态期望值-投资现值。
(三)决策选择
决策时遵循期望值原则,就是根据各方案的期望值进行决策。
1.若损益值用费用表示,应选择净现值的期望值最小的方案。
对落选的方案在其方案枝上画“×”,表示此枝已被"剪掉",称之为修枝。这样在决策树上只留下一条方案枝,即为最优方案。
2.若损益值用收益表示,应选择净现值的期望值最大的方案。
三、单阶段决策树
利用决策树进行决策时,凡只需要进行一次决策活动便可以选出最优方案,达到决策目的的决策,称为单级决策。把单级决策过程中各方案可能出现的自然状态概率和产生的结果绘成图形,就是单阶段决策树。
四、多阶段决策树
凡需要进行两次以上决策活动,才能选出最优方案,达到决策目的的决策,称为多级决策。把多级决策过程中各方案可能出现的自然状态、概率和产生的结果,都绘在一张图上,就形成多阶段决策树。
利用决策树进行多阶段决策要从最末一级决策点开始,并用各级决策后方案的期望值代替该级决策点缩减决策树,再逐级向前推移决策。
---------------------------------------------------
决策树方法
风险决策问题的直观表示方法的图示法。因为图的形状像树,所以被称为决策树,与决策矩阵表示法相比,决策树表示法有许多优点。如决策矩阵表示法只能表示单极决策问题,且要求所有行动方案所面对的自然状态完全一致。当利用决策树表示法时,决策矩阵表示法的缺点均能被克服,同时决策树表示法还方便简捷、层次清楚,能形象地显示决策过程。
决策树
的结构如图 所示。图中的方块代表决策节点,从它引出的分枝叫方案分枝。每条分枝代表一个方案,分枝数就是可能的相当方案数。圆圈代表方案的节点,从它引出的概率分枝,每条概率分枝上标明了自然状态及其发生的概率。概率分枝数反映了该方案面对的可能的状态数。末端的三角形叫结果点,注有各方案在相应状态下的结果值。
期望值的大小,确定方案的期望结果,然后根据不同方案的期望结果作出选择。方案的舍弃叫做修枝,被舍弃的方案用“≠”的记号来表示,最后的决策点留下一条树枝,即为最优方案。
当所要的决策问题只需进行一次决策就可解决,叫做单阶段决策问题。如果问题比较复杂,而要进行一系列的决策才能解决,就叫做多阶段决策问题,多阶段决策问题采用决策树决策方法比较直观容易。
例
为了适应市场的需要,某地提出了扩大电视机生产的两个方案。一个方案是建设大工厂,第二个方案是建设小工厂。建设大工厂需要投资600万元,可使用10年。建设小工厂投资280万元,如销路好,3年后扩建,扩建需要投资400万元,可使用7年,每年赢利190万元。试用决策树法选出合理的决策方案。
图9-4是例9.7的决策树,计算各点的期望值:
点②:0.7×200×10+.3×(-40)×10-600(投资)=680(万元)
点⑤:1.0×190×7-400=930(万元)
点⑥:1.0×80×7=560(万元)
比较决策点4的情况可以看到,由于点⑤(930万元)与点⑥(560万元)相比,点⑤的期望利润值较大,因此应采用扩建的方案,而舍弃不扩建的方案。把点⑤的930万元移到点4来,可计算出点③的期望利润值。
点③:0.7×80×3+0.7×930+0.3×60×(3+7)-280 = 719(万元)
图 例 的决策树
最后比较决策点1的情况。由于点③(719万元)与点②(680万元)相比,点③的期望利润值较大,因此取点③而舍点②。这样,相比之下,建设大工厂的方案不是最优方案,合理的策略应采用前3年建小工厂,如销路好,后7年进行扩建的方案。
决策树分析,不确定性分析
http://ggsygl.col.ynu.edu.cn/web_pb/plug3_dlfx/dlfx1/9/9_23.htm
http://wenku.baidu.com/view/9a2e543143323968011c92dc.html
http://wenku.baidu.com/view/517db98a84868762caaed502.html























