用遗传算法寻找迷宫出路

遗传算法是一种基于达尔文进化论的搜索启发式算法。该算法模拟了基于种群中最适合个体的自然选择。

遗传算法需要两个参数，即种群和适应度函数。根据适应度值在群体中选择最适合的个体。最健康的个体通过交叉和突变技术产生后代，创造一个新的、更好的种群。这个过程重复几代，直到得到最好的解决方案。

要解决的问题

本文中我们将使用遗传算法在迷宫中找到最短路径。

本文的的路径规划基于论文Autonomous Robot Navigation Using Genetic Algorithm with an Efficient Genotype Structure。

本文的代码基于两个假设：

1、代理不能对角线移动，也就是说只能左右，上下移动，不能走斜线。

2、迷宫的地图是已知的，但是代理不知道。

基因型

在由 N 列建模的导航环境中，路径可以由具有 N 个基因的基因型表示。 每个基因都是一个代表检查点坐标的元组。

所以我们的基因型如下，列式结构：

在列式结构中，我们假设每个基因都只放在一列中，例如，取一条大小为 8 的染色体，[(1,1), (4,2), (4,3), (6,4)， (2,5), (3,6), (7,7), (8,8)]。 它会像这样放置：

这里假设起始坐标是(1,1)，目标坐标是(8,8)

有两种方法可以从一个检查点移动到另一个检查点:

先排成一行移动 或 先排成一列移动

行移动：先在一行中移动，然后在列中移动。 如果我们从前面的例子中获取染色体，我们得到的路径是：

列移动：类似的，先在一列中移动，然后在一行中移动。 我们得到的路径是：

虽然这种基因型结构很好，但它不能为某些迷宫产生路径。 所以这种结构假定每个路径段都以连续的列结束。

实现遗传算法

本文使用python语言来实现遗传算法，并在最后有完整代码链接。

1、导入模块

这里的一个没见过的模块是pyamaze，它主要是python中生成迷宫。

fromrandomimportrandint, random, choice
 frompyamazeimportmaze, agent
 fromcopyimportdeepcopy, copy
 importcsv

2、定义常量和一些初始化

设置程序的不同参数并创建一个迷宫。

#initialize constants
 POPULATIONSIZE=120
 ROWS, COLS=16,8
 
 #Set the mutation rate 
 MUTATION_RATE=100
 
 # start and end points of the maze
 START, END=1, COLS
 
 #weights of path length, infeasible steps and number of turns
 wl, ws, wt=2, 3, 2
 
 #file name for storing fitness parameters
 file_name='data.csv'
 
 #initilize a maze object and create a maze 
 m=maze(ROWS, COLS)
 m.CreateMaze(loopPercent=100)
 maps=m.maze_map

3、种群的创建

此函数创建种群并为每个个体随机生成方向属性。

defpopFiller(pop, direction):
     """
     Takes in population and direction lists and fills them with random values within the range.
     """
     foriinrange(POPULATIONSIZE):
         # Generate a random path and add it to the population list
         pop.append([(randint(1, ROWS), j) forjinrange(1, COLS+1)])
         # Set the start and end points of the path
         pop[i][0] = (START, START)
         pop[i][-1] = (ROWS, END)
         # Generate a random direction and add it to the direction list
         direction.append(choice(["r", "c"]))
     returnpop, direction

4、路径计算

这一步使用了两个函数：inter_steps函数以两个坐标作为元组，例如(x, y)和方向信息来生成这些点之间的中间步数。path函数使用inter_steps函数通过循环每个个体的基因来生成它的路径。

definter_steps(point1, point2, direction):
     """
     Takes in two points and the direction of the path between them and returns the intermediate steps between them.
     """
     steps= []
     ifdirection=="c": # column first
         ifpoint1[0] <point2[0]:  
             steps.extend([(i, point1[1]) foriinrange(point1[0] +1, point2[0] +1)])
         elifpoint1[0] >point2[0]:
             steps.extend([(i, point1[1]) foriinrange(point1[0] -1, point2[0] -1, -1)])
         steps.append(point2)
     elifdirection=="r": # row first
         ifpoint1[0] <point2[0]:  
             steps.extend([(i, point1[1] +1) foriinrange(point1[0], point2[0] +1)])
         elifpoint1[0] >point2[0]:
             steps.extend([(i, point1[1] +1) foriinrange(point1[0], point2[0] -1, -1)])
         else:
             steps.append(point2)
     returnsteps
 
 defpath(individual, direction):
     """
     Takes in the population list and the direction list and returns the complete path using the inter_steps function.
     """
     complete_path= [individual[0]]
     foriinrange(len(individual) -1):
         # Get the intermediate steps between the current and the next point in the population
         complete_path.extend(inter_steps(individual[i], individual[i+1], direction))
     returncomplete_path

5、适应度评估

这个步骤使用两个函数来计算个体的适应度：pathParameters函数计算个体转弯次数和不可行步数，fitCal函数利用这些信息计算每个个体的适应度。 适应度计算的公式如下：

这些公式分别归一化了转身、不可行步长和路径长度的适应度。整体适应度计算公式如下所示:

wf, wl, wt是定义参数权重的常数，分别是不可行的步数，路径长度和转弯次数。这些常量之前已经初始化。

fitCal函数有一个额外的关键字参数，即createCSV，它用于将不同的参数写入CSV文件。

defpathParameters(individual, complete_path, map_data):
     """
     Takes in an individual, it's complete path and the map data
     and returns the number of turns and the number of infeasible steps.
     """
     # Count the number of turns in the individual's path
     turns=sum(
         1
         foriinrange(len(individual) -1)
         ifindividual[i][0] !=individual[i+1][0]
     )
     # Count the number of Infeasible steps in the individual's path
     infeas=sum(
         any(
             (
                 map_data[complete_path[i]]["E"] ==0andcomplete_path[i][1] ==complete_path[i+1][1] -1,
                 map_data[complete_path[i]]["W"] ==0andcomplete_path[i][1] ==complete_path[i+1][1] +1,
                 map_data[complete_path[i]]["S"] ==0andcomplete_path[i][0] ==complete_path[i+1][0] -1,
                 map_data[complete_path[i]]["N"] ==0andcomplete_path[i][0] ==complete_path[i+1][0] +1,
             )
         )
         foriinrange(len(complete_path) -1)
     )
     returnturns, infeas
 
 
 deffitCal(population, direction, solutions,createCSV=True):
     """
     Takes in the population list and the direction list and
     returns the fitness list of the population and the solution found(infeasible steps equal to zero).
     Args:
     - population (list): a list of individuals in the population
     - direction (list): a list of the direction for each individual
     - solutions (list): a list of the solutions found so far
     - createCSV (bool): a flag indicating whether to create a CSV file or not (default: True)
     """
     # Initialize empty lists for turns, infeasible steps, and path length
     turns= []
     infeas_steps= []
     length= []
     
     # A function for calculating the normalized fitness value
     defcalc(curr, maxi, mini):
         ifmaxi==mini:
             return0
         else:
             return1- ((curr-mini) / (maxi-mini))
 
     # Iterate over each individual in the population
     fori, individualinenumerate(population):
         # Generate the complete path of individual 
         p=path(individual, direction[i])
          # Calculate the number of turns and infeasible steps in the individual's path
         t, s=pathParameters(individual, p, maps)
         # If the individual has zero infeasible steps, add it to the solutions list
         ifs==0:
             solutions.append([deepcopy(individual), copy(direction[i])])
         # Add the individual's number of turns, infeasible steps, and path length to their respective lists
         turns.append(t)
         infeas_steps.append(s)
         length.append(len(p))
 
     # Calculate the maximum and minimum values for turns, infeasible steps, and path length
     max_t, min_t=max(turns), min(turns)
     max_s, min_s=max(infeas_steps), min(infeas_steps)
     max_l, min_l=max(length), min(length)
 
     # Calculate the normalized fitness values for turns, infeasible steps, and path length
     fs= [calc(infeas_steps[i], max_s, min_s) foriinrange(len(population))]
     fl= [calc(length[i],max_l, min_l) foriinrange(len(population))]
     ft= [calc(turns[i],  max_t, min_t) foriinrange(len(population))]
 
     # Calculate the fitness scores for each individual in the population
     fitness= [
         (100*ws*fs[i]) * ((wl*fl[i] +wt*ft[i]) / (wl+wt))
         foriinrange(POPULATIONSIZE)
     ]
 
     # If createCSV flag is True, write the parameters of fitness to a CSV file
     ifcreateCSV:
         withopen(file_name, 'a+', newline='') asf:
             writer=csv.DictWriter(f, fieldnames=['Path Length', 'Turns', 'Infeasible Steps', 'Fitness'])
             writer.writerow({'Path Length': min_l, 'Turns': min_t, 'Infeasible Steps': min_s, 'Fitness': max(fitness)})
     
     returnfitness, solutions

6、选择

这个函数根据适应度值对总体进行排序。

defrankSel(population, fitness, direction):
     """
     Takes in the population, fitness and direction lists and returns the population and direction lists after rank selection.
     """
     # Pair each fitness value with its corresponding individual and direction
     pairs=zip(fitness, population, direction)
     # Sort pairs in descending order based on fitness value
     sorted_pair=sorted(pairs, key=lambdax: x[0], reverse=True)
     # Unzip the sorted pairs into separate lists
     _, population, direction=zip(*sorted_pair)
 
     returnlist(population), list(direction)

7、交叉

这个函数实现了单点交叉。它随机选择一个交叉点，并使用种群人口的前一半(父母)来创建后一半，具体方法如下图所示：

defcrossover(population, direction):
     """ 
     Takes in the population and direction lists and returns the population and direction lists after single point crossover.
     """
     # Choose a random crossover point between the second and second-to-last gene
     crossover_point=randint(2, len(population[0]) -2)
     # Calculate the number of parents to mate (half the population size)
     no_of_parents=POPULATIONSIZE//2
     foriinrange(no_of_parents-1):
         # Create offspring by combining the genes of two parents up to the crossover point
         population[i+no_of_parents] = (
             population[i][:crossover_point] +population[i+1][crossover_point:]
         )
         # Choose a random direction for the offspring
         direction[i+no_of_parents] =choice(["r", "c"])
     returnpopulation, direction

8、变异

通过将基因(即tuple (x, y))的x值更改为范围内的任意数字来实现插入突变。元组的y值保持不变，因为我们假设迷宫中的每一列都应该只有一个检查点。

有几个参数可以调整，mutation_rate和no_of_genes_to_mutate。

defmutation(population, mutation_rate, direction, no_of_genes_to_mutate=1):
     """
     Takes in the population, mutation rate, direction and number of genes to mutate
     and returns the population and direction lists after mutation.
     """
     # Validate the number of genes to mutate
     ifno_of_genes_to_mutate<=0:
         raiseValueError("Number of genes to mutate must be greater than 0")
     ifno_of_genes_to_mutate>COLS:
         raiseValueError(
             "Number of genes to mutate must not be greater than number of columns"
         )
 
     foriinrange(POPULATIONSIZE):
         # Check if the individual will be mutated based on the mutation rate
         ifrandom() <mutation_rate:
             for_inrange(no_of_genes_to_mutate):
                 # Choose a random gene to mutate and replace it with a new random gene
                 index=randint(1, COLS-2)
                 population[i][index] = (randint(1, ROWS), population[i][index][1])
             # Choose a random direction for the mutated individual
             direction[i] =choice(["r", "c"])
     returnpopulation, direction

9、最佳解

该函数根据解的路径长度返回最佳解。

defbest_solution(solutions):
     """Takes a list of solutions and returns the best individual(list) and direction"""
     # Initialize the best individual and direction as the first solution in the list
     best_individual, best_direction=solutions[0]
     # Calculate the length of the path for the best solution
     min_length=len(path(best_individual, best_direction))
 
     forindividual, directioninsolutions[1:]:
         # Calculate the length of the path for the best solution
         current_length=len(path(individual, direction))
         # If the current solution is better than the best solution, update the best solution
         ifcurrent_length<min_length:
             min_length=current_length
             best_individual=individual
             best_direction=direction
     returnbest_individual, best_direction

10、整合

整个算法的工作流程就像我们开头显示的流程图一样，下面是代码：

defmain():
 
     # Initialize population, direction, and solution lists
     pop, direc, sol= [], [], []
     # Set the generation count and the maximum number of generations
     gen, maxGen=0, 2000
     # Set the number of solutions to be found
     sol_count=1
     # Set the number of solutions to be found
     pop, direc=popFiller(pop, direc)
 
     # Create a new CSV file and write header
     withopen(file_name, 'w', newline='') asf:
         writer=csv.DictWriter(f, fieldnames=['Path Length', 'Turns', 'Infeasible Steps', 'Fitness'])
         writer.writeheader()
 
     # Start the loop for the genetic algorithm
     print('Running...')
     whileTrue:
         gen+=1
         # Calculate the fitness values for the population and identify any solutions
         fitness, sol=fitCal(pop, direc, sol, createCSV=True)
         # Select the parents for the next generation using rank selection
         pop, direc=rankSel(pop, fitness, direc)
          # Create the offspring for the next generation using crossover
         pop, direc=crossover(pop, direc)
         # mutate the offsprings using mutation function
         pop, direc=mutation(pop, MUTATION_RATE, direc, no_of_genes_to_mutate=1)
         # Check if the required number of solutions have been found
         iflen(sol) ==sol_count:
             print("Solution found!")
             break
 
         # Check if the maximum number of generations have been reached
         ifgen>=maxGen:
             print("Solution not found!")
             flag=input("Do you  want to create another population(y/n): ")
             # if flag is 'y', clear the population and direction lists and refill them
             ifflag=='y':
                 pop, direc= [], []
                 pop, direc=popFiller(pop, direc)
                 gen=0
                 continue
              # If flag is 'n' exit the program
             else:
                 print("Good Bye")
                 returnNone
     
      # Find the best solution and its direction
     solIndiv, solDir=best_solution(sol)
     # Generate the final solution path and reverse it
     solPath=path(solIndiv, solDir)
     solPath.reverse()
 
      # Create an agent, set its properties, and trace its path through the maze
     a=agent(m, shape="square", filled=False, footprints=True)
     m.tracePath({a: solPath}, delay=100)
 
     m.run()
 
 if__name__=="__main__":
     # Call the main function
     main()

可视化和结果展示

最后为了能看到算法的过程，可以可视化不同参数随代数的变化趋势，使用matplotlib和pandas绘制曲线。

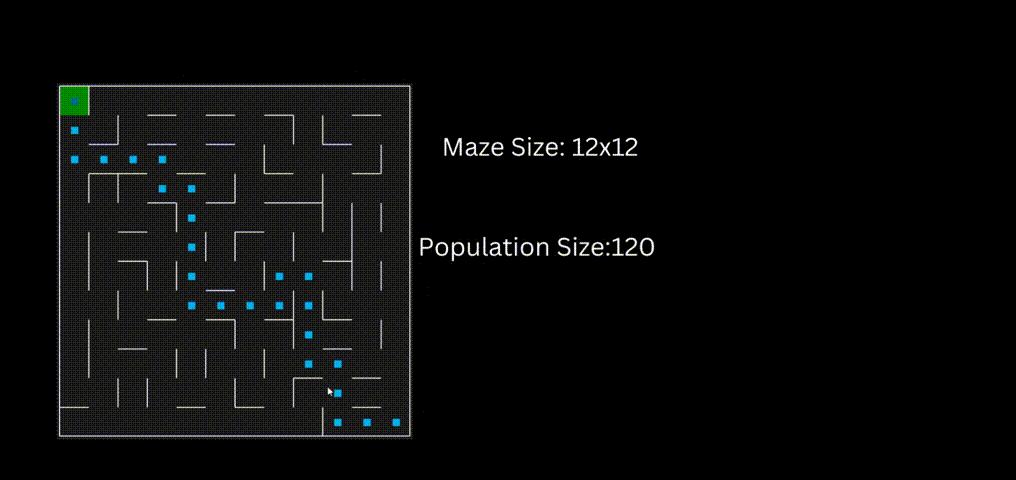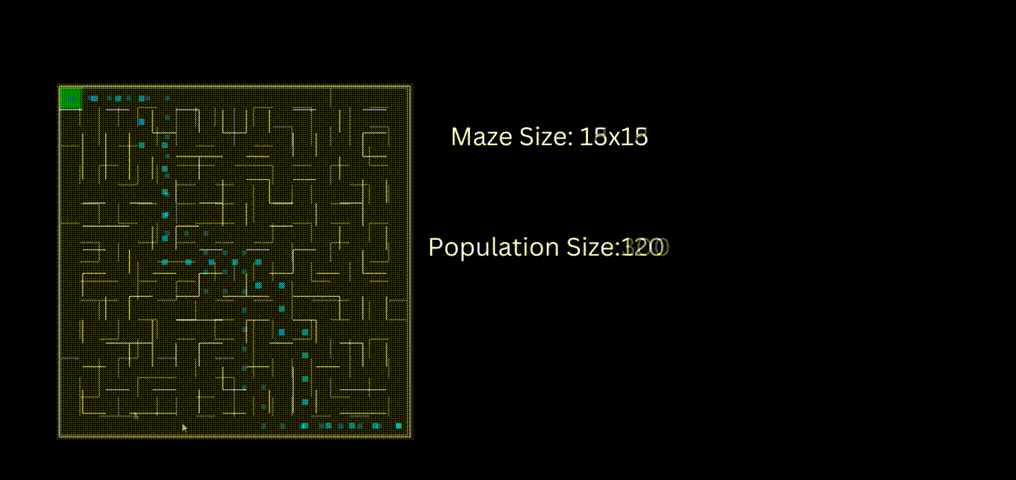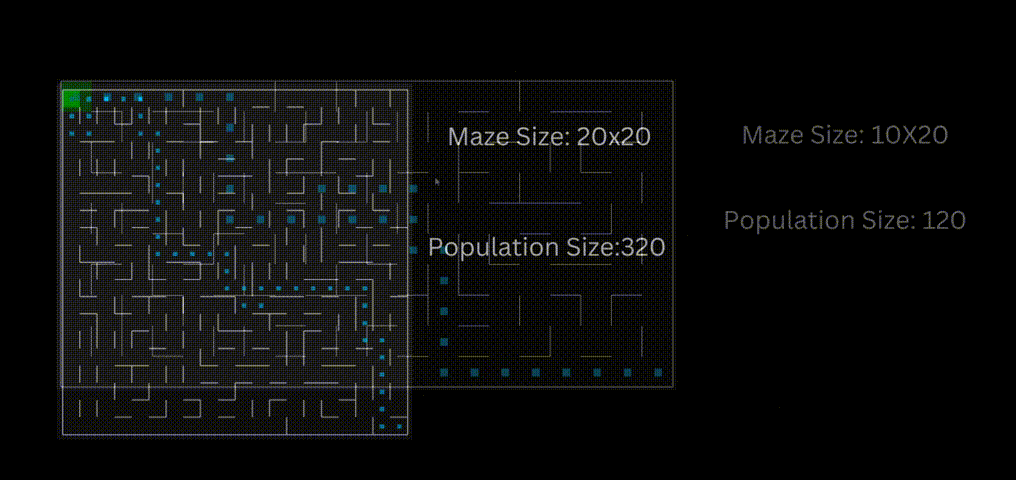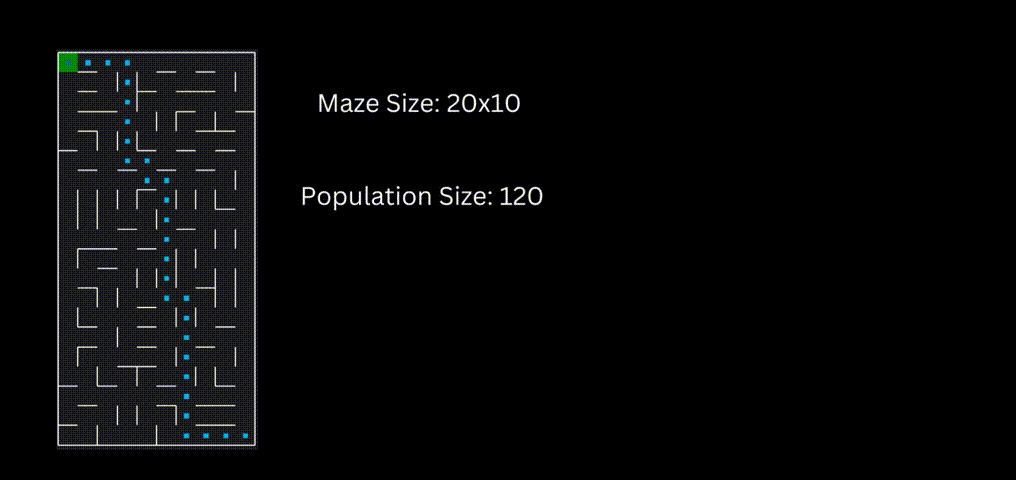
下面是一个使用“loopPercent = 100”的15 * 15迷宫的结果:

我们可以对他进行一些简单的分析：下图是我结果中得到的趋势线。“不可行的步数”显著减少，“路径长度”和“转弯数”也显著减少。经过几代之后，路径长度和转弯数变得稳定，表明算法已经收敛到一个解决方案。

适应度曲线不一致的可能原因:

当一个个体在种群中的适应度最大时，不意味着它就是解决方案。但它继续产生越来越多的可能解，如果一个群体包含相似的个体，整体的适合度会降低。

下面一个是是使用“loopPercent = 100”的10 * 20迷宫的结果:

趋势线与之前的迷宫相似：

使用“loopPercent = 100”的12 × 12迷宫的结果:

程序运行后找到的三个解决方案，并从中选择最佳解决方案。红色的是最佳方案。最佳解决方案是根据路径长度等标准选择的。与其他解决方案相比，红色代理能够找到通过迷宫的有效路径。这些结果证明了该方案的有效性。

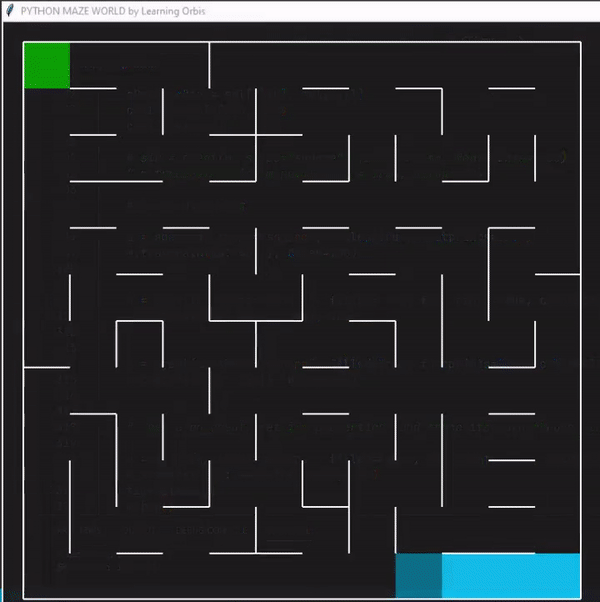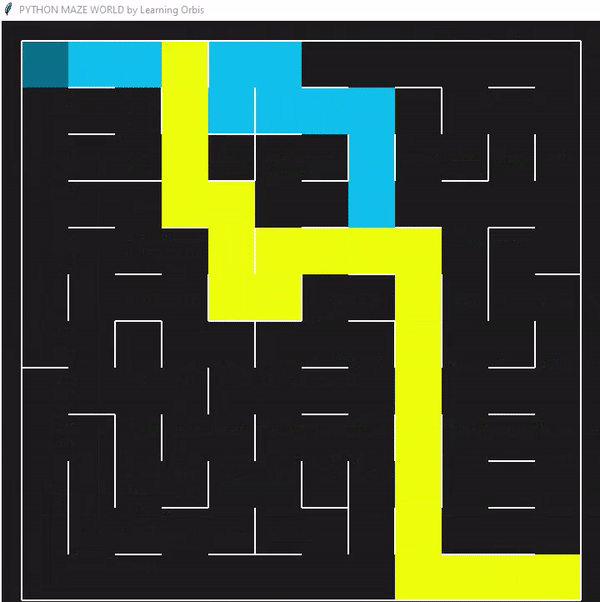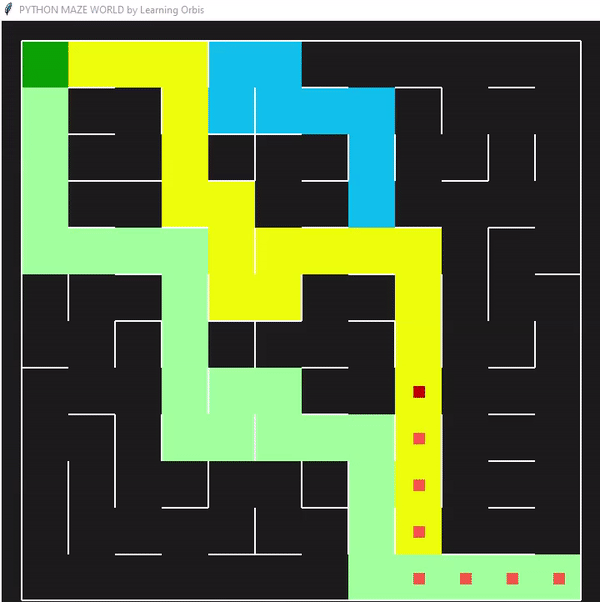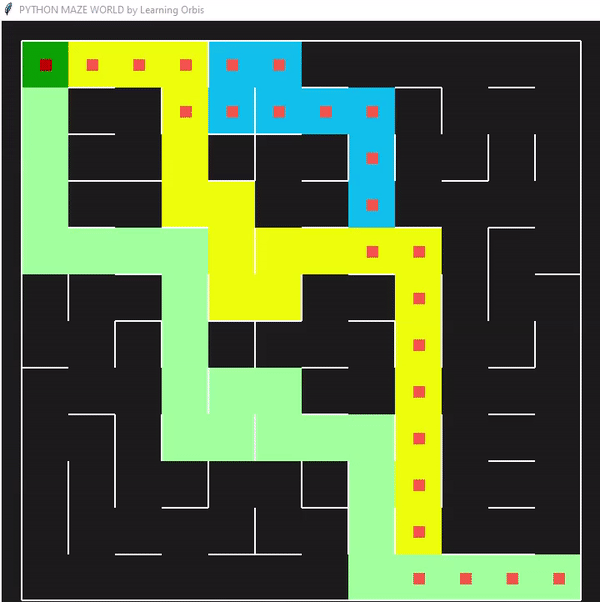
一些数据指标的对比

计算了10个不同大小的迷宫的解决方案所需时间的数据。

随着迷宫规模的增加，时间几乎呈指数增长。这意味着用这种算法解决更大的迷宫是很有挑战性的。

这是肯定的：

因为遗传算法是模拟的自然选择，有一定的随机性，所以计算量很大，特别是对于大而复杂的问题。我们选择的实现方法也适合于小型和简单的迷宫，基因型结构不适合大型和复杂的迷宫。迷宫的结果也取决于初始总体，如果初始总体是好的，它会更快地收敛到解决方案，否则就有可能陷入局部最优。遗传算法也不能找到最优解。

总结

本文我们成功地构建并测试了一个解决迷宫的遗传算法实现。对结果的分析表明，该算法能够在合理的时间内找到最优解，但随着迷宫大小的增加或loopPercent的减少，这种实现就会变得困难。参数POPULATION_SIZE和mutation_rate，对算法的性能有重大影响。本文只是对遗传算法原理的一个讲解，可以帮助你了解遗传算法的原理，对于小型数据可以实验，但是在大型数据的生产环境，请先进行优化。

作者：Dayan Hafeez