Nearest Common Ancestors
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 19636Accepted: 10412
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
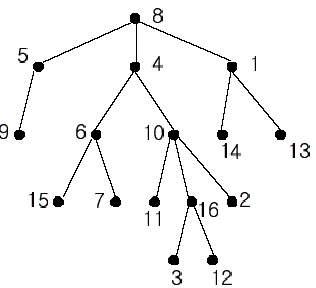
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
题目大意:给你一棵树,有N个结点,N-1条边。最后询问距离树上两个点(u,v)最近的
公共祖先是多少。
比如上图:6和16的最近公共祖先就是4;14和1的最近公共祖先就是1。
思路:对于最近公共祖先LCA问题,最经典的离线算法是Tarjan-LCA算法。用链式前向
星存储图和询问,Head[]和Edges[]表示图(树),QHead[]和QEdges[]表示询问。集合
的操作用并查集实现。这道题里用了indegree[]数组来存储结点的入度,找到入度为0的
根结点root,调用LCA(root)。
Tarjan-LCA算法:
对于每一点u:
1.建立以u为代表元素的集合。
2.遍历与u相连的节点v,如果没有被访问过,对于v使用Tarjan-LCA算法,结束后,将
v的集合并入u的集合。
3.对于与节点u相关的询问(u,v),如果v被访问过,则结果就是v所在集合的所代表的元
素。
参考:ACM-ICPC程序设计系列——图论及应用





















