
本教程的知识点为:深度学习介绍 1.1 深度学习与机器学习的区别 TensorFlow介绍 2.4 张量 2.4.1 张量(Tensor) 2.4.1.1 张量的类型 TensorFlow介绍 1.2 神经网络基础 1.2.1 Logistic回归 1.2.1.1 Logistic回归 TensorFlow介绍 总结 每日作业 神经网络与tf.keras 1.3 神经网络基础 神经网络与tf.keras 1.3 Tensorflow实现神经网络 1.3.1 TensorFlow keras介绍 1.3.2 案例:实现多层神经网络进行时装分类 神经网络与tf.keras 1.4 深层神经网络 为什么使用深层网络 1.4.1 深层神经网络表示 卷积神经网络 3.1 卷积神经网络(CNN)原理 为什么需要卷积神经网络 原因之一:图像特征数量对神经网络效果压力 卷积神经网络 3.1 卷积神经网络(CNN)原理 为什么需要卷积神经网络 原因之一:图像特征数量对神经网络效果压力 卷积神经网络 2.2案例:CIFAR100类别分类 2.2.1 CIFAR100数据集介绍 2.2.2 API 使用 卷积神经网络 2.4 BN与神经网络调优 2.4.1 神经网络调优 2.4.1.1 调参技巧 卷积神经网络 2.4 经典分类网络结构 2.4.1 LeNet-5解析 2.4.1.1 网络结构 卷积神经网络 2.5 CNN网络实战技巧 2.5.1 迁移学习(Transfer Learning) 2.5.1.1 介绍 卷积神经网络 总结 每日作业 商品物体检测项目介绍 1.1 项目演示 商品物体检测项目介绍 3.4 Fast R-CNN 3.4.1 Fast R-CNN 3.4.1.1 RoI pooling YOLO与SSD 4.3 案例:SSD进行物体检测 4.3.1 案例效果 4.3.2 案例需求 商品检测数据集训练 5.2 标注数据读取与存储 5.2.1 案例:xml读取本地文件存储到pkl 5.2.1.1 解析结构
完整笔记资料代码:https://gitee.com/yinuo112/AI/tree/master/深度学习/嘿马深度学习笔记/note.md
感兴趣的小伙伴可以自取哦~
全套教程部分目录:


部分文件图片:

卷积神经网络
3.1 卷积神经网络(CNN)原理
学习目标
-
目标
- 了解卷积神经网络的构成
- 记忆卷积的原理以及计算过程
- 了解池化的作用以及计算过程
-
应用
- 无
为什么需要卷积神经网络
在计算机视觉领域,通常要做的就是指用机器程序替代人眼对目标图像进行识别等。那么神经网络也好还是卷积神经网络其实都是上个世纪就有的算法,只是近些年来电脑的计算能力已非当年的那种计算水平,同时现在的训练数据很多,于是神经网络的相关算法又重新流行起来,因此卷积神经网络也一样流行。
- 1974年,Paul Werbos提出了误差反向传导来训练人工神经网络,使得训练多层神经网络成为可能。
- 1979年,Kunihiko Fukushima(福岛邦彦),提出了Neocognitron, 卷积、池化的概念基本形成。
- 1986年,Geoffrey Hinton与人合著了一篇论文:Learning representations by back-propagation errors。
- 1989年,Yann LeCun提出了一种用反向传导进行更新的卷积神经网络,称为LeNet。
- 1998年,Yann LeCun改进了原来的卷积网络,LeNet-5。
原因之一:图像特征数量对神经网络效果压力
假设下图是一图片大小为28 * 28 的黑白图片时候,每一个像素点只有一个值(单通道)。那么总的数值个数为 784个特征。

那现在这张图片是彩色的,那么彩色图片由RGB三通道组成,也就意味着总的数值有28 28 3 = 2352个值。

从上面我们得到一张图片的输入是2352个特征值,即神经网路当中与若干个神经元连接,假设第一个隐层是10个神经元,那么也就是23520个权重参数。
如果图片再大一些呢,假设图片为1000 1000 3,那么总共有3百万数值,同样接入10个神经元,那么就是3千万个权重参数。这样的参数大小,神经网络参数更新需要大量的计算不说,也很难达到更好的效果,大家就不倾向于使用多层神经网络了。
所以就有了卷积神经网络的流行,那么卷积神经网络为什么大家会选择它。那么先来介绍感受野以及边缘检测的概念。
注:另有卷积网络感受野的概念,也是为什么使用卷积的原因
3.1.1 卷积神经网络的组成
-
定义
- 卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比,卷积神经网络在图像等方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他浅层或深度神经网络,卷积神经网络需要考量的参数更少,使之成为一种颇具吸引力的深度学习结构。
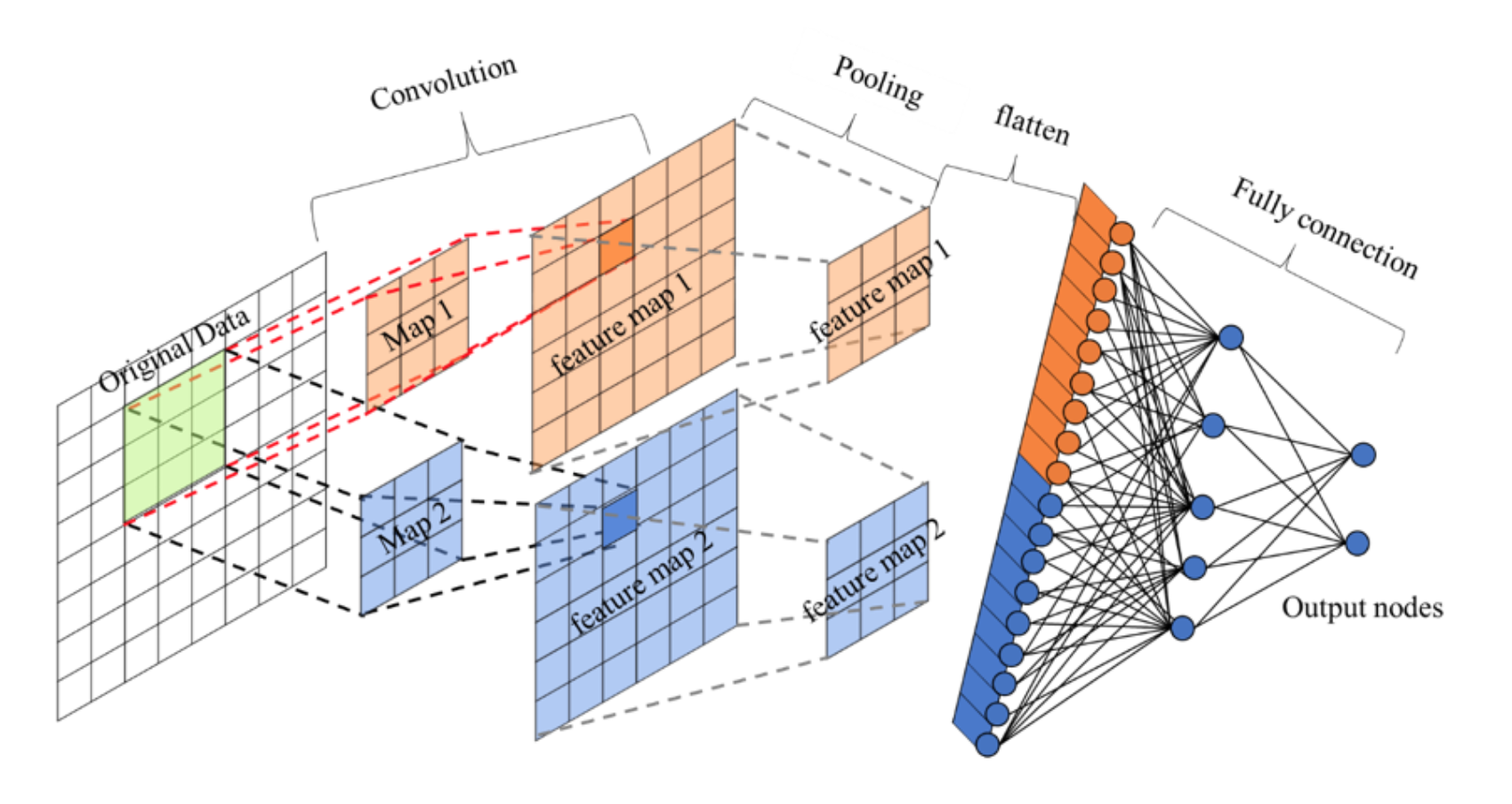
我们来看一下卷积网络的整体结构什么样子。
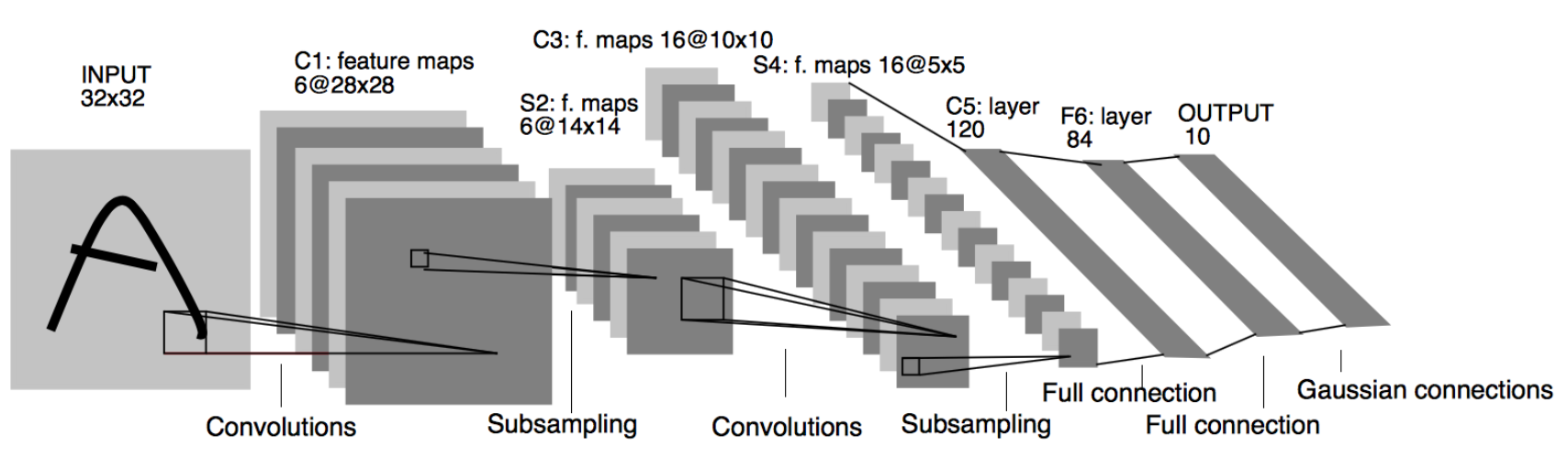
其中包含了几个主要结构
- 卷积层(Convolutions)
- 池化层(Subsampling)
- 全连接层(Full connection)
- 激活函数
3.1.2 卷积层
-
目的
- 卷积运算的目的是提取输入的不同特征,某些卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网路能从低级特征中迭代提取更复杂的特征。
-
参数:
- size:卷积核/过滤器大小,选择有1 1, 3 3, 5 * 5(为什么是奇数个)
- padding:零填充,Valid 与Same
- stride:步长,通常默认为1
-
计算公式

3.1.2.1 卷积运算过程
对于之前介绍的卷积运算过程,我们用一张动图来表示更好理解些。一下计算中,假设图片长宽相等,设为N
- 一个步长,3 X 3 卷积核运算
假设是一张5 X 5 的单通道图片,通过使用3 X 3 大小的卷积核运算得到一个 3 X 3大小的运算结果(图片像素数值仅供参考)

我们会发现进行卷积之后的图片变小了,假设N为图片大小,F为卷积核大小
相当于<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>N</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>=</mo><mn>5</mn><mo>−</mo><mn>3</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>3</mn></mrow><annotation encoding="application/x-tex">N - F + 1 = 5 - 3 + 1 = 3</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.68333em;"></span><span class="strut bottom" style="height:0.76666em;vertical-align:-0.08333em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">5</span><span class="mbin">−</span><span class="mord mathrm">3</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">3</span></span></span></span>
如果我们换一个卷积核大小或者加入很多层卷积之后,图像可能最后就变成了1 X 1 大小,这不是我们希望看到的结果。并且对于原始图片当中的边缘像素来说,只计算了一遍,二对于中间的像素会有很多次过滤器与之计算,这样导致对边缘信息的丢失。
-
缺点
- 图像变小
- 边缘信息丢失
3.1.3 padding-零填充
零填充:在图片像素的最外层加上若干层0值,若一层,记做p =1。
- 为什么增加的是0?
因为0在权重乘积和运算中对最终结果不造成影响,也就避免了图片增加了额外的干扰信息。

这张图中,还是移动一个像素,并且外面增加了一层0。那么最终计算结果我们可以这样用公式来计算:
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mn>5</mn><mo>+</mo><mn>2</mn><mo>∗</mo><mi>p</mi><mo>−</mo><mn>3</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>5</mn></mrow><annotation encoding="application/x-tex">5 + 2 * p - 3 + 1 = 5</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.64444em;"></span><span class="strut bottom" style="height:0.8388800000000001em;vertical-align:-0.19444em;"></span><span class="base textstyle uncramped"><span class="mord mathrm">5</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mbin">∗</span><span class="mord mathit">p</span><span class="mbin">−</span><span class="mord mathrm">3</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">5</span></span></span></span>
P为1,那么最终特征结果为5。实际上我们可以填充更多的像素,假设为2层,则
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mn>5</mn><mo>+</mo><mn>2</mn><mo>∗</mo><mn>2</mn><mo>−</mo><mn>3</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>7</mn></mrow><annotation encoding="application/x-tex">5 + 2 * 2 - 3 + 1 = 7</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.64444em;"></span><span class="strut bottom" style="height:0.72777em;vertical-align:-0.08333em;"></span><span class="base textstyle uncramped"><span class="mord mathrm">5</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mbin">∗</span><span class="mord mathrm">2</span><span class="mbin">−</span><span class="mord mathrm">3</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">7</span></span></span></span>,这样得到的观察特征大小比之前图片大小还大。所以我们对于零填充会有一些选择,该填充多少?
3.1.3.1 Valid and Same卷积
有两种两种形式,所以为了避免上述情况,大家选择都是Same这种填充卷积计算方式
-
Valid :不填充,也就是最终大小为
- <span class="katex"><span class="katex-mathml"><math><semantics><mrow><mo>(</mo><mi>N</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>)</mo><mo>∗</mo><mo>(</mo><mi>N</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow><annotation encoding="application/x-tex">(N - F + 1) * (N - F + 1)</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.75em;"></span><span class="strut bottom" style="height:1em;vertical-align:-0.25em;"></span><span class="base textstyle uncramped"><span class="mopen">(</span><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span><span class="mbin">∗</span><span class="mopen">(</span><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span></span></span></span>
-
Same:输出大小与原图大小一致,那么<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>N</mi></mrow><annotation encoding="application/x-tex">N</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.68333em;"></span><span class="strut bottom" style="height:0.68333em;vertical-align:0em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10903em;">N</span></span></span></span>变成了<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi></mrow><annotation encoding="application/x-tex">N + 2P</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.68333em;"></span><span class="strut bottom" style="height:0.76666em;vertical-align:-0.08333em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mord mathit" style="margin-right:0.13889em;">P</span></span></span></span>
- <span class="katex"><span class="katex-mathml"><math><semantics><mrow><mo>(</mo><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>)</mo><mo>∗</mo><mo>(</mo><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>)</mo></mrow><annotation encoding="application/x-tex">(N + 2P - F + 1) * (N + 2P - F + 1)</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.75em;"></span><span class="strut bottom" style="height:1em;vertical-align:-0.25em;"></span><span class="base textstyle uncramped"><span class="mopen">(</span><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span><span class="mbin">∗</span><span class="mopen">(</span><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span></span></span></span>
那也就意味着,之前大小与之后的大小一样,得出下面的等式
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mo>(</mo><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>)</mo><mo>=</mo><mi>N</mi></mrow><annotation encoding="application/x-tex">(N + 2P - F + 1) = N</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.75em;"></span><span class="strut bottom" style="height:1em;vertical-align:-0.25em;"></span><span class="base textstyle uncramped"><span class="mopen">(</span><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span><span class="mrel">=</span><span class="mord mathit" style="margin-right:0.10903em;">N</span></span></span></span>
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>P</mi><mo>=</mo><mfrac><mrow><mi>F</mi><mo>−</mo><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><annotation encoding="application/x-tex">P = \frac{F -1}{2}</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.872331em;"></span><span class="strut bottom" style="height:1.217331em;vertical-align:-0.345em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mrel">=</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathrm mtight">2</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span><span class="mbin mtight">−</span><span class="mord mathrm mtight">1</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span></span></span></span>
所以当知道了卷积核的大小之后,就可以得出要填充多少层像素。
3.1.3.2 奇数维度的过滤器
通过上面的式子,如果F不是奇数而是偶数个,那么最终计算结果不是一个整数,造成0.5,1.5.....这种情况,这样填充不均匀,所以也就是为什么卷积核默认都去使用奇数维度大小
-
1 1,3 3, 5 5,7 7
-
另一个解释角度
- 奇数维度的过滤器有中心,便于指出过滤器的位置
当然这个都是一些假设的原因,最终原因还是在F对于计算结果的影响。所以通常选择奇数维度的过滤器,是大家约定成俗的结果,可能也是基于大量实验奇数能得出更好的结果。
3.1.4 stride-步长
以上例子中我们看到的都是每次移动一个像素步长的结果,如果将这个步长修改为2,3,那结果如何?

这样如果以原来的计算公式,那么结果
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi><mo>+</mo><mn>1</mn><mo>=</mo><mn>6</mn><mo>+</mo><mn>0</mn><mo>−</mo><mn>3</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>4</mn></mrow><annotation encoding="application/x-tex">N + 2P - F + 1 = 6 + 0 -3 +1 = 4</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.68333em;"></span><span class="strut bottom" style="height:0.76666em;vertical-align:-0.08333em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10903em;">N</span><span class="mbin">+</span><span class="mord mathrm">2</span><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mbin">−</span><span class="mord mathit" style="margin-right:0.13889em;">F</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">6</span><span class="mbin">+</span><span class="mord mathrm">0</span><span class="mbin">−</span><span class="mord mathrm">3</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">4</span></span></span></span>
但是移动2个像素才得出一个结果,所以公式变为
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mfrac><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>+</mo><mn>1</mn><mo>=</mo><mn>1</mn><mi mathvariant="normal">.</mi><mn>5</mn><mo>+</mo><mn>1</mn><mo>=</mo><mn>2</mn><mi mathvariant="normal">.</mi><mn>5</mn></mrow><annotation encoding="application/x-tex">\frac{N + 2P - F}{2} + 1 = 1.5 + 1 = 2.5</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.872331em;"></span><span class="strut bottom" style="height:1.217331em;vertical-align:-0.345em;"></span><span class="base textstyle uncramped"><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathrm mtight">2</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span><span class="mbin mtight">+</span><span class="mord mathrm mtight">2</span><span class="mord mathit mtight" style="margin-right:0.13889em;">P</span><span class="mbin mtight">−</span><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">1</span><span class="mord mathrm">.</span><span class="mord mathrm">5</span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mrel">=</span><span class="mord mathrm">2</span><span class="mord mathrm">.</span><span class="mord mathrm">5</span></span></span></span>,如果相除不是整数的时候,向下取整,为2。这里并没有加上零填充。
所以最终的公式就为:
对于输入图片大小为N,过滤器大小为F,步长为S,零填充为P,
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mo>(</mo><mfrac><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi></mrow><mrow><mi>S</mi></mrow></mfrac><mo>+</mo><mn>1</mn><mo>)</mo><mo separator="true">,</mo><mo>(</mo><mfrac><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi></mrow><mrow><mi>S</mi></mrow></mfrac><mo>+</mo><mn>1</mn><mo>)</mo></mrow><annotation encoding="application/x-tex">(\frac{N + 2P - F}{S} + 1),(\frac{N + 2P - F}{S} + 1)</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.872331em;"></span><span class="strut bottom" style="height:1.217331em;vertical-align:-0.345em;"></span><span class="base textstyle uncramped"><span class="mopen">(</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathit mtight" style="margin-right:0.05764em;">S</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span><span class="mbin mtight">+</span><span class="mord mathrm mtight">2</span><span class="mord mathit mtight" style="margin-right:0.13889em;">P</span><span class="mbin mtight">−</span><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mopen">(</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathit mtight" style="margin-right:0.05764em;">S</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span><span class="mbin mtight">+</span><span class="mord mathrm mtight">2</span><span class="mord mathit mtight" style="margin-right:0.13889em;">P</span><span class="mbin mtight">−</span><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span></span></span></span>
3.1.5 多通道卷积
当输入有多个通道(channel)时(例如图片可以有 RGB 三个通道),卷积核需要拥有相同的channel数,每个卷积核 channel 与输入层的对应 channel 进行卷积,将每个 channel 的卷积结果按位相加得到最终的 Feature Map。
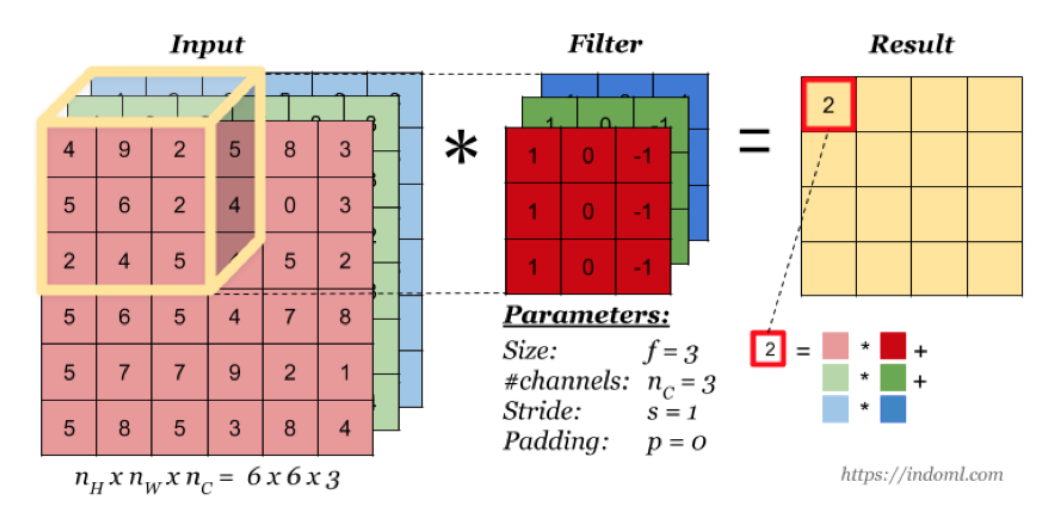
3.1.5.1 多卷积核(多个Filter)
当有多个卷积核时,可以学习到多种不同的特征,对应产生包含多个 channel 的 Feature Map, 例如上图有两个 filter,所以 output 有两个 channel。这里的多少个卷积核也可理解为多少个神经元。
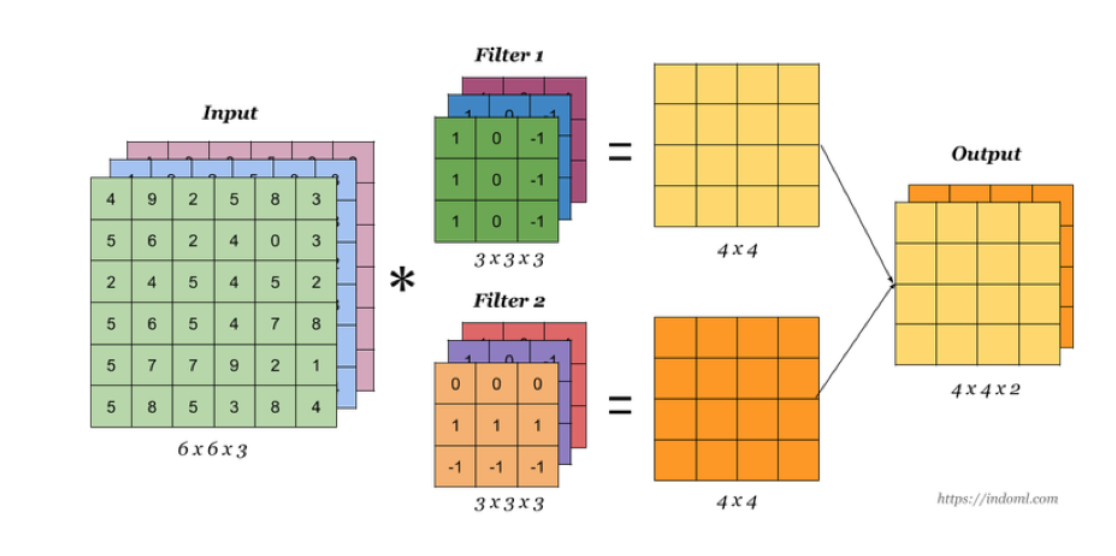
相当于我们把多个功能的卷积核的计算结果放在一起,能够检测到图片中不同的特征(边缘检测)
3.1.6 卷积总结
我们来通过一个例子看一下结算结果,以及参数的计算
- 假设我们有10 个Filter,每个Filter3 X 3 X 3(计算RGB图片),并且只有一层卷积,那么参数有多少?
计算:每个Filter参数个数为:3 3 3 + 1 bias = 28个权重参数,总共28 * 10 = 280个参数,即使图片任意大小,我们这层的参数也就这么多。
- 假设一张200 200 3的图片,进行刚才的FIlter,步长为1,最终为了保证最后输出的大小为200 * 200,需要设置多大的零填充
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mo>(</mo><mfrac><mrow><mi>N</mi><mo>+</mo><mn>2</mn><mi>P</mi><mo>−</mo><mi>F</mi></mrow><mrow><mi>s</mi></mrow></mfrac><mo>+</mo><mn>1</mn><mo>)</mo><mo>=</mo><mi>N</mi></mrow><annotation encoding="application/x-tex">(\frac{N + 2P - F}{s} + 1) = N</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.872331em;"></span><span class="strut bottom" style="height:1.217331em;vertical-align:-0.345em;"></span><span class="base textstyle uncramped"><span class="mopen">(</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathit mtight">s</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span><span class="mbin mtight">+</span><span class="mord mathrm mtight">2</span><span class="mord mathit mtight" style="margin-right:0.13889em;">P</span><span class="mbin mtight">−</span><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mbin">+</span><span class="mord mathrm">1</span><span class="mclose">)</span><span class="mrel">=</span><span class="mord mathit" style="margin-right:0.10903em;">N</span></span></span></span>
<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>P</mi><mo>=</mo><mfrac><mrow><mo>(</mo><mi>N</mi><mo>−</mo><mn>1</mn><mo>)</mo><mo>∗</mo><mi>s</mi><mo>+</mo><mi>F</mi><mo>−</mo><mi>N</mi></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mn>1</mn><mn>9</mn><mn>9</mn><mo>+</mo><mn>3</mn><mo>−</mo><mn>2</mn><mn>0</mn><mn>0</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>=</mo><mn>1</mn></mrow><annotation encoding="application/x-tex">P = \frac{(N -1) * s + F - N}{2} = \frac{199 + 3 - 200}{2} = 1</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:1.01em;"></span><span class="strut bottom" style="height:1.355em;vertical-align:-0.345em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.13889em;">P</span><span class="mrel">=</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathrm mtight">2</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.485em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mopen mtight">(</span><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span><span class="mbin mtight">−</span><span class="mord mathrm mtight">1</span><span class="mclose mtight">)</span><span class="mbin mtight">∗</span><span class="mord mathit mtight">s</span><span class="mbin mtight">+</span><span class="mord mathit mtight" style="margin-right:0.13889em;">F</span><span class="mbin mtight">−</span><span class="mord mathit mtight" style="margin-right:0.10903em;">N</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mrel">=</span><span class="mord reset-textstyle textstyle uncramped"><span class="mopen sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span><span class="mfrac"><span class="vlist"><span style="top:0.345em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle cramped mtight"><span class="mord scriptstyle cramped mtight"><span class="mord mathrm mtight">2</span></span></span></span><span style="top:-0.22999999999999998em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle textstyle uncramped frac-line"></span></span><span style="top:-0.394em;"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span><span class="reset-textstyle scriptstyle uncramped mtight"><span class="mord scriptstyle uncramped mtight"><span class="mord mathrm mtight">1</span><span class="mord mathrm mtight">9</span><span class="mord mathrm mtight">9</span><span class="mbin mtight">+</span><span class="mord mathrm mtight">3</span><span class="mbin mtight">−</span><span class="mord mathrm mtight">2</span><span class="mord mathrm mtight">0</span><span class="mord mathrm mtight">0</span></span></span></span><span class="baseline-fix"><span class="fontsize-ensurer reset-size5 size5"><span style="font-size:0em;"></span></span></span></span></span><span class="mclose sizing reset-size5 size5 reset-textstyle textstyle uncramped nulldelimiter"></span></span><span class="mrel">=</span><span class="mord mathrm">1</span></span></span></span>
卷积层充当特征提取的角色,但是并没有减少图片的特征数量,在最后的全连接层依然面临大量的参数,所以需要池化层进行特征数量的减少
3.1.7 池化层(Pooling)
池化层主要对卷积层学习到的特征图进行亚采样(subsampling)处理,主要由两种
- 最大池化:Max Pooling,取窗口内的最大值作为输出
- 平均池化:Avg Pooling,取窗口内的所有值的均值作为输出
意义在于:
- 降低了后续网络层的输入维度,缩减模型大小,提高计算速度
- 提高了Feature Map 的鲁棒性,防止过拟合

对于一个输入的图片,我们使用一个区域大小为2 2,步长为2的参数进行求最大值操作。同样池化也有一组参数,<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>f</mi><mo separator="true">,</mo><mi>s</mi></mrow><annotation encoding="application/x-tex">f, s</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.69444em;"></span><span class="strut bottom" style="height:0.8888799999999999em;vertical-align:-0.19444em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10764em;">f</span><span class="mpunct">,</span><span class="mord mathit">s</span></span></span></span>,得到2 2的大小。当然如果我们调整这个超参数,比如说3 * 3,那么结果就不一样了,通常选择默认都是<span class="katex"><span class="katex-mathml"><math><semantics><mrow><mi>f</mi><mo>=</mo><mn>2</mn><mo>∗</mo><mn>2</mn><mo separator="true">,</mo><mi>s</mi><mo>=</mo><mn>2</mn></mrow><annotation encoding="application/x-tex">f = 2 * 2, s = 2</annotation></semantics></math></span><span aria-hidden="true" class="katex-html"><span class="strut" style="height:0.69444em;"></span><span class="strut bottom" style="height:0.8888799999999999em;vertical-align:-0.19444em;"></span><span class="base textstyle uncramped"><span class="mord mathit" style="margin-right:0.10764em;">f</span><span class="mrel">=</span><span class="mord mathrm">2</span><span class="mbin">∗</span><span class="mord mathrm">2</span><span class="mpunct">,</span><span class="mord mathit">s</span><span class="mrel">=</span><span class="mord mathrm">2</span></span></span></span>
池化超参数特点:不需要进行学习,不像卷积通过梯度下降进行更新。
如果是平均池化则:
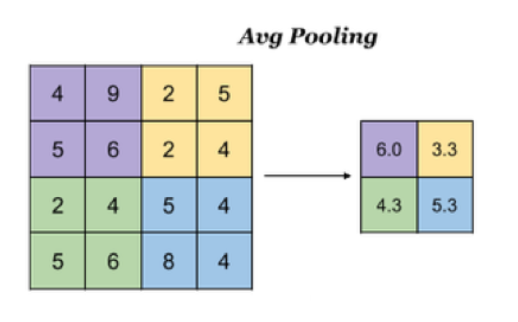
3.1.8 全连接层
卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层,而学习到的特征(Feature Map)最终应用于模型任务(分类、回归):
- 先对所有 Feature Map 进行扁平化(flatten, 即 reshape 成 1 x N 向量)
- 再接一个或多个全连接层,进行模型学习
3.1.9 总结
-
掌握卷积神经网路的组成
-
掌握卷积的计算过程
- 卷积过滤器个数
- 卷积过滤器大小
- 卷积过滤器步数
- 卷积过滤器零填充
-
掌握池化的计算过程原理























