岭回归如何进行异方差分析 岭回归的方差

一、一般线性回归遇到的问题

    在处理复杂的数据的回归问题时，普通的线性回归会遇到一些问题，主要表现在：

• 预测精度：这里要处理好这样一对为题，即样本的数量和特征的数量

• 时，最小二乘回归会有较小的方差
• 时，容易产生过拟合
• 时，最小二乘回归得不到有意义的结果

• 模型的解释能力：如果模型中的特征之间有相互关系，这样会增加模型的复杂程度，并且对整个模型的解释能力并没有提高，这时，我们就要进行特征选择。

以上的这些问题，主要就是表现在模型的方差和偏差问题上，这样的关系可以通过下图说明：

方差指的是模型之间的差异，而偏差指的是模型预测值和数据之间的差异。我们需要找到方差和偏差的折中。

二、岭回归的概念

    在进行特征选择时，一般有三种方式：

• 子集选择
• 收缩方式(Shrinkage method)，又称为正则化(Regularization)。主要包括岭回归个lasso回归。
• 维数缩减

    岭回归(Ridge Regression)是在平方误差的基础上增加正则项

,

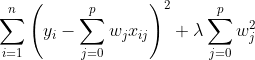
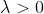
通过确定

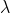
的值可以使得在方差和偏差之间达到平衡：随着

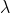
的增大，模型方差减小而偏差增大。    对

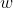
求导，结果为

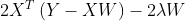
令其为0，可求得

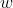
的值：

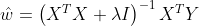
三、实验的过程

    我们去探讨一下取不同的

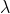
对整个模型的影响。

MATLAB代码

主函数

[plain] view plain copy

1. %% 岭回归(Ridge Regression)  
2.   
3. %导入数据  
4. data = load('abalone.txt');  
5. [m,n] = size(data);  
6.   
7. dataX = data(:,1:8);%特征  
8. dataY = data(:,9);%标签  
9.   
10. %标准化  
11. yMeans = mean(dataY);  
12. for i = 1:m  
13.     yMat(i,:) = dataY(i,:)-yMeans;  
14. end  
15.   
16. xMeans = mean(dataX);  
17. xVars = var(dataX);  
18. for i = 1:m  
19.     xMat(i,:) = (dataX(i,:) - xMeans)./xVars;  
20. end  
21.   
22. % 运算30次  
23. testNum = 30;  
24. weights = zeros(testNum, n-1);  
25. for i = 1:testNum  
26.     w = ridgeRegression(xMat, yMat, exp(i-10));  
27.     weights(i,:) = w';  
28. end  
29.   
30. % 画出随着参数lam  
31. hold on  
32. axis([-9 20 -1.0 2.5]);  
33. xlabel log(lam);  
34. ylabel weights;  
35. for i = 1:n-1  
36.     x = -9:20;  
37.     y(1,:) = weights(:,i)';  
38.     plot(x,y);  
39. end

岭回归求回归系数的函数

[plain] view plain copy

1. function [ w ] = ridgeRegression( x, y, lam )  
2.     xTx = x'*x;  
3.     [m,n] = size(xTx);  
4.     temp = xTx + eye(m,n)*lam;  
5.     if det(temp) == 0  
6.         disp('This matrix is singular, cannot do inverse');  
7.     end  
8.     w = temp^(-1)*x'*y;  
9. end