contains java 时间复杂度 java计算时间复杂度

算法的复杂度通常体现在时间复杂度和空间复杂度两个指标

下面主要说的是时间复杂度：

       算法时间复杂度的高低直接反映算法执行时间的长短，而算法的执行时间需要通过依据该算法编写的程序在计算机上执行所消耗的时间来度量。

      公式：

算法的执行时间 =

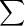
指令序列（i）的执行次数  *  指令序列(i)的执行时间

      算法的执行时间与指令序列的执行次数之和成正比。于是，尝试通过计算出依据算法编制的程序中每条语句的语句频度之和的值来估算一个算法的执行时间。所谓语句频度就是语句重复执行的次数

例如下列代码

public static void test(int[][] a, int[][] b, int[][] c, int n){
    for(int i=0; i<n; i++){                        // n+1
        for(int j=0; j<n; j++){                    // n(n+1)
            c[i][j] = 0;                           // n^2
            for(int k=0; k<n; k++){                // n^2(n+1)
                c[i][j] += a[i][j] * b[k][j];      // n^3
            }
        }
    }
}

说明：算法中每一条语句右边注释的内容为该语句的语句频度

解：时间复杂度为 T(n) = O(n^3)

 

最好、最坏和平均时间复杂度

   

最好时间复杂度：若待查找的数据元素恰好是数组中的第一个数据元素，只需比较一次即可找到，这算法的最好情况。

最坏时间复杂度：若待查找的数据袁术是最好一个元素，则需比较n次才能找到，这算法的最坏情况。

平均时间复杂度：若需要多次查找数据元素，并且以某种概率查找每个元素，在这种情况下，成功查找平均比较次数，这就是算法时间代价的平均情况。

 

       算法按时间复杂度分类

算法可按其执行时间分成两类：多项式时间算法    指数时间算法

多项式时间算法的时间复杂度由多种形式，其中最常见的形式如下：

（1）常量阶：O(1)

（2）线性阶：O(n)

（3）平方阶：O(n^2)

（4）立方阶：O(n^3)

（5）对数阶：O(log2 n)

（6）线性对数阶：O(nlog2 n)

指数时间算法的时间复杂度形式为O(a^n)，常见的有O(2^n)、O( n! )、O(n^n)