在做信号处理的时候,经常会对信号做自相关处理,比如对信号做功率估计,或者是参数拟合。在机器学习领域,如wule-walker方程也会遇到自相互函数的处理。
自相关矩阵百度百科的概念是:自相关矩阵就是,原矩阵是自己的相关矩阵。相关矩阵也叫相关系数矩阵,是由矩阵各列间的相关系数构成的。也就是说,相关矩阵第i行第j列的元素是原矩阵第i列和第j列的相关系数。
看完一头雾水。。。
然后看到这个博主写的觉得理解了一些。
自相关函数本质上来讲就是一个信号随时间变化的剧烈程度,但是对于无线长的信号,我们只能通过选取有限个测量信号做统计分析,来表示信号的变化程度,所以就用到了自相关函数。
自相关时一个信号于自身在不同时间点的互相关~
为啥就不同用均值和方差来表示呢?
1 自相关矩阵的基本概念
首先给出自相关函数的定义:
R(s,t)=E[(x(s)x(t))]
其中s,t是x(n)的不同时刻的信号值。
在实际的应用当中,我们把测得的数据一般是随机信号,比如说要测每天的10点,14点,20点的天气温度,测了N天以后,我们计算要10点x1温度的自相关函数。那么该怎么计算?
根据定义,我们需要知道x1和x2的概率密度f(x1,x2),然后通过来求
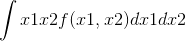
得x1和x2的自相关矩阵。显然,这个方法是行不通的。因为我们不知道f(x)的概率密度。但是我们又需要求出X1的自相关矩阵。
第二种方法就是测量无数天的10点温度和12点温度,然后带入R(s,t)做平均。显然这个方法也是行不通。因为这个方法所需要的数据是无穷的。
第三种方法就是假设每天10点和12点的温度是平稳随机过程。利用平稳随机过程的各态历经性,即时间平均收敛于集平均。
给出
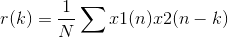
,其中k=s-t。n从0到N-1。
2 自相关矩阵的matlab实现
在matlab中,实现自相关的函数是xcorr()。
2.1 xcorr()

计算时先进行b的计算,用序列x中的元素的序号互相做减法,可以得到的所有值的可能集合,按照从小到大顺序排列后就得到了b;然后分别根据序号的“差”的情况计算序列a:
当b(1)=-2时,只有数据(1, 5)作差可以得到,即序号1和序号3的差,因此计算a(1)=1*5=5;
当b(2)=-1时,涉及到了序号对应的(3, 1)和序号(5, 3),所以计算a(2)=3*1+5*3=18;
当b(3)=0时,涉及到了序号对应的(1, 1), (3, 3)和(5, 5),因此计算a(3)=1*1+3*3+5*5=35;
当b(4)=1时,涉及到了序号对应的(3, 1)和(5, 3),计算a(4)=3*1+5*3=18;
当b(5)=2时,涉及到了序号对应的(5, 1)(后面的数据的序号减去前面数据的序号正好为2),计算a(5)=5*1=5
2.2 xcorr(x, 'unbiased')
参数'unbiased'的作用在于基于缺省参数时的计算结果,每个组的计算再除上该组的序号组数,比如b(1)时组数为1,记为N=1,则a(1)=1*5/N=5;b(2)时就是a(2)=18/N=18/2=9;类似等等;
点击(此处)折叠或打开
- >> [a, b] = xcorr(x, 'unbiased')
- a =
- 5.0000 9.0000 11.6667 9.0000 5.0000
- b =
- -2 -1 0 1 2
- >>
3. xcorr(x, 'biased')
参数'biased'的作用在于缺省参数的基础上除以序列x的长度,即a(1)=5/3;比如:
点击(此处)折叠或打开
1. >> [a, b] = xcorr(x, 'biased')
2.
3. a =
4.
5. 1.6667 6.0000 11.6667 6.0000 1.6667
6.
7.
8. b =
9.
10. -2 -1 0 1 2
11.
12. >>4. xcorr(x, 'coeff')
此时用于求序列x的自相关序列,其结果是针对'biased'的情况进行归一化,使得b=0时即中间的值a(3)=1,因此a(1)=5/11.6667,所有的分组数据在'biased'基础上都通过11.6667归一运算:
点击(此处)折叠或打开
1. >> [a, b] = xcorr(x, 'coeff')
2.
3. a =
4.
5. 0.1429 0.5143 1.0000 0.5143 0.1429
6.
7.
8. b =
9.
10. -2 -1 0 1 2
11.
12. >>
13.
3.编写函数实现xocrr函数
根据1中提到的第三种方法计算自相关函数。u是输入的数据
clear all;
u=[1 2 3 4];
for k=0:length(u)-1 %U的自相关函数,点数多的时候,计算速度慢等价于xcorr,biased
tmp = 0;
for i=1:length(u)-k
tmp = tmp + u(i)*u(i+k);
end
rx(k+1) = tmp/length(u);
end
得到结果为:

用matlab的函数xcorr()
clear all;
u=[1 2 3 4];
rx1=xcorr(u,'biased');
rx1=rx1(length(u):end)

可以得到
rx1=xcorr(u,'biased');
rx1=rx1(length(u):end)
才是我们用第三种方法所求的相关函数























