目录
遗传算法回顾
遗传算法回顾
1.遗传算法概述
遗传算法(Genetic Algorithm)是基于模拟达尔文生物进化论的自然选择和遗传学机理的生物过程计算模型，是一种通过模拟自然进化过程在样本空间搜索最优解的方法.
在这里给出几个觉得很不错的几篇介绍遗传算法有史以来最容易理解的遗传算法，莫凡进化算法，遗传算法的python实现
遗传算法关键词：基因编码 自然选择 遗传变异
2.遗传算法实现
在写代码前，先明确我们程序完成后的解决目标：能够快速寻找函数的最优解，留出函数接口用来解决拥有不同自变量的函数最优解求取．
①导入需要用到的库函数
#可以用来计算算法运行时间
import datetime
#用来绘图的神奇库
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
#数据运算，操作库
import numpy as np②先写出大致框架
class Ga_method():
def __init__(self,DNA_Size=32,Pop_size=200,
Crossover_rate=0.8,mutation_rate=0.005,
N_genrations=50,f,**kwargs):
pass
#基因解码 二进制->十进制
def translateDNA(self,pop):
pass
#得到适应度
def get_fitness(self,pop):#适应度函数
pass
#交叉和变异
def crossover_and_mutation(self,pop):
pass
#变异
def mutate(self,child):
pass
#选择
def select(self,pop,fitness):
pass
#打印算法的相关信息
def print_info(self,pop):
pass
#画出动态图
def plot_3d(self,ax):
pass
def plot_2d(self,ax):
pass
#训练 进化
def train(self):
pass③分析构造方法的各部分及实现
init:
作为构造方法，首先要确定构造一个对象需要用到那些数据及参数
设置种群规模Pop_size,并限制自变量的搜索范围**kwargs(为了适应不同数量的自变量范围)，迭代次数N_genration,目标函数f,以及染色体的交叉Crossover_rate和变异概率mutation_rate，和会影响解精度的染色体大小DNA_Size
Pop:二维数组（Pop_size*DNA_Size）即各体带有染色体大小为DNA_Size*n的群体,n代表的是自变量个数
f:方法对象，接受各自不同自变量的函数
class Ga_method():
def __init__(self,DNA_Size=32,Pop_size=200,
Crossover_rate=0.8,mutation_rate=0.005,
N_genrations=50,f=_3DF,**kwargs):
#X,Y范围
self.doom={}
for key,values in kwargs.items():
self.doom[key]=values
self.doom_num=len(self.doom)
#遗传算法超参数设置
self.DNA_S=DNA_Size
self.Pop_s=Pop_size
self.Cross_rate=Crossover_rate
self.mutate_rate=mutation_rate
self.generations=N_genrations
self.startTime=datetime.datetime.now()
self.F=f编码及解码方式：
在程序中我们以及设置了DNA_Size*n长度的二进制数组来表示个体的染色体即编码过程，如果要将其转化成为自变量则需要一个解码过程。
举一个具体的例子：
我们要求解的函数f(x,y)为 lst为自变量即 lst[0]表示x lst[1]表示y 在自变量范围为[-3,3]的最大值
def _3DF(lst):
return 3*(2-lst[0])**2*np.exp(-(lst[0]**2)-(lst[1]+10)**2)- 10*(lst[0]/5 - lst[0]**3 - lst[1]**5)*np.exp(-lst[0]**2-lst[1]**2)- 1/3**np.exp(-(lst[0]+1)**2 - lst[1]**2)根据参数设置DNA_Size=32,则随机生成的个体包含32*2个二进制数[0 1 1 1 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 0 1 0 1 1 1 0 0 0 1 1 0 0 0 1 0 0 0 0]，前32个二进制数表示的是x,后32个二进制数表示的是y，对应的十进制数为(x, y): (-0.005332557718579878,1.569111966660505)，二进制编码有利于遗传算法中交叉和变异操作，而十进制则是程序最后得出的结果，同时十进制数参与适应度函数的计算，如果是求取最大值的化，将xy的值代入函数f中，适应度越大则被选取为下一代的概率也就越高，这体现了适者生存的理念．绿色小点即为种群散布在目标函数中，并逐步向函数最大值移动求解函数的直观体现如下图
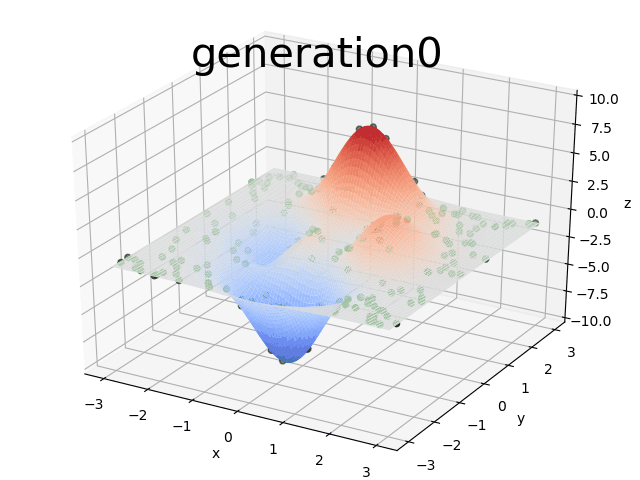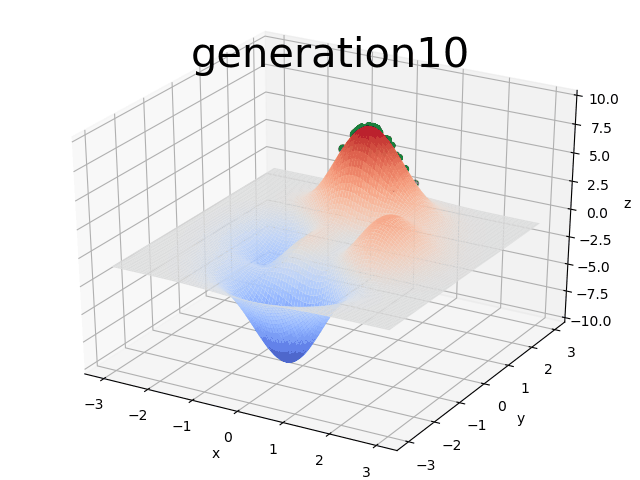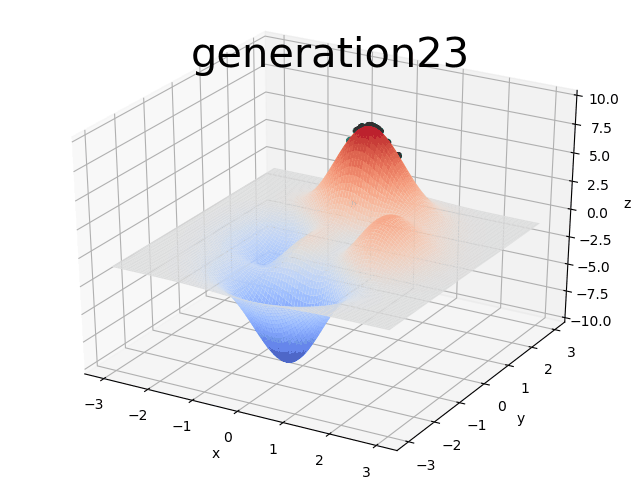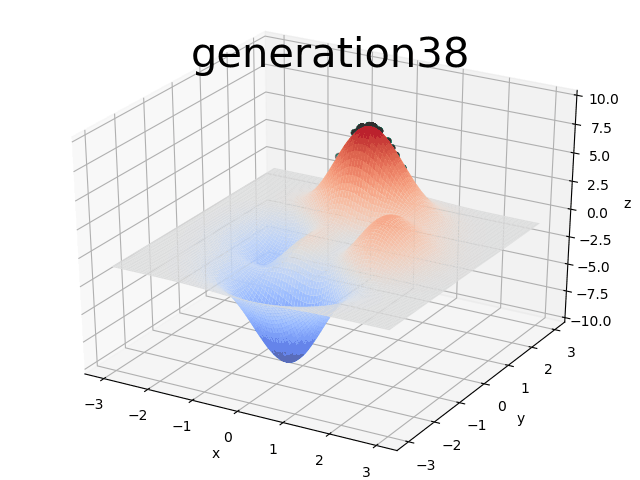
二进制转化为十进制即为解码过程：
10位二进制可以表示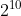
种不同的状态，可以看成是将最后要转化为的十进制区间x,y∈[−3,3](下面讨论都时转化到这个区间）切分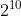
成份，显而易见，如果我们增加二进制串的长度，那么我们对区间的切分可以更加精细，转化后的十进制解也更加精确。例如，十位二进制全1按权展开为1023，最后映射到[-3, 3]区间时为3，而1111111110（前面9个1）按权展开为1022，1022/(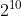
−1)≈0.9990221022，0.999022∗(3−(−3))+(−3)≈2.994134.
def translateDNA(self,pop):
pop_=[]
values=[]
for key,i in zip(self.doom,range(self.doom_num)):
pop_.append(pop[:,i*self.DNA_S:(i+1)*self.DNA_S])
values.append(pop_[-1].dot(2**np.arange(self.DNA_S)[::-1])/float(2**self.DNA_S-1)*(self.doom[key][1]-self.doom[key][0])+self.doom[key][0])
return values适应度和选择
根据初始化参数设置，我们拥有一个包含200个体的种群，并且对种群里面个体进行了解码操作，则可以将自变量代入f(x,y)中得到的数字作为个体的适应度，适应度越高表示被选取为下一代的个体概率也就越高．为了防止出现负的适应值，则可以各自适应度减去最小适应度作为适应值，遗传算法依据原则：适应度越高，被选择的机会越高，而适应度越低，被选择的机会越低
def get_fitness(self,pop):#适应度函数
variables= self.translateDNA(pop)
pred = self.F([variables[i] for i in range(len(variables))])
return(pred-np.min(pred))+1e-3
def select(self,pop,fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(self.Pop_s), size=self.Pop_s, replace=True,
p=(fitness)/(fitness.sum()) )np.random.choice(a,size,replace,p)#赌盘选取函数
a:代表参与的种群 size:表示随机选取后生成的种群规模 replace:是否放回 p:概率，其维度与a向对应
交叉．变异
通过选择来选取优秀的基因，并不是最好的基因，需要通过种群中的个体之间进行相互交叉和个体变异来产生比当前更好的基因．但是繁衍后代并不一定能够保证每次都会比上一代更加优秀，所以需要通过自然选择的力量来让能够真正适应环境（适应度高）的个体存活下来，进而让其参与下一次的繁衍后代中去．
具体的繁衍后代包含交叉和变异两步，交叉即从种群中选取父本和母本基因，通过随机选取基因交配点来生成交叉子代基因，交配点前的基因来自与父本基因，交配点后的基因来自与母本基因．而变异通常是将交叉子代中的某一基因发生随机改变，通常是直接改变DNA的一个二进制位(0-1).
交叉概率的选择能够保证有一部分父代优秀基因不参与繁衍行为直接进入下一轮，使得算法更加稳定．变异概率的选取是为了让算法能够跳出其局部最优解，但是如果变异概率越大，算法稳定性就会越差．
def crossover_and_mutation(self,pop):#交叉和变异
new_pop = []
for father in pop:
child = father
if np.random.rand() < self.Cross_rate:
mother = pop[np.random.randint(self.Pop_s)]
cross_points = np.random.randint(low=0, high=self.DNA_S*self.doom_num) #随机产生交叉的点
child[cross_points:] = mother[cross_points:]
self.mutate(child) #每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutate(self,child): #变异
if np.random.rand() < self.mutate_rate: #以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, self.DNA_S*self.doom_num) #随机产生一个实数，代表要变异基因的位置
child[mutate_point] = child[mutate_point]^1 #将变异点的二进制为反转上面涉及的所有遗传算法的核心模块，将这些模块在train主函数中迭代起来，让种群去进化
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #生成种群 matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS): #种群迭代进化N_GENERATIONS代
crossover_and_mutation(pop, CROSSOVER_RATE) #种群通过交叉变异产生后代
fitness = get_fitness(pop) #对种群中的每个个体进行评估
pop = select(pop, fitness) #选择生成新的种群
