前言
大家好,我是来自于「华为」的「程序员小熊」。今天给大家带来一道与「数组」相关的题目,这道题同时也是字节、微软和亚马逊等互联网大厂的面试题,即力扣上的第 88 题-合并两个有序数组。
本文主要介绍「逆向双指针」的策略来解答此题,供大家参考,希望对大家有所帮助。
合并两个有序数组

示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-10^9 <= nums1[i], nums2[i] <= 10^9解题思路
合并两个「有序」数组,比较容易想到的策略主要有以下几种:
为了方便描述,假设长度更长的数组为 nums1,长度稍微短一点的数组为 nums2,下文也是一直遵循这种描述。
策略一:将 nums2 中的元素全部插入到 nums1 的尾部,然后对处理之后的 nums1 进行排序。
策略二:双指针法,先开辟一个新数组,长度为两个数组的长度之和,然后让两个指针分别指向两个数组的头部,比较这个两个指针指向的数组元素的值,将数值较小的放到新数组的头部,再将指向的数值较小的指针右移,继续比较,直到遍历完其中一个数组即可。
「复杂度分析」
【时间复杂度】:策略一是「O((n + m)lg(n + m))」,主要是合并之后再排序的时间复杂度;策略二是「O(n + m)」,主要是遍历两个数组的时间复杂度。
【空间复杂度】:策略一是「O(1)」,未开辟额外的存储空间;策略二是「O(n + m)」,额外开辟了长度为 m + n 的数组。
逆向双指针
从前面的分析可知,策略二相对于策略一来说,时间复杂度「更优」了,但开辟了「额外」的空间。
有没有方法能够将策略二的空间复杂度优化呢?答案是有的,由于题目明确告知了「可以假设 nums1 的空间大小等于 m + n」,因此可以利用这个条件将策略二的空间复杂度优化。具体如下栗子分析:
「举例」
假设 nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3,如下图示。

按照题目要求,合并后的数组应该如下图示:

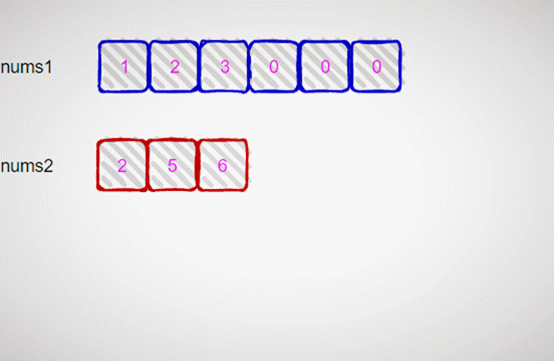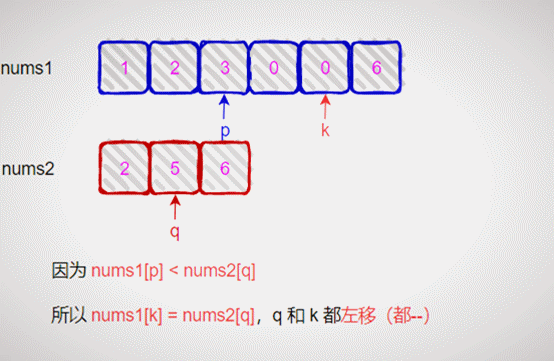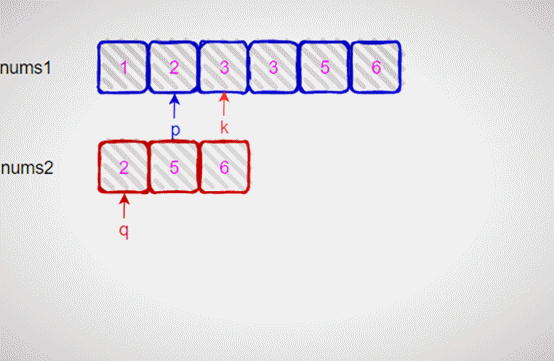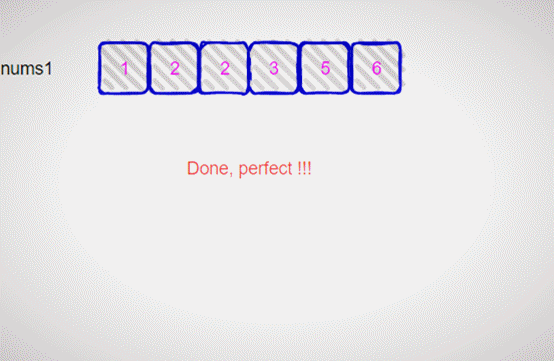
先设置两个指针 p 和 q,分别指向两个数组的末尾,假设 k 为 两数组的长度,如下图示:

比较 p 和 q 指向数组位置的元素值

将元素值较大的存放在 nums1[k] 中,并左移 k 和 q(指向的数值较大的指针)

以此类推,其处理的完整过程如下动图示
Show me the Code
「C」
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
int p = m - 1; // p 指向 nums1[m - 1]
int q = n - 1; // q 指向 nums2[n - 1]
int k = m + n - 1; // k 指向 nums1[m + n - 1]
/* nums1、nums2 其中一个未遍历完,不断比较 nums1[p] 和 nums1[q],更新 nums[k] */
while (p >= 0 && q >= 0) {
nums1[k--] = nums1[p] > nums2[q] ? nums1[p--] : nums2[q--];
}
/* 若 n > m,nums1 遍历完成,将 nums2 中尚未遍历完的元素拷贝到 nums1 中 */
while (q >= 0) {
nums1[k--] = nums2[q--];
}
}「C++」
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p = m - 1;
int q = n - 1;
int k = nums1.size() - 1;
while (p >= 0 && q >= 0) {
nums1[k--] = nums1[p] > nums2[q] ? nums1[p--] : nums2[q--];
}
while (q >= 0) {
nums1[k--] = nums2[q--];
}
}「Java」
void merge(int[] nums1, int m, int[] nums2, int n) {
int p = m - 1;
int q = n - 1;
int k = nums1.length - 1;
while (p >= 0 && q >= 0) {
nums1[k--] = nums1[p] > nums2[q] ? nums1[p--] : nums2[q--];
}
while (q >= 0) {
nums1[k--] = nums2[q--];
}
}「Python3」
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
p, q, k = m - 1, n - 1, len(nums1) - 1
while p >= 0 and q >= 0:
if nums1[p] > nums2[q]:
nums1[k] = nums1[p]
p -= 1
else:
nums1[k] = nums2[q]
q -= 1
k -= 1
while q >= 0:
nums1[k] = nums2[q]
q -= 1
k -= 1「Golang」
func merge(nums1 []int, m int, nums2 []int, n int) {
p, q, k := m - 1, n - 1, len(nums1) - 1
for p >= 0 && q >= 0 {
if nums1[p] > nums2[q] {
nums1[k] = nums1[p]
p -= 1
} else {
nums1[k] = nums2[q]
q -= 1
}
k -= 1
}
for q >= 0 {
nums1[k] = nums2[q]
q -= 1
k -= 1
}
}「复杂度分析」
时间复杂度:「O(n + m)」,需要遍历一遍两个数组。
空间复杂度:「O(1)」,未开辟额外的空间。





















