灰度共生矩阵python 灰度共生矩阵matlab

上周五在复现一篇论文（"Visual-Salience-Based Tone Mapping for High Dynamic Range Images"）中的算法时涉足到了基于灰度共生矩阵的显著性度量，便顺手给实现了以下。我们将共生关系定义在w*w的窗口内，窗口内的不同两个像素p、q为共生关系，其灰度

、

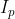
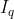
即为共生灰度。论文算法在计算灰度共生矩阵前会先将灰度值量化为K个等级。当共生关系的考察窗口半径为r时，对于每个像素，我们只需要考察它右下方(包含本行和本列)的(r+1)*(r+1)-1个像素。因为站在当前像素p角度去考察左上方像素q等同于从像素q角度去考察右下角像素p，所以没有必要考察另外3个子分区（以当前像素为原点将窗口划为4个分区的话）。

下面将代码贴出来与大家分享：

function M=ICH(img,K,r)
%求灰度共生矩阵程序
%K为量化等级
%r为衡量共生性质的邻域半径，灰度m,n在(2r+1,2r+1)的窗口内同时出现过即视为共生
if ~exist('K','var')
    K=255;
end
if ~exist('r','var')
    r=4;
end
interval=(max(img(:))-min(img(:)))/(K-0.5);
Q=floor((img-min(img(:)))/interval)+1;
rowNum=size(Q,1);
M=zeros(K,K);
idxShift=zeros(r+1,r+1); %参考像素相对于当前像素的索引偏移量
for i=0:r
    for j=0:r
        idxShift(i+1,j+1)=i+j*rowNum;
    end
end
idxShift=idxShift(:);
for p=2:length(idxShift) %idxShift(1)为0，表示当前进行统计的两像素实际为同一像素，跳过
    for i=1:size(Q,1)-r
        for j=1:size(Q,2)-r
            idx=(j-1)*rowNum+i;
            s=idxShift(p);
            M(Q(idx),Q(idx+s))=M(Q(idx),Q(idx+s))+1;
            M(Q(idx+s),Q(idx))=M(Q(idx+s),Q(idx))+1;
        end
    end
end

脚本文件：

img=rgb2gray(imread('onion.png'));
K=255;
r=4;
M=ICH(img,K,r);
nM=M/sum(M(:)); %归一化
figure,imshow(10*nM/max(nM(:)));

r=4的输出结果为：

r=10的输出结果为：

可以看出，这种基于灰度共生矩阵的显著性度量计算复杂度是正比于窗口半径（实际是半径加1）的平方的，对于r=4的情况，每个点需要考察24个共生点。而基于最小方向对比度的显著性度量由于利用了积分图优化，每个像素点的计算复杂度是O(1)量级，只需要进行几次加减、乘方和开方运算，从计算复杂度而言更低，所以可以考虑采用基于最小方向对比度的显著性度量来替代基于灰度共生矩阵的显著性度量来减少计算量。当然啦，具体效果还需要实验后才能评价。