在搜索树的大家族里,红黑树算是用途最广泛的一个代表了。在我们使用的C++STL库中,set、map都是以它作为底层去实现的。当然在一些其他的地方,比如Java集合中的TreeSet和TreeMap,还有Linux虚拟内存的管理,也是通过红黑树去实现的。所以,今天我们来分析一下红黑树是怎样实现的。
红黑树是一棵二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是Red或Black。通过对任何一条从根到叶子简单 路径上的颜色来约束,红黑树保证最长路径不超过最短路径的两倍,因而近似于平衡。
所以我们就把满足下面性质的二叉搜索树称为红黑树:
1. 每个节点不是红色就是黑色
2. 根节点是黑色的
3. 如果有一个节点是红的,那么它的子节点一定是黑的(不存在连续的红节点)
4. 每条路径下存在相同数目的黑节点
5. 每个叶子(NIL)节点是黑色的(这是的叶子节点指的是为(NIL/NULL)的叶子结点)
1.插入
红黑树的插入情况是比较多的,最开始创建一个红黑树,它的根节点一定是黑,插入的第二个节点为了满足黑色节点数目相同的性质,肯定是红的,以此类推,当节点较多时我们可以将插入情况分为以下几类:
第一种:祖父节点是黑的,父亲和叔叔节点是红的,现在我们插入一个cur红节点(方框节点可存在,可不存在)

分析:这个时候,这棵红黑树已经不满足性质“不存在连续红节点”,所以这个时候需要对树进行调整。这种情况我们可以直接将父亲和叔叔节点的颜色进行改变为黑色,改变后又满足了红黑树的性质。

第二种:祖父节点是黑的,父亲节点是红的,叔叔节点不存在或者是黑色的,此时cur红节点(方框节点可存在,可不存在)

分析:同理,这种情况也不满足黑色节点数量相同这一性质。这个时候简单的改变颜色肯定不能解决问题,在这种情况下往往是因为cur子节点的调整,引起上面节点也需要调整。所以这个时候,我们需要对这棵树进行旋转。

第三种:祖父节点是黑的,父亲节点是红的,叔叔节点不存在或者是黑色的,此时cur红节点是父亲的右孩子(方框节点可存在,可不存在)

分析:现在对树做调整,可能情况会比较复杂,如果我们把cur节点变成父亲的左孩子,那剩下的问题就和第二种情况一样了。所以我们对父亲子树进行右旋即可。

pair<Node*, bool> Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new Node(key, value);
_root->_color = BLACK;
return make_pair(_root, true);
}
Node* parent = NULL;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
return make_pair(cur,false);
}
cur = new Node(key, value);
if (parent->_key > key)
parent->_left = cur;
else
parent->_right = cur;
cur->_parent = parent;
while (parent && parent->_color == RED)
{
Node* grandfather = parent->_parent; //1.判断父亲和叔叔的关系
if (parent == grandfather->_left) //父亲在左,叔叔在右
{
Node* uncle = grandfather->_right; //2.判断叔叔的情况
if (uncle != NULL && uncle->_color == RED) //a.叔叔存在且为红 -> 变色
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandfather->_color = RED;
cur = grandfather;
parent = cur->_parent;
}
else //b.叔叔不存在或者叔叔为黑
{
if (cur == parent->_right)
{
RotateL(parent);
swap(cur, parent);
}
RotateR(grandfather);
parent->_color = BLACK;
grandfather->_color = RED;
break;
}
}
else //叔叔在左,父亲在右
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_color == RED) //叔叔存在且为红 ,变色
{
parent->_color = BLACK;
uncle->_color = BLACK;
grandfather->_color = RED;
cur = grandfather;
parent = cur->_parent;
}
else //叔叔不存在或为黑
{
if (cur == parent->_left)
{
RotateR(parent);
swap(cur, parent);
}
RotateL(grandfather);
parent->_color = BLACK;
grandfather->_color = RED;
break;
}
}
}
_root->_color = BLACK;
return make_pair(_root, true);
}总结:关于红黑树的插入,我们是从插入的节点开始,依次向上调整,直到这棵树的节点符合红黑树的性质。
2.红黑树的左右旋
对于左右旋这个概念,其实在学习查找树这一个系列的时候并不陌生,很多时候树的插入问题,我们都会用到这个方法来使它达到一种平衡。
对红黑树也是如此。首先,我们借助一个动画来看看右旋是怎么个旋法。
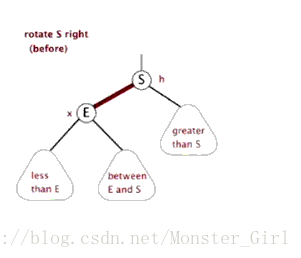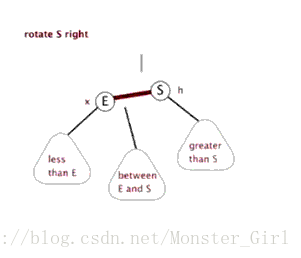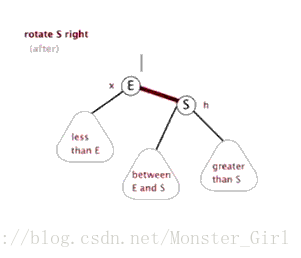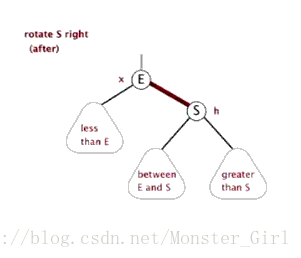
根据这个动画再去实现,就比较容易了。代码实现如下。
void RotateR(Node* parent) //右旋
{
assert(parent);
Node* child = parent->_left;
Node* grandfather = parent->_parent;
Node* Rchild = child->_right;
if (Rchild)
Rchild->_parent =parent ;
parent->_left = Rchild;
parent->_parent = child;
child->_right = parent;
if (grandfather == NULL)
{
child->_parent = NULL;
_root = child;
}
else
{
if (grandfather->_left == parent)
grandfather->_left = child;
else
grandfather->_right = child;
child->_parent = grandfather;
}
}同理,左旋的实现也可以借助动画来理解。
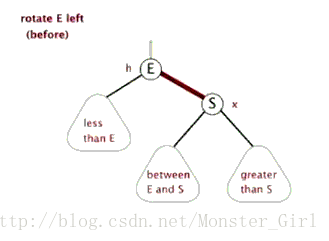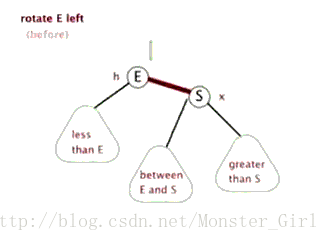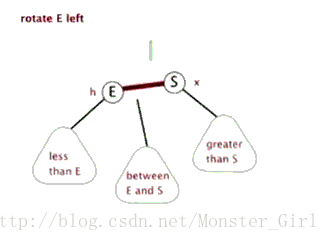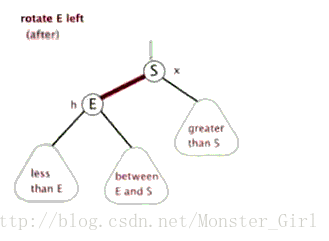
void RotateL(Node* parent) //左旋
{
assert(parent);
Node* child = parent->_right;
Node* Lchild = child->_left;
Node* grandfather = parent->_parent;
if (Lchild)
Lchild->_parent = parent;
parent->_right = Lchild;
parent->_parent = child;
child->_left = parent;
if (grandfather == NULL)
{
_root = child;
child->_parent = NULL;
}
else
{
if (parent == grandfather->_left)
grandfather->_left = child;
else
grandfather->_right = child;
child->_parent = grandfather;
}
}总结:在查找树中,合理的使用左右旋会使整个问题化繁为简。
3.如何判断当前的红黑树是红黑树
在我们完成插入算法后,这个时候就有了一个新问题,我们如何判断一棵树是不是没有问题的红黑树?要解决这个问题,就得从红黑树的性质入手了。
1. 如果根节点是红的,肯定不是红黑树;
2. 如果有连续的红节点,肯定不是红黑树;
3. 如果黑色节点的路径长度不一样,肯定不是红黑树。
这三条性质就够我们去判断一个树是不是红黑树了。第一二条性质比好判断,如何实现第三个?这时候我们就需要去任意路径count一次黑色节点的路径长度,然后再用这个长度和每一条路径的长度进行比较,只要有一条路径不一样,那就可以直接得出这不是一颗红黑树了。直到判断到每一条路径的叶子节点后,它都相等,那么此时这个性质就满足了。
bool IsBalance()
{
if (_root == NULL) return true;
if (_root->_color == RED) return false;
int BlackNum = 0; //统计一条路径的黑色节点数量
Node* left = _root;
while (left)
{
if (left->_color == BLACK)
BlackNum++;
left = left->_left;
}
int count = 0;
return _IsBalance(_root,BlackNum,count);
}
bool _IsBalance(Node* root, const int BlackNum, int count)
{
if (root == NULL) return true;
if (root->_color == RED && root->_parent->_color == RED)
{
cout << "存在连续红节点" << endl;
return false;
}
if (root->_color == BLACK)
++count;
if (root->_left == NULL && root->_right == NULL)
{
if (count != BlackNum)
{
cout << "黑节点数目不同" << endl;
return false;
}
else
return true;
}
return _IsBalance(root->_left, BlackNum, count) && _IsBalance(root->_right, BlackNum, count);
}其实,相对比其他查找树,红黑树的查找时间复杂度一直控制在 O(lgn),这就要求它一直处于近似平衡状态。也正是因为这一点,红黑树是一种非常高效的平衡查找树,所以在很多语言的内部都会或多或少使用它来作为底层实现。





















