红黑树 删除节点 java java红黑树数据结构

红黑树首先是一个平衡二叉树，但是它不是完美的平衡二叉树。让一棵二叉查找树在动态插入的过程中保持平衡需要的代价比较高，红黑树是为此产生的。

1. 红黑树的性质

1. 每个节点只能是红色或者是黑色；
2. 根节点必须是黑色；
3. 每个叶子节点是黑色，注意，这里叶子节点指末端空节点；
4. 如果一个节点是红色，那么它的子节点必然是黑色，这意味着不存在两个连续的红色节点；
5. 从一个节点到该节点的子孙节点的所有路径上包含相同数量的黑节点。

以上是红黑树的5点基本性质。

2. 红黑树的基本定义

public class RBTree<T extends Comparable<T>> {

    private RBTNode<T> mRoot;    // 根结点

    private static final boolean RED   = false;
    private static final boolean BLACK = true;

    public class RBTNode<T extends Comparable<T>> {
        boolean color;        // 颜色
        T key;                // 关键字(键值)
        RBTNode<T> left;    // 左孩子
        RBTNode<T> right;    // 右孩子
        RBTNode<T> parent;    // 父结点

        public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

    }

    ...
}

3.红黑树的基本操作

3.1 旋转

我们依然需要依靠旋转、重新着色等操作使得树能够保持红黑树的性质。

3.1.1 左旋转

先上一张gif

Java实现

private void leftRotate(RBTNode<T> x){
	//x的右孩子节点赋值给y
	RBTNode<T> y=x.right;
	//将y的左孩子节点赋值给x的右孩子
	//如果y的左孩子为非空，将x设置为y的左孩子的父亲
	x.right=y.left;
	if(y.left!=null){
		y.left.parent=x;
	}
	y.parent=x.parent;
	//如果x的父亲为null，则将y设置为根节点
	if(x.parent==null){
		this.mRoot=y;
	}else{
		if(x.parent.left==null)
			x.parent.left=y;
		else
			x.parent.right=y;
	}
	//将x设置为y的左孩子
	y.left=x;
	//将x的父亲设置为y
	x.parent=y;
}

3.1.2 右旋转

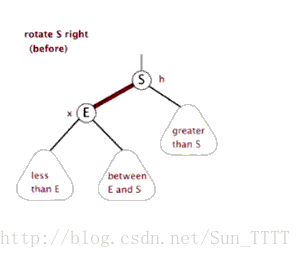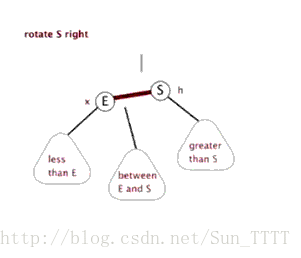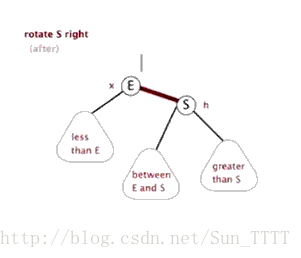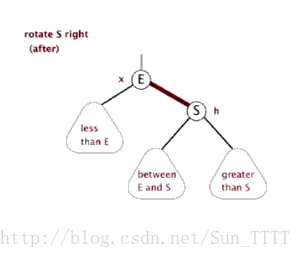
Java实现

private void rightRotate(RBTNode<T> y){
	//y的左孩子节点赋值给x
	RBTNode<T> x=y.left;
	//将x的右孩子节点设置为y的左孩子节点
	//如果x的右孩子为非空，则将y设置为x的右孩子的父亲
	y.left=x.right;
	if(x.right!=null){
		x.right.parent=y;
	}
	x.parent=y.parent;
	//如果y的父节点为空，则将x设置为根节点
	if(y.parent==null){
		this.mRoot=x;
	}else{
		if(y.parent.left==null)
			y.parent.left=x;
		else
			y.parent.right=x;
	}
	//将y设置为x的右孩子
	x.right=y;
	//将x设置为y的父亲
	y.parent=x;
}

3.2 插入节点

插入节点的操作可以分为三步来完成：

1. 将红黑树视为一个普通的二叉查找树，然后向该查找树插入节点；
2. 将插入的节点颜色置为红色；
3. 通过重新上色、旋转等操作使得树重新符合红黑树的基本性质。

public void insert(RBTNode<T> node){
	int cmp;
	RBTNode<T> y=null;
	RBTNode<T> x=node;
	//将红黑树当做一棵二叉查找树，进行插入操作
	while(x!=null){
		y=x;
		cmp=node.key.compareTo(x.key);
		if(cmp<0)
			x=x.left;
		else
			x=x.right;
	}
	node.parent=y;
	if(y!=null){
		cmp=node.key.compareTo(y.key);
		if(cmp<0)
			y.left=node;
		else
			y.right=node;
	}else{
		this.mRoot=node;
	}
	//2.设置插入节点为红色
	node.color=RED;
	//3.调整树为红黑树
	insertFixUp(node);
}

以下是调整函数

public void insertFixUp(RBTNode<T> node){
	RBTNode<T> parent,gparent;
	//若父节点存在，且颜色为红色
	while(((parent=parentOf(node))!=null)&&isRed(parent)){
		gparent=parentOf(parent);
		//若父节点是祖父节点的左孩子
		if(parent==gparent.left){
			//case1:叔叔节点是红色
			RBTNode<T> uncle=gparent.right;
			if(uncle!=null&&isRed(uncle)){
				setBlack(uncle);
				setBlack(parent);
				setRed(gparent);
				node=gparent;
				continue;
			}
			//case2:叔叔节点是黑色，且当前节点是右孩子
			if(parent.right==node){
				RBTNode<T> tmp;
				leftRotate(parent);
				tmp=parent;
				parent=node;
				node=tmp;
			}
			//case3:叔叔节点是黑色，当前节点是左孩子
			setBlack(parent);
			setRed(gparent);
			rightRotate(gparent);
		}else{
			//父节点是祖父节点的右孩子
			RBTNode<T> uncle=parent.left;
			//case1:叔叔节点是红色
			if(uncle!=null&&isRed(uncle)){
				setBlack(uncle);
				setBlack(parent);
				setRed(gparent);
				node=gparent;
				continue;
			}
			//case2:叔叔节点是黑色，当前节点是左孩子
			if(parent.left==node){
				RBTNode<T> tmp;
				rightRotate(parent);
				tmp=parent;
				parent=node;
				node=tmp;
			}
			//case3:叔叔节点是黑色，当前节点是右孩子
			setBlack(parent);
			setRed(gparent);
			leftRotate(gparent);
		}
	}
	setBlack(this.mRoot);
}

public RBTNode<T> parentOf(RBTNode<T> node){
	return node.parent;
}

public boolean isRed(RBTNode<T> node){
	return node.color==RED;
}

public void setBlack(RBTNode<T> node){
	node.color=BLACK;
}

public void setRed(RBTNode<T> node){
	node.colpr=RED;
}