python 高斯分布采样值 高斯分布的检验

基于统计学的方法

掌握关于高斯分布的异常检测

一元高斯分布

高斯分布也称正态分布， 我们可以利用已有的数据来预测总体中的  和 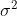 的计算方法如下：

概率密度函数为：

选定一个参数ε，将P(x)=ε作为我们的判定边界，当P(x)>ε时预测数据为正常数据，否则为异常。

多元高斯分布

构建协方差矩阵，使用所有特征来构建p（x）

首先我们先计算所有特征的平均值及协方差矩阵：

多元高斯分布的概率密度为

协方差？

通俗地讲, 协方差可以理解为：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？
你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。
你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。
从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

非参数的方法

建立直方图

1.根据输入数据来构造一个直方图，可是多元也可以是一元

2.对照直方图来检验他。

HBOS算法

假设数据集所有维度是独立的，每个维度有一定的区间，密度越大，有异常点的可能性越低。

算法流程

1.为每个数据维度建立直方图，值就是其相对频率

*静态直方图，构建k个等宽的箱子

*动态直方图，对所有样本的值进行排序，然后固定数量n/k个连续值落入箱子中，宽度就由第一个值和最后一个值决定，所有箱子的面积是一样的

2.对每个维度都计算了一个独立的直方图，其中每个箱子的高度表示密度的估计。然后为了使得最大高度为1（确保了每个特征与异常值得分的权重相等），对直方图进行归一化处理。最后，每一个实例的HBOS值由以下公式计算：

练习

使用PyOD库生成toy example并调用HBOS

导入所需要的库

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib.font_manager
from pyod.models.abod import ABOD
from pyod.models.knn import KNN

创建一个有异常值的随机数据集

from pyod.utils.data import generate_data, get_outliers_inliers

#生成具有两个特征
X_train, Y_train = generate_data(n_train=200,train_only=True, n_features=2)

# 默认情况下，生成数据函数中的outlier_fraction为0.1 
outlier_fraction = 0.1

# 将这两个值存储在不同的numpy数组中
x_outliers, x_inliers = get_outliers_inliers(X_train,Y_train)

n_inliers = len(x_inliers)
n_outliers = len(x_outliers)

#分离两个特征并用它来绘制数据 
F1 = X_train[:,[0]].reshape(-1,1)
F2 = X_train[:,[1]].reshape(-1,1)

# 创建meshgrid 
xx , yy = np.meshgrid(np.linspace(-10, 10, 200), np.linspace(-10, 10, 200))

# 绘制散点图 
plt.scatter(F1,F2)
plt.xlabel('F1')
plt.ylabel('F2')

创建dictionary并添加用于检查异常值的模型

classifiers = {
     'Angle-based Outlier Detector (ABOD)'   : ABOD(contamination=outlier_fraction),
     'K Nearest Neighbors (KNN)' :  KNN(contamination=outlier_fraction)
}

使数据适合我们在字典中添加的每个模型，然后查看每个模型如何检测离群值：

#设置图形大小
plt.figure(figsize=(10, 10))

for i, (clf_name,clf) in enumerate(classifiers.items()) :
    # 使数据适合模型
    clf.fit(X_train)

    # 预测原始异常
    scores_pred = clf.decision_function(X_train)*-1

    # 预测数据点类别
    y_pred = clf.predict(X_train)

    # 预测中没有错误
    n_errors = (y_pred != Y_train).sum()
    print('No of Errors : ',clf_name, n_errors)

    # 以下代码是创建可视化

    # threshold考虑数据点的inlier或者outlier
    threshold = stats.scoreatpercentile(scores_pred,100 *outlier_fraction)

    # decision function计算每个点的原始异常分数
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) * -1
    Z = Z.reshape(xx.shape)

    subplot = plt.subplot(1, 2, i + 1)

    # 设定最小值到threshold value，填充蓝色
    subplot.contourf(xx, yy, Z, levels = np.linspace(Z.min(), threshold, 10),cmap=plt.cm.Blues_r)

    # 异常值等于threshold的部分，填充红色
    a = subplot.contour(xx, yy, Z, levels=[threshold],linewidths=2, colors='red')

    # 填充橙色等高线，其中异常得分的范围是从threshold到最大异常得分
    subplot.contourf(xx, yy, Z, levels=[threshold, Z.max()],colors='orange')

    # inliers为白点的散点图
    b = subplot.scatter(X_train[:-n_inliers, 0], X_train[:-n_inliers, 1], c='white',s=20, edgecolor='k') 
    # outliers为黑点的散点图
    c = subplot.scatter(X_train[-n_outliers:, 0], X_train[-n_outliers:, 1], c='black',s=20, edgecolor='k')
    subplot.axis('tight')

    subplot.legend(
        [a.collections[0], b, c],
        ['learned decision function', 'true inliers', 'true outliers'],
        prop=matplotlib.font_manager.FontProperties(size=10),
        loc='lower right')

    subplot.set_title(clf_name)
    subplot.set_xlim((-10, 10))
    subplot.set_ylim((-10, 10))
plt.show()