什么是卷积
首先看卷积公式
y(t)=f(t)∗g(t)=∫∞−∞f(u)g(t−u)du
它是通过两个函数 f(t) 和 g(t) 来生成第三个函数的一种数学算子。从负无穷到正无穷遍历全部 u 值,把 g(t-u) 的值乘以 f(u) 的值之后再进行累加,得到关于该累加操作的关于 t 的函数。从另一个角度看,卷积就是一种加权求和。
用离散信号方便理解卷积的操作。有两个函数f(n)和g(n),分别如下:


则卷积运算f(n)*g(n)过程为,
首先,f(n)乘以g(0),g(0)为1,则

其次,f(n)乘以g(1)并整个右移一个单位,g(1)为2,则

接着,f(n)乘以g(2)并整个右移一个单位,g(2)为2,则

同样,f(n)乘以g(3)并整个右移一个单位,g(3)为3,则

最后,将4个图叠加即完成卷积运算。

所以卷积就是一个函数在另一个函数的加权叠加。它是一种加权求和。
对于二维卷积,对应的公式为:
C(x,y)=∫∞−∞∫∞−∞f(t,u)g(x−t,y−u)dtdu
离散公式为:
C(x,y)=∑∞t=−∞∑∞u=−∞f(t,u)g(x−t,y−u)
二维卷积的运算过程中涉及到 f(t,u) 函数矩阵的180度翻转,而卷积神经网络的卷积运算则稍微有点不同,运算过程不进行180度翻转,且g在前f在后。
从卷积神经网络来看,f(x,y) 可看成是2*2 或 3*3的网格,即卷积核,而 g(x,y) 则对应图像的像素,比如28*28,则卷积操作其实就是卷积核 f 在图像 g 上一格格移动而做的乘积并累加和。详细的操作后面会有形象说明。
神经网络
了解卷积神经网络之前需先了解最基础的BP神经网络,BP神经网络一般如下图所示,有多个层,比如左边的包含输入层、隐层和输出层,而右边的则包含了两个隐层。每层的神经元与下一神经元全互连,同层之间的神经元不会相连,输入层用于接收输入,经过隐层加工后再到输出层加工并输出。

BP神经网络好的地方就是我们完全不必事先考虑怎么用数学方程来描述输入和输出之间的关系,转而考虑的是设计一个N层神经网络,而要多少层、每层要多少个节点就可以我们根据经验来设计,可通过不同的网络模型来看哪个模型能更好地拟合。
BP神经网络其实很直观很好理解,整个过程如下。
下面是一个三层(不算输入层)神经网络,两个输入经过几层网络后得到一个输出。
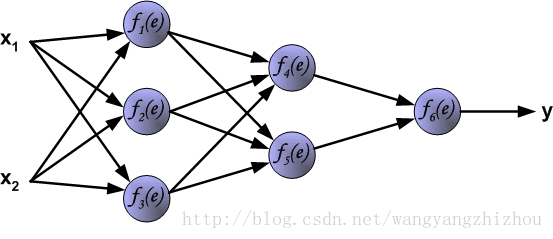
x1、x2,f1(e)节点对应的权重为w(x1)1、w(x2)1,则有y1=f1(w(x1)1+w(x2)1)。

f2(e)节点对应的权重为w(x1)2、w(x2)2,则有y2=f2(w(x1)2+w(x2)2)。
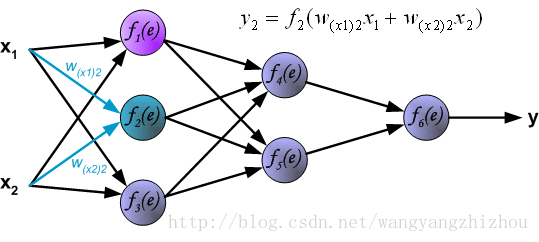
f3(e)节点对应的权重为w(x1)3、w(x2)3,则有y3=f3(w(x1)3+w(x2)3)。
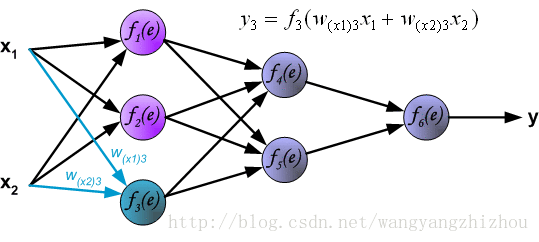
y1、y2、y3,对应权重为w14 w24 w34,则y4=f4(w14y1+w24y2+w34y3)。
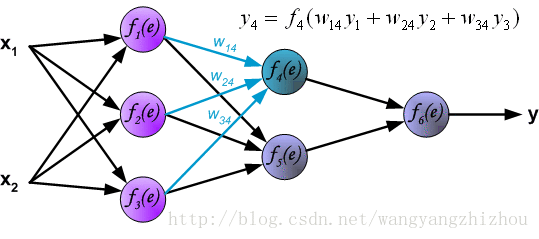
f5(e)对应的权重为w15 w25 w35,则y5=f5(w15y1+w25y2+w35y3)。
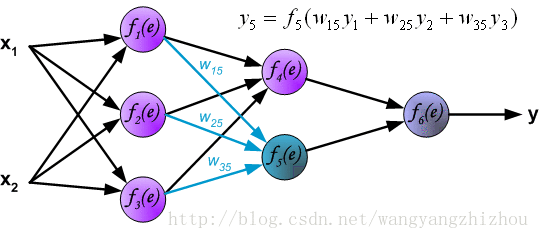
y4和 y5,假设权重分别为w46 w56,则y6=f6(w46y4+w56y5)。

卷积神经网络
可以看到上面的BP神经网络层与层之间都是全连接的,对于图像处理领域,当神经网络处理大图像时,全连接会导致待训练的参数非常庞大,比如100万个像素的图像,对于100个节点的隐层,则会产生亿级别的参数,如果更多层及更多个节点那参数数量将会无比庞大。BP神经网络没有假设相邻图像之间存在紧密联系。综上所述,BP神经网络不适合做图像处理。
为减少参数数量,首先想到可以构建部分连接的神经网络,每个神经元不再与上层所有神经元相连,而是连接某部分。另外还能通过权值共享来减少参数数量,一组连接共享权重而不必每个连接权重都不同。除此之外,还能通过池化来减少每层的样本数,从而减少参数数量。结合以上特点,卷积神经网络就是这样的一种网络。
看一个卷积神经网络示意图,它包含了若干卷积层、池化层和全连接层。图像输入经过第一层卷积层处理后,得到4层feature,为什么可以是4层呢?其实就是可以自定义4个不同的filter对输入分别运算,就得到4层feature。然后池化层对卷积后的feature进行池化处理,得到更小的feature,这里运算后同样是4层feature。接着继续根据filter做卷积和池化处理,最后通过两个全连接层完成输出。

卷积层
前面说到卷积操作其实就是卷积核 f 在图像 g 上一格格移动而做的乘积并累加和,具体的操作如下两个图,g(x,y) 是一个5*5的图像,卷积核 f(x,y) 是3*3的网格。卷积核在图像上逐步移动计算乘积并累加,最后得到一个3*3的特征映射。

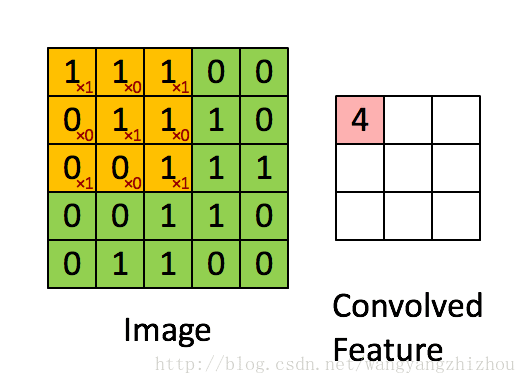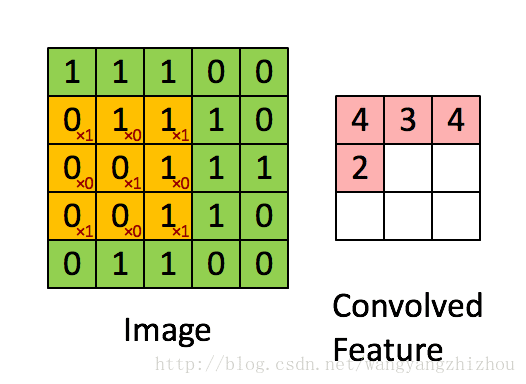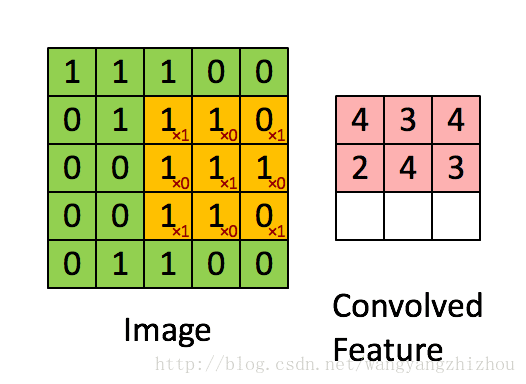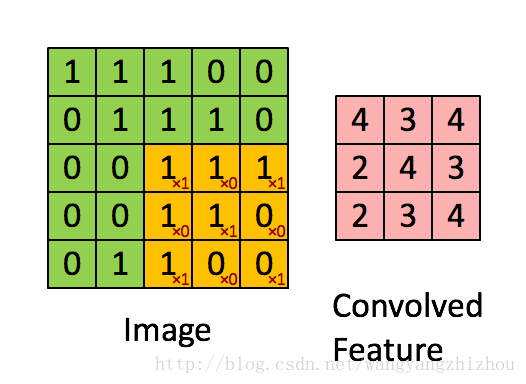
移动的步伐为1个单位,当然也可以2个单位地移动。而前面说到的卷积操作可以由多个filter进行运算,这时卷积运算是怎样进行的呢?下图形象地展示了整个过程,其中输入有3层的数据,再定义两个3*3*3的filter,分别为Filter W0 和Filter W1 ,Filter W0以2个单位移动,3个维度分别对应输入层做乘积累加运算得到3个结果,再将这3个结果加起来并加上偏移量b0得到最终结果。Filter W0遍历输入得到一个3*3的输出,同样地,Filter W1也是进行同样地操作得到另外一个3*3输出。最终的输出就是一个3*3*2的网络。
另外可以看到最外一圈都为0,这是一种处理边界的方式,叫zero padding,通过它不会让边缘的特性丢失。
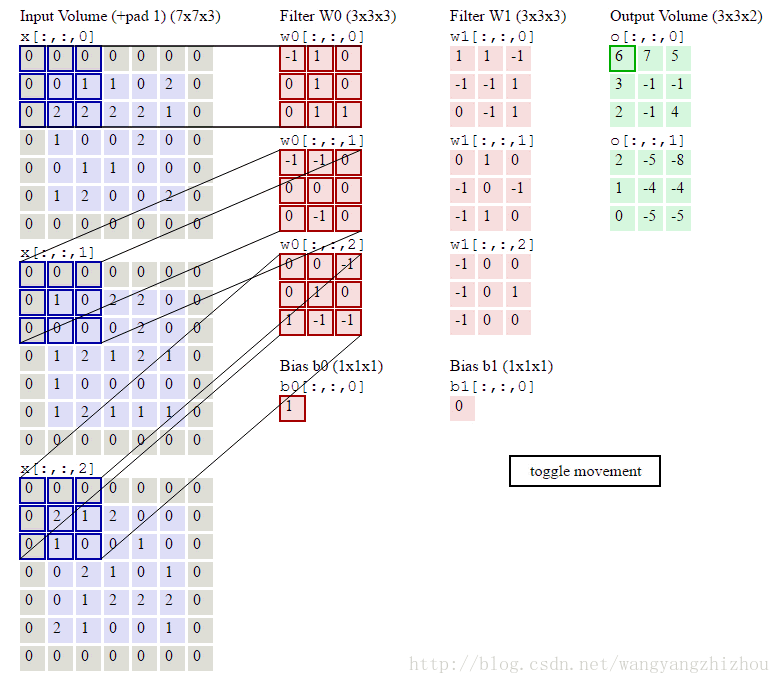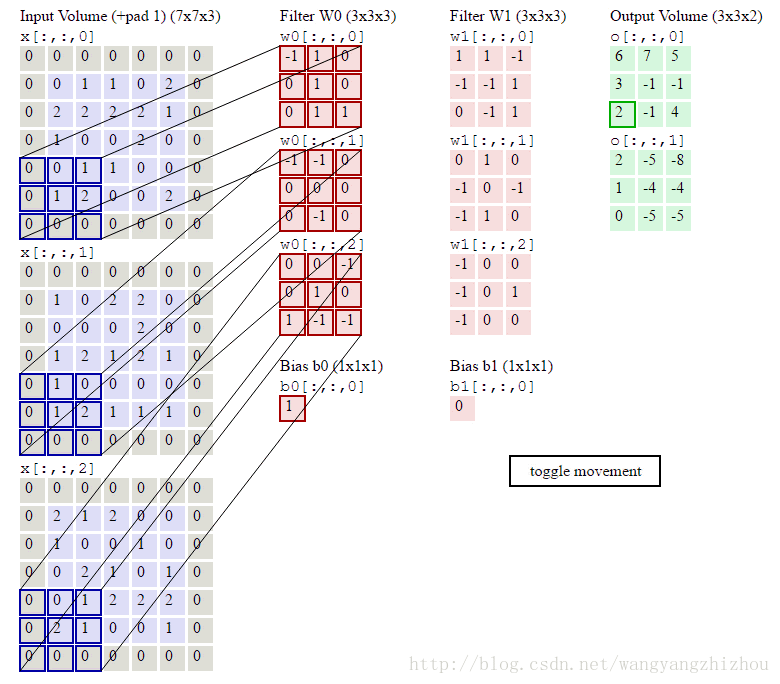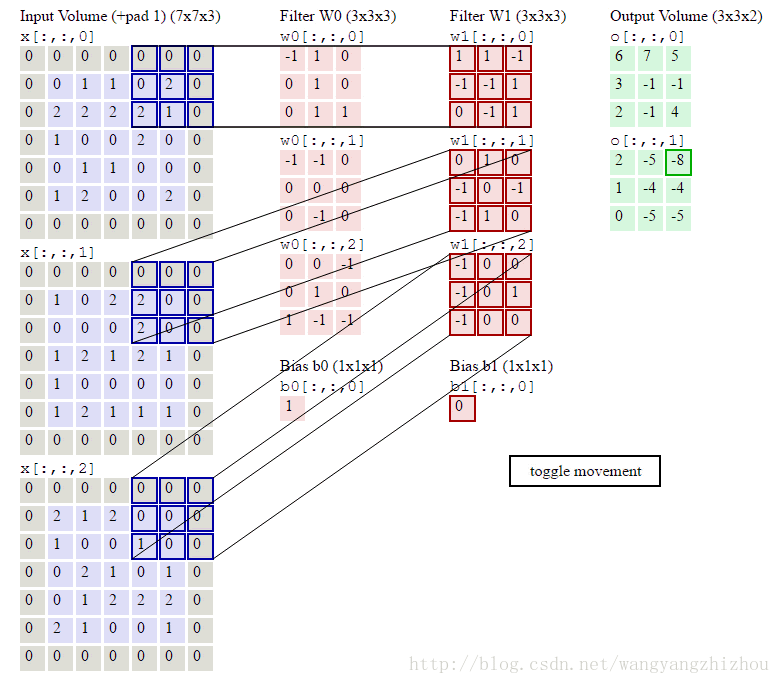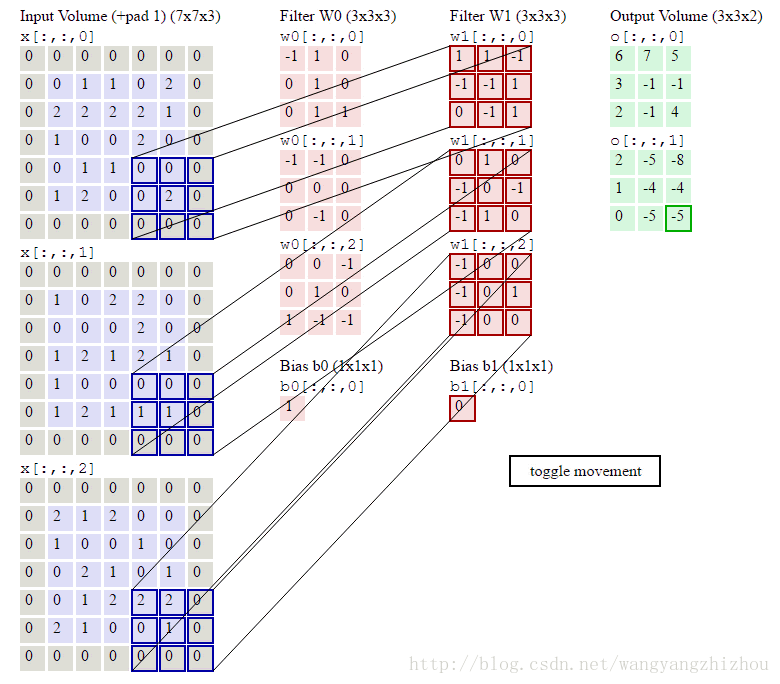
池化层
常见的池化有两种,最大值池化和平均值池化。最大值池化即在区域中选择最大值作为池化后的值,而平均值池化则是区域中所有值的平均值作为池化后的值。
它的思想可以看下图,卷积处理后特征还是具有较多神经元,通过池化抽样处理后减少了神经元。
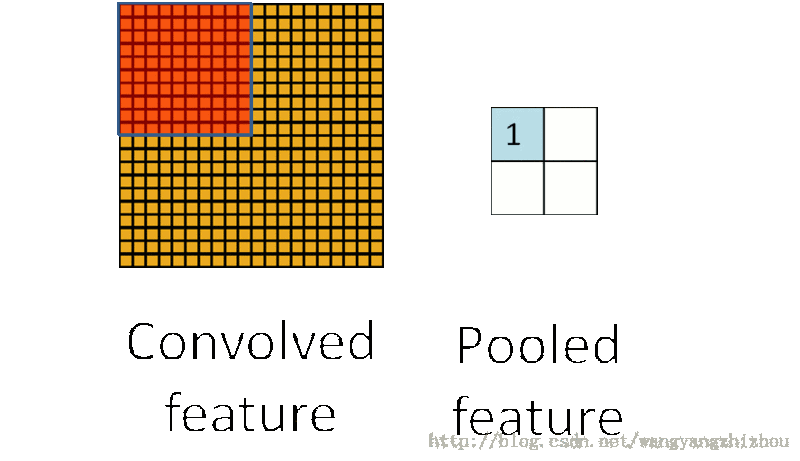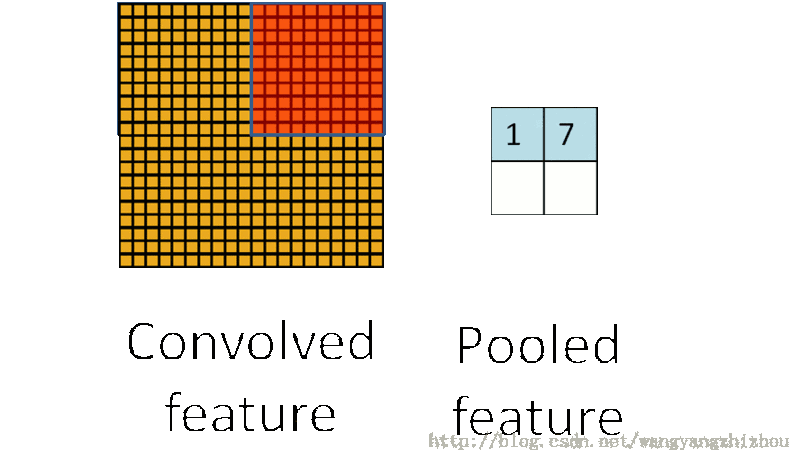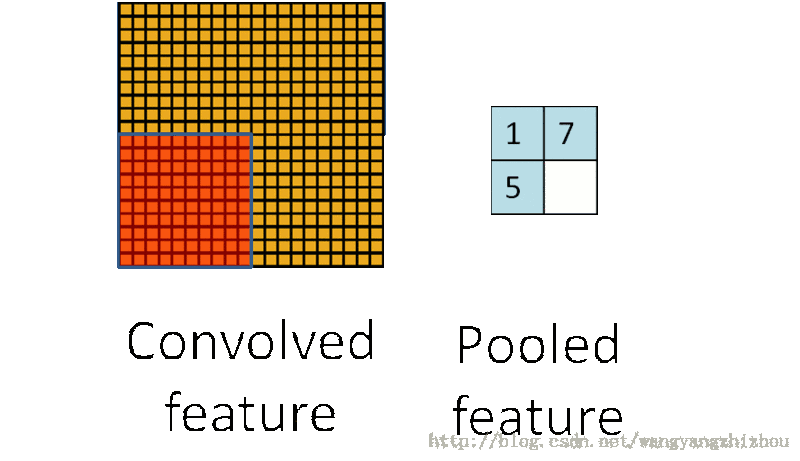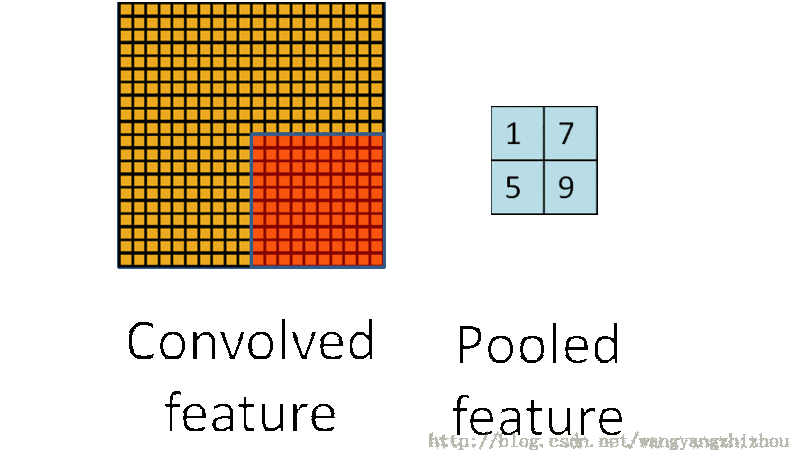
池化处理的好处就是能显著减少参数的数量,并且池化单元具有平移不变性。
全连接层
特征都提取好后将进入到一个全连接层,全连接层其实就像前面的经典的BP神经网络,经过多层卷积和池化层处理后参数已经大大减少,一般最后再通过添加 softmax 分类器实现最终的识别。
训练卷积神经网络
卷积神经网络的训练比全连接神经网络的训练复杂很多,因为全连接神经网络相邻两层的所有神经元都相连,而卷积神经网络则要知道哪些神经元之间相连,而且还引入了池化层,都导致了训练更加复杂。但本质思想上两者是一致的,都是误差逆传播。
一般卷积神经网络的结构为输入层->卷积层->采样层->卷积层->采样层->…->卷积层->采样层->输出层。比如如下图:

输出层
首先定义n个样本的代价函数
E=12∑Nn=1∑ci(zni−yni)2
则某个样本的误差为
Ed=12∑i(zi−yi)2
输出层的激活函数可以有很多种,这里用s函数,它的输出范围是0到1,通过训练让误差趋于0。所以更新公式为
wji←wji+ηδjxji
其中δj=−∂Ed∂nodej=δj=(tj−yj)yj(1−yj)。
采样层
netli,j为l层的加权输入,netl+1a,b则为l+1层的加权输入,于是可以得到
netl+1a,b=max(netli,j)
∂netl+1a,b∂netli,j为1,所以采样层只是将误差原封不动传递给上一层的卷积层。

如果使用了均值池化则是将误差平均分配到上一层卷积层对应的神经元上。
卷积层
现在只看步长为1、深度为1且filter为1的情况,左边绿色表示l-1层的输入,中间黄色是filter,右边红色是l层的误差项。

netl为l层神经元的加权输入数组,Wl为filter的权重数组,wb为filter偏置项,al−1为l-1层输出数组,设卷积操作为 conv,则有,
netl=conv(Wl,al−1)+wb
al−1i,j=fl−1(netl−1i,j)
l层的误差项可以通过上面的抽样层计算得到(可看成由输出层误差传递到抽样层),根据链式求导法则,有
δl−1i,j=∂Ed∂netl−1i,j=∂Ed∂al−1i,j∂al−1i,j∂netl−1i,j=∂Ed∂netli,j∂netli,j∂al−1i,j∂al−1i,j∂netl−1i,j
∂Ed∂netli,j则是对应l层的误差项;
∂netli,j∂al−1i,j,l-1层的输出相对于filter随着窗口的移动而会产生不同的误差分量,所以计算∂netli,j∂al−1i,j,相当于把第l层的误差项周围补一圈0,在与180度翻转后的filter进行互相关操作。

∂al−1i,j∂netl−1i,j则是激活函数的导数f′(netl−1i,j)。
所以,
δl−1i,j=∑m∑nwlm,nδli+m,j+nf′(netl−1i,j)























