课程设计——哈夫曼编码及解码
目录
- 一、课程设计的目的
- 二、设计需求分析
- 三、总体方案设计
- 四、各模块详细设计
- 六、设计结果分析
- 七、心得体会
一、课程设计的目的
当今信息技术高速发展,大量的信息会占用存储器的容量空间、通信信道的带宽,也给计算机的处理速度带来了极大的压力。要解决这个问题,我们不能单靠增加存储器容量、提高信道带宽以及计算机的处理速度等方法。这时就考虑到了信息压缩。压缩的关键在于编码,如果在对数据进行编码时,对于常见的数据,编码器输出较短的码字;而对于不常见的数据则用较长的码字表示,就能够实现压缩。压缩是一种实用性很强的方法,尤其在网络通讯中,它可以减小文件中的比特和字节总数,使文件能够通过较慢的互联网连接实现更快传输,此外它还可以减少文件的磁盘占用空间。在下载了文件后,计算机可使用WinRAR或7-zip这样的程序来展开文件,将其复原到原始大小,展开的文件与压缩前的原始文件将完全相同。
本课程设计使用哈夫曼编码方法实现对文本编码和解码,研究哈夫曼编码长度与权重之间的关系,使同学能更好地理解哈夫曼编码的原理及其特性,掌握压缩编码的基本过程。
二、设计需求分析
设计需求:
1.设计一个能统计输入字符出现次数的模块。
2.设计哈夫曼树,以字符集中各字符作为叶子结点,以出现次数为权值构造一棵哈夫曼树。
3.设计哈夫曼编码,按照构造出来的哈夫曼树,规定左分支为0,右分支为1,则从根到叶子结点的0和1 组成的序列便为该字符对应的哈夫曼编码。
4.设计哈夫曼解码器,能根据输入的哈夫曼编码进行解码。
设计原理:
哈夫曼编码是一种被广泛应用而且非常有效的数据压缩编码,它是可变长度编码。可变长编码即可以对待处理字符串中不同字符使用不等长的二进制位表示,可变长编码比固定长度编码好很多,可以对频率高的字符赋予短编码,而对频率较低的字符则赋予较长一些的编码,从而可以使平均编码长度减短,起到压缩数据的效果。
哈夫曼编码是前缀编码。如果没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。对前缀编码的解码也是相对简单的,因为没有一个码是另一个编码的前缀,所以可以识别出第一个编码,将它翻译为原码,再对余下的编码文件重复同样操作。
三、总体方案设计
本方案是通过层层子功能进行实现的,每个功能封装成一个子函数,通过主函数的控制完成整个功能的实现。
子模块一:初始化数组模块。它能对下一步需要用到的数组进行初始化。
子模块二:字符串接收与统计模块。它能接收输入的字符串,并统计每个字符出现的次数。
子模块三:哈夫曼树建立、存储与打印模块。它们能根据各个字符的权重建立一棵哈夫曼树,并打印哈夫曼树的顺序存储结构。
子模块四:哈夫曼编码与打印模块。它们能够根据已经建立的哈夫曼树生成各个字符的哈夫曼编码,并打印生成的哈夫曼编码。
子模块五:解码模块。它能够对输入的连续的哈夫曼编码进行解码。
四、各模块详细设计
原理介绍:
1.编码方式比较
哈夫曼编码是一种被广泛应用而且非常有效的数据压缩技术,根据待压缩数据的特征,一般可压缩掉20%~90%。这里考虑的数据指的是字符串序列。哈夫曼算法使用了一张字符出现频度表,根据它来构造一种将每个字符表示成二进制串的最优方式。
假设有一个包含100 000个字符的数据文件要压缩存储。各字符在该文件中的出现频度见下图:

可以用很多种方式来表示这样一个文件。我们来考虑设计一种二进制字符编码(或简称为编码)的问题,其中每一个字符都由唯一的二进制串来表示。如果采用固定长度编码,则需要三位二进制数字来表示六个字符:a=000, b=001,…,f=101,这种方法需要300 000位来对整个原文件编码,这是一种固定长度编码。
如果使用可变长编码进行编码,则比固定长度编码好得多,其特点是对频度高的字符赋以短编码,而对频度低的字符则赋以较长一些的编码。图1示出了这样一种编码,其中一位串0表示a,四位串1100表示f。这种编码方式需要
(45×1+13×3+12×3+16×3+9×4+5×4)×1000 = 224 000位
来表示整个文件,即可压缩掉约25%。实际上,对这个文件来说,这已是一种最优字符编码了。
2.哈夫曼编码过程
在给每个字符分配位模式前,首先根据每个字符的使用频率给它们分配相应的权值。在这个例子中,假定字符出现的频率如表1所示。字符A出现的频率为17%,字符B出现的频率为12%,等等。
表1 字符的出现频率
字符 | A | B | C | D | E |
频率 | 17% | 12% | 12% | 27% | 32% |
一旦建立了各个字符的权值后,就可以根据这些值构造一棵树。构造树的过程如图2所示。它遵循以下三个基本步骤:
1)将全部字符排成一排。每个字符现在都是树的最底层结点。
2)找出权值最小的两个结点并由它们合成第三个结点,产生一棵简单的二层树。新结点的权值由最初的两个结点的权值结合而成。这个结点,在叶子结点的上一层,可以再与其他的结点结合。请记住,选择所结合的两个结点的权值和必须比其他所有可能的选择小。
3)重复步骤2),直到各个层上的所有结点结合成为一棵树。

3.前缀编码及其解码
在哈夫曼编码中,没有一个编码是另一个编码的前缀,这样的编码称为前缀编码。
对任何一种二进制字符编码来说编码总是简单的,这只要将文件中表示每个字符的编码并置起来即可。例如,利用图1中的可变长度编码,把包含三个字符的文件abc编成0·101·100=0 101 100, 其中“·”表示并置。
在前缀编码中解码也是很方便的。因为没有一个码是其他码的前缀,故被编码文件的开始处的编码是确定的。我们只要识别出第一个编码,将它翻译成原文字符,再对余下的编码文件重复这个解码过程即可。在我们的例子中,可将串001 011 101唯一地分析为0·0·101·1101,因而可解码为aabe。
解码过程需要有一种关于前缀编码的方便表示,使得初始编码可以很容易地被识别出来。有一种表示方法就是叶子为给定字符的二叉树。在这种树中,我们将一个字符的编码解释为从根至该字符的路径,其中0表示“转向左子结点”,1表示“转向右子结点”。图3给出了与我们的例子中两种编码对应的二叉树。注意它们并不是二叉查找树,因为各叶结点无需以排序次序出现,且内结点也不包含关键字。

文件的一种最优编码总是由一棵满二叉树来表示的,树中每个非叶结点都有两个子结点。在例子中,固定长度编码不是最优编码,因为表示它的树(如图3a所示)不是满二叉树:有的编码开始于10…,但没有一个开始于11…。我们现在可以把注意力集中到满二叉树上,故可以说如果c是包含待编码字符的字母表且所有字符频度为正,则表示最优前缴编码的树中恰有|c|片叶子,每一片表示字母表中的一个字母,另还有|c|-1个内结点。
给定对应-种前缀编码的二叉树T,很容易计算出编码一个文件所需的位数。对字母表C中的每一个字符c,设!

表示c在文件中出现的频度,

表示c的叶子在树中的深度。注意

也是字符c的编码的长度。这样,编码一个文件所需的位数就是
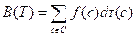
(式1)
我们把它定义为树T的代价。
变量解释:
本方案引用头文件’stdio.h’,用到其中’printf’,’scanf’等函数进行输入输出。定义宏’N’,’N’为本程序最多编码的字符数。本方案默认定义N=50,这样既可以满足大多数情况,又不会占用太多的空间。
由于本程序所声明的变量在程序运行期间多次用到,本方案多使用全局变量作为数据的载体。以下为所有全局变量的名称和含义:
min1:select()函数中所找到的满足要求的最小权重值。
min2:select()函数中所找到的满足要求的第二小权重值。
where1:min1所在的行(从1开始计数)。
where2:min2所在的行(从1开始计数)。
n:记录count_character_and_num()函数中统计的不同字符的个数。
str[100]:用来存储输入的字符串,最多为100个字符。
character_and_num_origin[127]:第零列存储0-127共128个字符的ASCII编码(由小到大),第一列存储各个字符对应的个数(权重)。
character_and_num[N]:第零列存储输入的字符的ASCII编码,第一列存储对应的个数(权重)。
huffman_matrix[2*N][6]:用来存储哈夫曼数组。
第零列:不使用;
第一列:权重;
第二列:父结点行号;
第三列:左孩子行号;
第四列:右孩子行号;
第五列:(布尔型)标记是否已经拥有父结点;
因为若要给n个字符编码,哈夫曼数组须有2n-1行,为了与课本一致,本方案不使用其第一行;
c[N][10]: 用来存储编码,因最多编码字符种数为N,所以定义c为N行;定义c为n列,表示本方案的编码最多不超过10位。
代码解释:
本方案共由8个函数构成,以下为所有函数的名称和含义:
1)start_character_and_num_origin()
功能:通过两个for循环使character_and_num_origin数组第零列为0-127共128个字符的ASCII编码(由小到大),第一列全为0。
初始化后为:
0 | 1 | 2 | 3 | .... |
0 | 0 | 0 | 0 | .... |
的转置数组。
流程图:
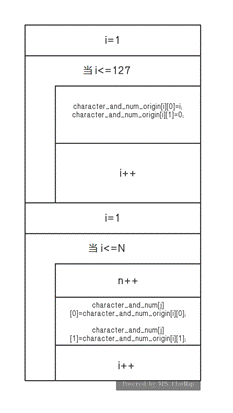
- string_input()
功能:将初始的字符串,存储至str数组中,并统计每个字符出现的次数。
局部变量:两个循环计数变量i,j;
实现方法:printf函数输出提示,scanf函数接纳字符串,对输入的字符逐个处理,若该字符ASCII编码为n,则character_and_num_origin数组的第n行第2列自增1。
流程图:
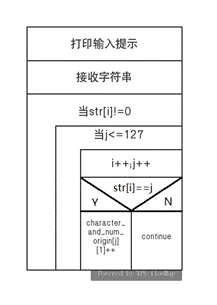
若输入ABBCD,则执行该函数后数组character_and_num_origin内容为:
.... | 65 | 66 | 67 | 68 | 69 | .... |
.... | 1 | 2 | 1 | 1 | 0 | .... |
的转置数组;
- count_character_and_num()
功能:将character_and_num_origin数组简化后存储为character_and _num数组,即将前者第二列不为0的行存储到后者的首部,后者的第零列存储输入的字符的ASCII编码,第一列存储对应的个数(权重);
流程图:
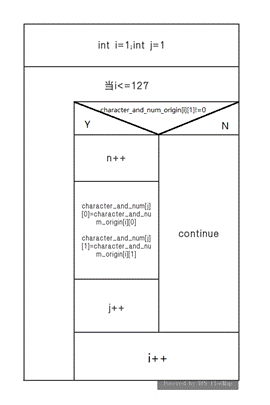
若输入ABBCD,则后者为:
65 | 66 | 67 | 68 | 0 | .... |
1 | 2 | 1 | 1 | 0 | .... |
的转置数组;
- initialize_mat_and_code()
功能:初始化huffman_matrix和c数组,使huffman_matrix所有元素为0;使c数组所有元素为2。
说明:由于若使c数组元素初始值全为0,则在输出以0为首编码时会分不清编码从哪里开始,因此全部赋初始值为2。
流程图:

初始化后,huffman_matrix数组为:
不使用 | 0 | 0 | 0 | 0 |
不使用 | 0 | 0 | 0 | 0 |
不使用 | 0 | 0 | 0 | 0 |
不使用 | 0 | 0 | 0 | 0 |
不使用 | 0 | 0 | 0 | 0 |
不使用 | 0 | 0 | 0 | 0 |
c数组为:
2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
…… | …… | …… | …… | …… | …… | …… | …… | …… | …… |
- creat_huffman_matrix()
功能:根据规则将权重生成哈夫曼数组。
实现方法:因count_character_and_num数组中的第一列是用来存储字符权重的,而_huffman_matrix数组的第一列也是用来存储权重的,因此第一步将count_character_and_num数组的第一列存储至_huffman_matrix数组的第一列,并用变量m标记当前还未存储权重的行中的第一行。第二步调用select()函数找到huffman_matrix中存储的两个最小的权值min1,min2和它们所在的位置where1,where2,并将第where1、where2行的第五列标记为1,即标记这个结点已经有父结点了。再将两个最小的权值加起来(min1+min2)赋值给第m行的第一列(建立新的结点),将where1和where2的值赋值给第m行的第三、四两列(记录新结点的左右子结点),最后再把m赋值给第where1、where2两行的第二列(记录两个权重最小结点的父结点)。由于一棵叶子结点为n的哈夫曼树总共有2*n-1个结点,因此循环该过程,建立一个个结点,直到m等于2*n完成哈夫曼树的建立。
流程图:

如输入字符为ABBCD,则huffman_matrix最终为:
data | Prnt | Lchild | Rchild | Sign |
1 | 5 | 0 | 0 | 1 |
2 | 6 | 0 | 0 | 1 |
1 | 5 | 0 | 0 | 1 |
1 | 6 | 0 | 0 | 1 |
2 | 7 | 1 | 3 | 1 |
3 | 7 | 4 | 2 | 1 |
5 | 0 | 5 | 6 | 0 |
哈夫曼树的建立过程是一个动态的过程,其中间过程如下:
data | Prnt | Lchild | Rchild | Sign |
1 | 0 | 0 | 0 | 0 |
2 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 | 0 |
data | Prnt | Lchild | Rchild | Sign |
1 | 5 | 0 | 0 | 1 |
2 | 0 | 0 | 0 | 0 |
1 | 5 | 0 | 0 | 1 |
1 | 0 | 0 | 0 | 0 |
2 | 0 | 1 | 3 | 0 |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 0 | 0 |
data | Prnt | Lchild | Rchild | Sign |
1 | 5 | 0 | 0 | 1 |
2 | 6 | 0 | 0 | 1 |
1 | 5 | 0 | 0 | 1 |
1 | 6 | 0 | 0 | 1 |
2 | 0 | 1 | 3 | 0 |
3 | 0 | 4 | 2 | 0 |
0 | 0 | 0 | 0 | 0 |
data | Prnt | Lchild | Rchild | Sign |
1 | 5 | 0 | 0 | 0 |
2 | 6 | 0 | 0 | 1 |
1 | 5 | 0 | 0 | 0 |
1 | 6 | 0 | 0 | 1 |
2 | 7 | 1 | 3 | 1 |
3 | 7 | 4 | 2 | 1 |
5 | 0 | 5 | 6 | 0 |
- print_huffman_matrix()
功能:打印哈夫曼数组。
实现方法:通过二重循环打印二维数组。
流程图:

- Coding()
功能:根据哈夫曼树对字符进行编码,并存储至c数组中(顺序为ASCII编码由小到大);
局部变量:当前编码列位置p;当前编码行位置row;循环计数变量i。
实现方法:哈夫曼树一共有2n-1个结点,程序只对前n个叶子结点进行哈夫曼编码,并从huffman_matrix的第一个叶子结点(即第一行)开始,依次开始编码。本模块通过两个循环进行控制,大循环每一个循环编一个字符的编码,循环条件是”i<=n”,即编完所有叶子结点就结束。小循环每一个循环编一个字符的一位,循环条件是”huffman_matrix[row][2]!=0”,即当前该结点没有父结点。
流程图:
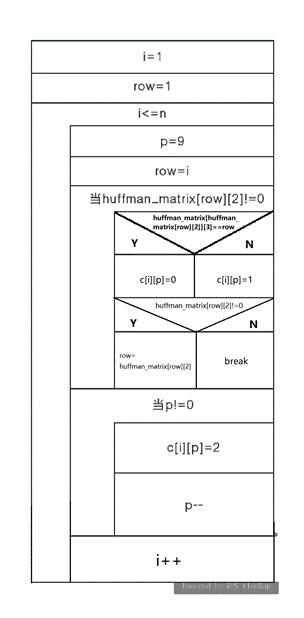
由于篇幅有限,仅列举给第一个字符A编码的详细过程,给字符A编码过程如下:
首先找到第一个结点第二列Prnt为5,
data | Prnt | Lchild | Rchild | Sign |
1 | 5 | 0 | 0 | 1 |
然后再看第五行的Lchild和Rchild,若Lchild为原行号”1”,说明第一个叶子结点在父结点的左子树上,则c数组末位赋值为0;若不为原行号”1”,则说明Rchild为”1”,c数组末位赋值为1。
data | Prnt | Lchild | Rchild | Sign |
2 | 7 | 1 | 3 | 1 |
根据实际情况,第五行的Lchild为原行号”1”,因此给c的末位赋值为0。再让标志变量p自减1,以便之后将编码的第二位存储至c的倒数第二位中。
再找到第五行的第二列Prnt为7,因此再看第七行的Lchild和Rchild。若Lchild为原行号”5”,说明第一个叶子结点在父结点的左子树上,则c数组末位赋值为0;若不为原行号”5”,则说明Rchild为”5”,因此c数组末位赋值为1。
data | Prnt | Lchild | Rchild | Sign |
5 | 0 | 5 | 6 | 0 |
根据实际情况,第七行的Lchild为原行号”5”,因此给c的倒数第二位赋值为0。再让标志变量p自减1。此时发现该行的Prnt的值为0,即它没有父结点,因此循环条件不满足,跳出循环。至此A的编码已经完成。
此时c数组中第一行为:
2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0 | 0 |
- print_code()
功能:打印编码。
局部变量:两个循环计数变量i,j。
实现方法:通过二重循环打印编码字符和对应哈夫曼编码。为了防止打印第一个字符为'0'的哈夫曼编码时分不清编码从哪里开始时有效位,所以编码时用'2'标记无效位,打印时遇到'2'打印一个空格。
流程图:

- recoding()
功能:解哈夫曼码。
局部变量:计数变量i,j,k,t、标记变量sign、拥有N(宏定义变量)行10列的二位字符型数组code、拥有100列的一维字符型数组code_order、拥有10列的一维字符型数组tem_code_order[10]。
实现方法:定义一个字符型的数组code,用二重循环将c数组中的哈夫曼编码存储至code数组中。再将待解码的哈夫曼编码存储至数组字符型数组code_order,将code_order的第一位复制至tem_code_order的第一位;将其与code的值循环比对,若比对成功输出该哈夫曼编码代表的意思,同时清空tem_code_order数组;若比对不成功则将code的第二位存储至tem_code_order的第二位,再比对,以此往复,直至需要复制至tem_code_order数组的那一位为’\0’,即解码完成。
说明:c数组中的哈夫曼编码是用整形变量存储的,code中的哈夫曼编码是用字符型变量存储的,这样之后,比较code数组与tem_code_order数组只需调用”string.h”头文件中的”strcmp”函数即可。
流程图:
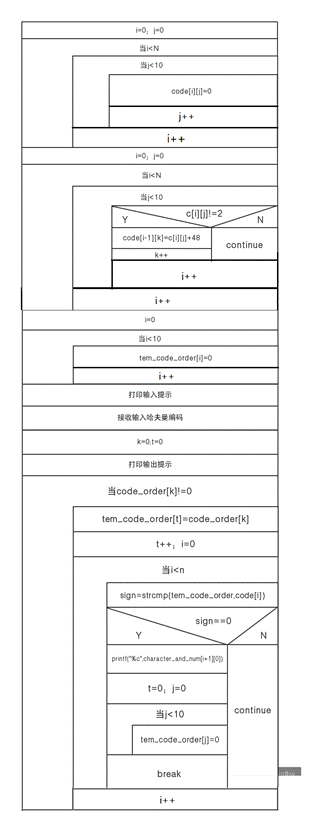
10)main主函数:依次执行以上各函数。
11)select()
功能:找到sign为0的两个最小权重结点,并将他们的权重赋值给min1,min2,将他们的行号赋值给where1,where2。
六、设计结果分析

在哈夫曼编码中,对于出现更为频繁的字符分配较短的编码,而对于次数出现较少的字符分配较长的编码。
下表为权重与码长的关系:
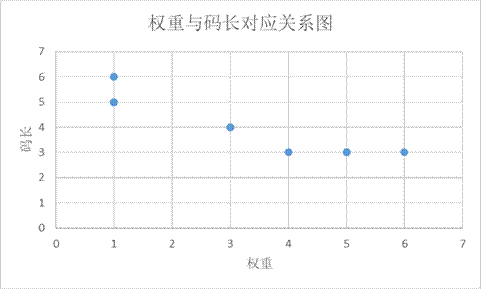
由此可见码长与权重近似成反相关。
下表为权重与码长的关系:
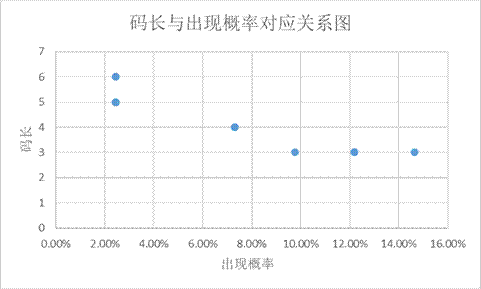
由此可见码长与出现概率近似成反相关。
有待改进之处:本方案只能对有ASCII编码的字符进行哈夫曼编码,对汉字等字符则不行。
七、心得体会
对于软件技术基础的课程设计,本人觉得是十分有好处的。从小学开始,本人对软件技术比较感兴趣,上学期的C语言课程学的也比较扎实,因此上手起来也较为容易。
这次课程设计完全是我自己写的,在我看来,完完整整地把哈夫曼树的建立、编码、解码等过程写出来是很有难度的,我也花了很长的时间,有几天弄到深夜。我将这看作是对我编程能力的一次考验,在编写程序、调试、修改中,我解决了一个又一个问题,也获得了成就感。本人觉得编程最重要的是兴趣,我在编程中感受到了成功的喜悦,因此能坚持到底,如果让我学习、从事文学领域的知识和工作,我可能就半途而废了。其次重要的是思路,原理懂了那么所有的问题都迎刃而解。本人最先想到的就是一个树的结构怎么来存储,在matlab中好像是容易一些,但是使用C语言就有点困扰了。经过较长的一段时间的思考,反复地调试,做成了现在这个样子,我按照哈夫曼树顺序存储的原理编写算法,编完代码再需要进行一定的封装再上交,实验报告也弄了很长时间,修改了很长的时间。本人觉得这个软件实验课程设计对动手和创新的能力是一个很好的锻炼,但是对于我一个非专业的学生来说还是有一定难度。不过顺利完成任务之后,感觉收获满满。这学期在汤老师的认真授课下,本人不仅对这个方向有了一定的了解,编程能力也得到了锻炼。
附 录(重要程序)
#include<stdio.h>
#include<string.h>
#define N 50
int huffman_matrix[2*N][6];
int min1,min2,where1,where2;
int c[N][10];
char str[100];
int character_and_num_origin[127][2];
int n=0;
int character_and_num[N][2];
void select(int m)//找到满足条件的两个最小权重结点,并将他们的权重赋值给min1,min2,将他们的行号赋值给where1,where2
{
int i;
min1=2147483647;
for(i=1;i<=m-1;i++)
{
if(huffman_matrix[i][1]<min1&&huffman_matrix[i][5]==0)
{
min1=huffman_matrix[i][1];
where1=i;
}
}
huffman_matrix[where1][5]=1;
min2=2147483647;
for(i=1;i<=m-1;i++)
{
if(huffman_matrix[i][1]<min2&&huffman_matrix[i][1]>=min1&&huffman_matrix[i][5]==0)
{
if(huffman_matrix[i][5]==0)
{
min2=huffman_matrix[i][1];
where2=i;
}
}
}
huffman_matrix[where2][5]=1;
}
void initialize_mat_and_code()//初始化huffman_matrix和c数组,使其所有元素为0
{
int i,j;
for(i=1;i<=2*N-1;i++)
{
for(j=1;j<=5;j++)
{
huffman_matrix[i][j]=0;
}
}
for(i=1;i<=N;i++)
{
for(j=0;j<10;j++)
{
c[i][j]=0;
}
}
}
void creat_huffman_matrix()//根据规则将权重生成哈夫曼数组
{
int i,m;
for(i=1;i<=n;i++)
{
huffman_matrix[i][1]=character_and_num[i][1];
}
m=n+1;
while(m!=2*n)
{
select(m);
huffman_matrix[m][1]=min1+min2;
huffman_matrix[m][3]=where1;
huffman_matrix[m][4]=where2;
huffman_matrix[where1][2]=m;
huffman_matrix[where2][2]=m;
m++;
}
}
void print_huffman_matrix()//打印哈夫曼数组
{
int i,j;
printf("row\tdata\tPrnt\tLchild\tRchild\n");
for(i=1;i<=2*n-1;i++)
{
printf("%d\t",i);
for(j=1;j<=4;j++)
{
printf("%d\t",huffman_matrix[i][j]);
}
printf("\n");
}
}
void coding()//根据哈夫曼树对字符进行编码,并存储至c数组中
{
int p,row=1,i;
for(i=1;i<=n;i++)
{
p=9;
row=i;
while(huffman_matrix[row][2]!=0)
{
if(huffman_matrix[huffman_matrix[row][2]][3]==row)
c[i][p]=0;
else
c[i][p]=1;
if(huffman_matrix[row][2]!=0)
row=huffman_matrix[row][2];
else
break;
p--;
}
while(p!=0)
{
c[i][p]=2;
p--;
}
}
}
void print_code()//打印编码
{
int i,j,k=1;
printf("\n");
for(i=1;i<=n;i++)
{
printf("'%c'的编码为:",character_and_num[i][0]);
for(j=1;j<10;j++)
{
if(c[i][j]==2)
{
printf(" ");
}
else
{
printf("%d",c[i][j]);
}
}
printf("\n");
k++;
}
}
void string_input()//将初始的字符串,存储至str数组中,并统计每个字符出现的次数
{
int i,j;
printf("请输入字符串:\n");
scanf("%[^\n]",&str);
for(i=0;str[i]!=0;i++)
{
for(j=0;j<=127;j++)
{
if(str[i]==j)
{
character_and_num_origin[j][1]++;
}
}
}
}
void start_character_and_num_origin()//初始化character_and_num_origin数组
{
int i;
for(i=1;i<=127;i++)
{
character_and_num_origin[i][0]=i;
character_and_num_origin[i][1]=0;
}
for(i=1;i<N;i++)
{
character_and_num[i][0]=0;
character_and_num[i][1]=0;
}
}
void count_character_and_num()//将character_and_num_origin数组简化后存储为character_and _num数组,即将前者第二列不为0的行存储到后者的首部
{
int i,j=1;
for(i=1;i<=127;i++)
{
if(character_and_num_origin[i][1]!=0)
{
n++;
character_and_num[j][0]=character_and_num_origin[i][0];
character_and_num[j][1]=character_and_num_origin[i][1];
j++;
}
}
}
void recoding()//解码
{
int i,j,k,t,sign;
char code[N][10];
char code_order[100];
char tem_code_order[10];
for(i=0;i<N;i++)
{
for(j=0;j<10;j++)
{
code[i][j]=0;
}
}
for(i=1;i<=n;i++)
{
k=0;
for(j=1;j<10;j++)
{
if(c[i][j]!=2)
{
code[i-1][k]=c[i][j]+48;
k++;
}
}
}
for(i=0;i<10;i++)
{
tem_code_order[i]=0;
}
printf("请输入需要解码的哈夫曼编码序列:\n");
scanf("%s",&code_order);
k=0;
t=0;
printf("解出来为:\n");
while(code_order[k]!=0)
{
tem_code_order[t]=code_order[k];
t++;
for(i=0;i<n;i++)
{
sign=strcmp(tem_code_order,code[i]);
if(sign==0)
{
printf("%c",character_and_num[i+1][0]);
t=0;
for(j=0;j<10;j++)
{
tem_code_order[j]=0;
}
break;
}
}
k++;
}
if(tem_code_order[0]!=0)
{
printf("\n警告!请检查输入编码!以上结果不一定准确!");
}
printf("\n");
}
void main()
{
start_character_and_num_origin();
string_input();
count_character_and_num();
initialize_mat_and_code();
creat_huffman_matrix();
print_huffman_matrix();
coding();
print_code();
recoding();
}参考文献
[1] 华继钊,汤正兰,李志军,夏晓楠. 软件技术基础. 杭州:浙江大学出版社,2013
[2] 谭浩强. C程序设计. 北京:清华大学出版社,1991
[3](美)佛罗赞,(美)莫沙拉夫. 计算机科学导论. 北京:机械工业出版社,2009
[4](美)Stephen Prata. C++ Prime Plus. 北京:人民邮电出版社,2005
[5] 周彩英. C语言程序设计教程. 北京:清华大学出版社,2011
[6](美)Thomas H. Cormen. 算法导论. 北京:机械工业出版社,2006























