多变量cox回归可视化

这节的主要内容来啦：
1. 多元变量引入
2. 梯度下降算法在多元变量的情况下的实现
3. 梯度下降算法的实际应用：特征缩放
4. 梯度下降算法的实际应用：学习率α

1、多元变量

之前我们都是只有一个对应的输入x和对应输出y的线性回归问题，这一节我们将要学习多变量的（即存在x1,x2,x3…）的线性回归问题。如图是预测房价模型的多变量表示：

因此我们可以将预测函数h表示成下面的形式：

同样根据我们之前学习的矩阵，我们也可以将x和θ看作一个一维向量，从而预测函数h就可以看作x向量和θ向量的转置相乘的结果。

2、多元变量的梯度下降算法

首先我们给出多元变量下的代价函数J的表达方式：

然后根据代价函数可以求得多元变量情况下的梯度下降算法的表达式，这里用到了微积分多元变量求导的方法，在高等数学中有详细的介绍。如图为梯度下降算法：

3、特征缩放

使用特征缩放的目的是可能有些特征值x取值范围差别很大，造成梯度下降的速度很慢，通过缩放使得每个特征值都处于相似（差别不大）的范围内，因此梯度下降的速度较快。

举例，例如特征值x1，x2的取值范围分别是[0,2000]和[1,5]，那么他们的差别很大，通过特征缩放，使得x1，x2的范围相同：

更一般的形式：

其中μ1表示平均值，s1表示范围（最大值 - 最小值）

4、学习率

通常用J（θ）关于迭代次数的函数来表示梯度下降算法的进行程度。

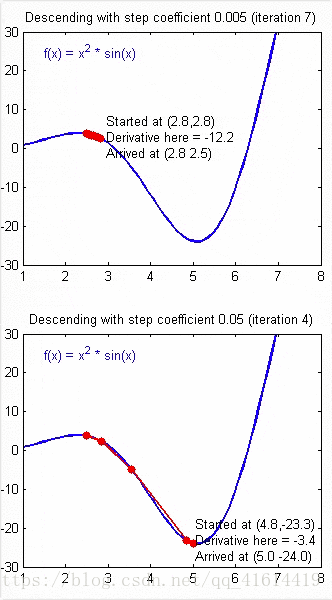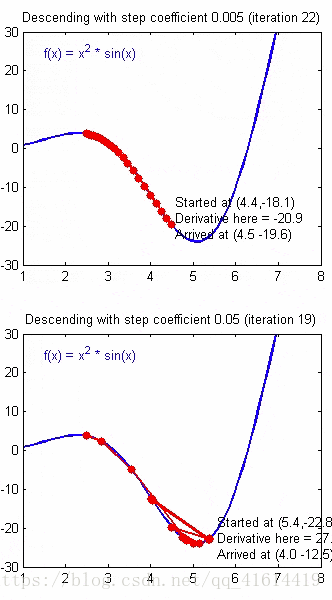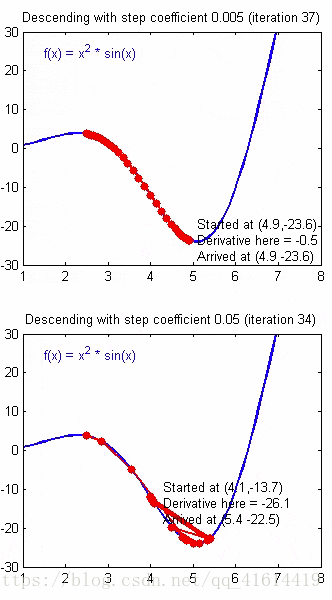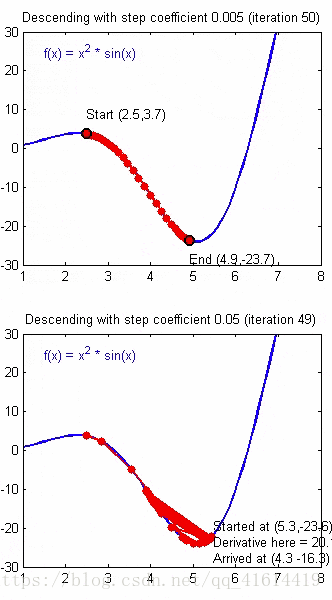
接下来讨论关于学习效率α对于代价函数的影响，α需要取一个合适的值才能保证梯度下降算法的有效性。如果太大会不断越过局部最小值；而如果太小，则算法效率很低，需要迭代很多次才能达到较好的训练结果。如下图说明了α过大和过小对于收敛的影响：

5、正规方程