Eden寒假日更_04——损失函数与优化_02
- softmax损失
- 优化
- 每日面试(葫芦书)
softmax损失
除了多类别SVM损失函数之外,深度学习中另外的一个流行选择是多项逻辑斯蒂回归,现如今它通常将
softmax函数作为他的损失函数。这个损失函数在深度学习领域可能使用得更为广泛。
回顾之前提到的SVM损失函数,我们并没有对通过函数后的得分做过多的解释,我们知识希望正确分类的得分比不正确分类的得分要高才好,但是在逻辑斯蒂回归的损失函数中,我们将赋予得分一些额外的含义,而且这些分数还会用来针对我们的类别,去计算概率分布。通过softmax函数后,每个变量针对不同类别的得分将被归一化,所有得分将分布在0-1之间,这就代表着归为某类的概率,且所有得分之和恒为1。
这里直接贴出一张给猫做三分类的softmax损失值计算过程:

通过softmax的计算公式可知,其最大值为正无穷,其最小值为0。一般监督学习的方法已经差不多梳理完了,这里贴出一张总结图:

优化
cs231n中对块儿介绍较少,这里只给出几个概念:
梯度:损失函数对w或b进行求导的偏导数列向量。
优化目的:使损失函数不断下降,最终找到合适的w和b。
优化手段:梯度下降,使损失函数的值延负梯度方向不断减小,同时w和b及其梯度也将实时更新。
这些概念非常基础,但是也是深度学习的核心,需要在不断的实践与练习中加深体会,这里就不过多展开了。
每日面试(葫芦书)
CH01卷积基础知识与变种
Q1:简述卷积层操作,并说出它与全连接层相比较最突出的几个特征。
A1:简单来说,卷积层是通过特定数目的卷积核(滤波器)对输入的多通道特征图进行扫描和运算,从而得到多个拥有更高层语义信息的输出特征图。扫描方式由认为自设卷积核尺寸和移动步长决定,运算方式为相乘相加。
其最突出的特征如下:
- 局部链接:
卷积核尺寸一般小于输入特征图的尺寸,这就意味着输出层上的节点都只与输入层的部分节点连接,这里存在一个感受野的概念。与之不同的是,全连接层之间,节点的连接时稠密的,输出层中所有节点与输入层中所有节点都存在关联。 - 参数共享:
由于卷积核窗口滑动机制,输出层中的节点与输入层中的连接权值完全相同(因为共用一个卷积核),在全连接层之间,不同节点的连接权重都是不一样的。 - 结构化输入输出:
如果将二维图片或者三维视频(多个连续帧二维图片)作为卷积层的输入,那么输出层特征图中的不同节点仍然会保留和原图基本一致的空间、时间信息。若是将这种结构化信息输入全连接层,其输出数据将会被拉伸为一维数组,在一定程度上来说,它并不具备空间乃至时间的分布特点。
Q2在卷积神经网络中,如何计算各层的感受野大小?
A2:假定卷积核尺寸为axa,移动步长为b,第i层卷积层输输出尺寸为cxc,则第(i-1)层中感受野尺寸为:(c+2b)x(c+2b),再往前一层推的时候,把卷积核相关的数据带进去就行,这个太简单就不做推导了,画画图就明白了。
Q3:卷积层的输出尺寸、参数量和计算量。
A3:
- 输出尺寸
个人认为,卷积层输出尺寸的计算和前置层感受野大小的计算互逆,所以没必要给出例子来说明了。 - 参数量
总参数量=输入层通道数 * 输出层特征图数 * 卷积核参数量(尺寸决定) - 计算量
计算量由滑动次数和参数量决定,所以计算量=总参数量 * 输出层特征图尺寸
Q4:请简述分组卷积、转置卷积、空洞卷积、可变形卷积工作原理及其适用场景。
A4:
- 分组卷积:
普通卷积中,输入层通道数和卷积核通道数相等,所以一个输出特征图中包含了原输入层每个通道的信息(相乘累加,在通道这个维度上等于全连接),分组卷积则不然,每个卷积核只保留设定的层数,用于提取特定层数的信息,这样做可以有效减小总体计算量,多被用来构建用于移动设备的小型网络模型,例如深度可分离卷积,但是其减少计算量却不能减少对内存的访问频繁程度,所以效果也没那么好。
这里贴出一张普通卷积和分组卷积的对比图

- 转置卷积:
转置卷积又称反卷积,,它可以看作是普通卷积的一个对称操作,我们可以把卷积看作是一种矩阵相乘的运算,设原卷积过程为:Y1(输出特征)=W(卷积核)X(输入特征),那么反卷积的过程就是:Y2(输出特征)=W转置(反卷积的卷积核)*Y1(输入特征)。值得注意的是,反卷积并不能恢复所有的数据,只能恢复原特征图的尺寸,它主要用于对特征图进行扩张或者上采样,所以一般还会配合各种插值方法进行工作,在语义分割、实例分割,自编码器等场景下有着广泛的运用。 - 空洞卷积:
空洞卷积,顾名思义,就是在卷积核内部数据点之间进行挖空操作,这样能增加卷积核的感受野,同时不用进行下采样等降低信息的操作。这里贴出两张经典动图对比一下普通卷积和空洞卷积。
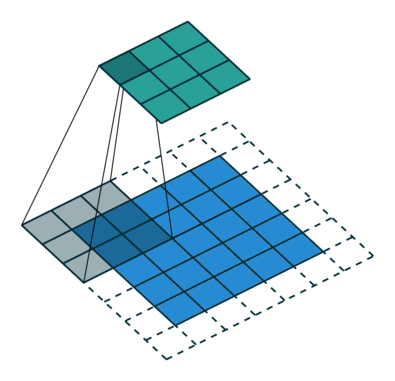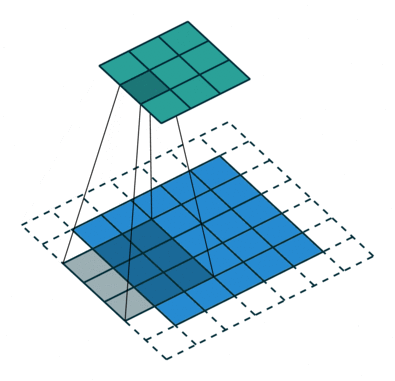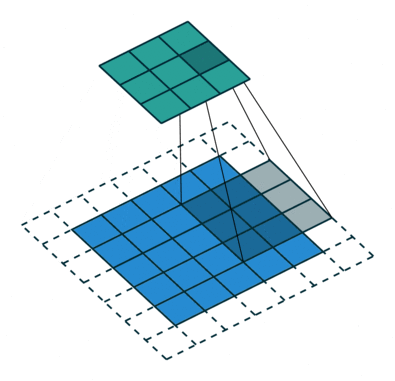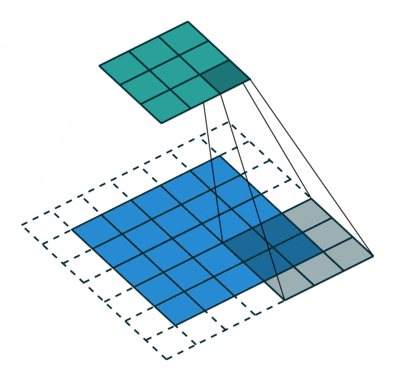
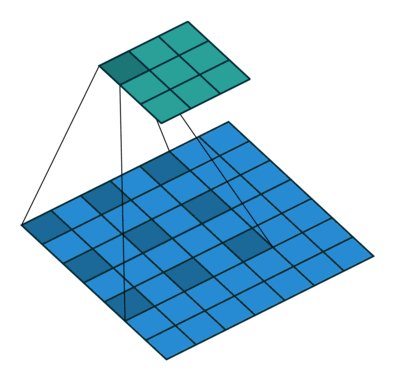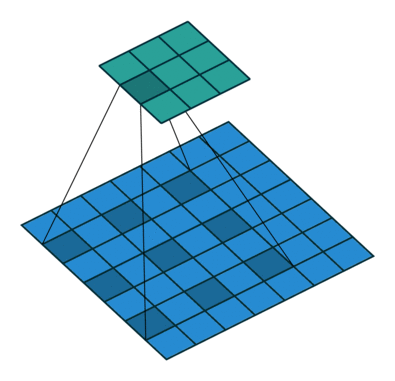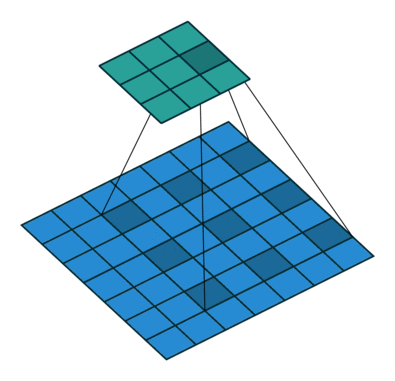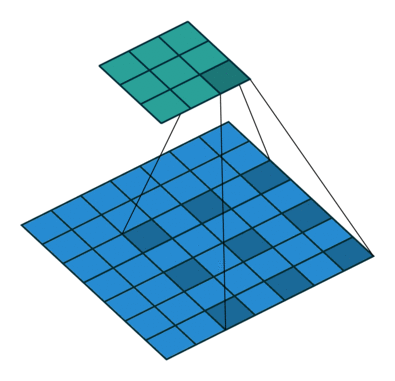
由此对比可以看出,空洞卷积利用了空洞结构扩大了卷积核尺寸, 不经过下采样操作即可增大感受野,同时还能保留输入数据的内部结构,通常被用于语义分割等任务的特征提取环节。
- 可变形卷积:
普通的卷积操作是在固定的、规则的网格点上进行数据采样,这就对网络的感受野形状产生了束缚,限制了网络对于几何形变的适应能力,为了克服这样的缺点,可变性卷积应运而生,他在卷积核的每个采样点上添加了一个可学习的偏移量(offset),让采样点不再局限于规则的网格点,值得一提的是,上面介绍的空洞卷积也是可变形卷积的一种特殊形式,这里贴出一张可变形卷积的示意图。
适应物体在不同图片或图片不同位置的复杂几何形变(如尺度变化、形态变化、刚性形变等),一直都是物体检测与识别领域一个难点,可变形卷积可以端到端的学习几何形变的偏移量,不需要额外的监督信息,并且知识增加了少许的计算量,最终却能显著提升同一物体的识别效果。
如上图可以看到,可变形卷积的采样点数量不变,但可以通过学习偏移量offset,实现针对物体形变的自适应调整,采样点针对同一物体的不同形态,能够呈现不同的分布(密度、位置),这样大大提升了物体检测与识别的灵活性与准确性。























