Force-Directed Algorithm 力导引算法
1 介绍
力导向算法是一个图布局的算法。一般来说,力导向算法包含一下步骤:对网络型数据进行力学建模,通过一定的时间模拟,得到一个稳定的布局。
对适用于一般网状结构数据绘图的算法来说,力导向算法是一种常被应用的方法。通过对每个节点的计算,算出引力和排斥力综合的合力,再由此合力来移动节点的位置。执行一次后根据节点新位置算出新的能量值,如同力学概念,能量值越小,表示整个网络越趋于稳定。一般来说能量值越小,网络图的配置显示就会越清晰,因此当能量值到达最小值的时候,网状图的配置状态就是我们想要的结果。
这种方法的缺点是不收敛,总是有节点在两个不同位置上来回振动,虽然不会收敛,但是来回振动时的配置通常也最终可达到某种稳定的状态,因此实际的执行都以指定执行的次数来决定停止的条件。另外一个问题就是网状图的节点数太多时,也无法求得令人满意的结果。
当开始配置不好的情况下,通常是力导向算法的配置结果也不是很好,所以使用力导向算法通常会配合一个初始配置的算法,以达成较满意的网状配置。
多级算法(multilevel algorithm)最重要的是代表节点的选择,这样就会直接影响到执行效率和结果。
2 代码实现以及效果
2.1 选择的语言以及技术方案
选择的为C#作为开发语言,展示方案使用WPF绘制展示
2.2 借鉴资料
- 《图布局力导引算法研究与实现》
- 《3 Force-directed Graph Drawing Algorithm》
2.3 实现方法以及关键代码
- 随机生成点以及关系,绘制
- 迭代循环对点进行调整
- 点与点之间产生斥力,推动点与点的分散
- 关系之间的点产生引力,拉近点与点的距离
- 上述两个产生的合力,使点的位置发生变化
2.3.1 随机创建点以及关系
Random random = new Random();
int radius = 40;
List<ShapeCircle> ListRoundedCircle = null;
List<ShapeRelationshipLine> ListShapeRelationshipLine = null;
CollisionGenerator pCollisionGenerator = null;
private void btnCreateRelNode_Click(object sender, RoutedEventArgs e)
{
int GraphWidth = Convert.ToInt32(this.stackPanelFather.ActualWidth)- radius;
int GraphHeight= Convert.ToInt32(this.stackPanelFather.ActualHeight) - radius;
int NodeCount = Convert.ToInt32(tbNodeCount.Text);
int RelCount= Convert.ToInt32(tbRelCount.Text);
bool IsShowRelNode = cbShowRelNode.IsChecked == true;
ListRoundedCircle = new List<ShapeCircle>();
for (int i = 0; i < NodeCount; i++)
{
int startX = random.Next(radius, GraphWidth);
int startY = random.Next(radius, GraphHeight);
ShapeCircle roundedCircle = new ShapeCircle()
{
DisplayName =string.Format("测试{0}",i),
CenterX = startX,
CenterY = startY,
Width = 2 * radius,
Height=2* radius
};
ListRoundedCircle.Add(roundedCircle);
}
Dictionary<string, Tuple<int,int>> dicHas = new Dictionary<string, Tuple<int, int>>();
for (int i = 0; i < RelCount; i++)
{
int StartNodeIndex = random.Next(0, ListRoundedCircle.Count);
int EndNodeIndex = random.Next(0, ListRoundedCircle.Count);
if (StartNodeIndex == EndNodeIndex)
{
continue;
}
if (StartNodeIndex > EndNodeIndex)
{
int TempIndex = EndNodeIndex;
EndNodeIndex = StartNodeIndex;
StartNodeIndex = TempIndex;
}
string strKey = $"{StartNodeIndex},{EndNodeIndex}";
if (dicHas.ContainsKey(strKey))
{
continue;
}
else
{
dicHas.Add(strKey,new Tuple<int, int>(StartNodeIndex, EndNodeIndex));
}
}
ListShapeRelationshipLine = new List<ShapeRelationshipLine>();
foreach (var item in dicHas)
{
int StartNodeIndex = item.Value.Item1;
int EndNodeIndex = item.Value.Item2;
ShapeCircle StartShapeCircle = ListRoundedCircle[StartNodeIndex];
ShapeCircle EndShapeCircle = ListRoundedCircle[EndNodeIndex];
ShapeRelationshipLine pShapeRelationshipLine = new ShapeRelationshipLine()
{
StartShapeCircle = StartShapeCircle,
EndShapeCircle = EndShapeCircle
};
ListShapeRelationshipLine.Add(pShapeRelationshipLine);
}
if (IsShowRelNode)
{
List<ShapeCircle> listRemoveNode = new List<ShapeCircle>();
listRemoveNode.AddRange(ListRoundedCircle);
foreach (var item in dicHas)
{
int StartNodeIndex = item.Value.Item1;
int EndNodeIndex = item.Value.Item2;
ShapeCircle StartShapeCircle = ListRoundedCircle[StartNodeIndex];
if (listRemoveNode.Contains(StartShapeCircle))
{
listRemoveNode.Remove(StartShapeCircle);
}
ShapeCircle EndShapeCircle = ListRoundedCircle[EndNodeIndex];
if (listRemoveNode.Contains(EndShapeCircle))
{
listRemoveNode.Remove(EndShapeCircle);
}
}
foreach (var item in listRemoveNode)
{
ListRoundedCircle.Remove(item);
}
}
ucGraphCanvas.IninGraphRelNode(ListShapeRelationshipLine,ListRoundedCircle);
}2.3.2 迭代循环对点进行调整
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace GraphAlgorithm
{
public class GraphForceDirectedAlgorithm
{
double CANVAS_WIDTH = 200;
double CANVAS_HEIGHT = 200;
private List<ShapeCircle> mNodeList;
private List<ShapeRelationshipLine> mEdgeList;
private Dictionary<ShapeCircle, double> mDxMap = new Dictionary<ShapeCircle, double>();
private Dictionary<ShapeCircle, double> mDyMap = new Dictionary<ShapeCircle, double>();
private Dictionary<ShapeCircle, ShapeCircle> mNodeMap = new Dictionary<ShapeCircle, ShapeCircle>();
private double k;
public GraphForceDirectedAlgorithm(List<ShapeCircle> nodeList, List<ShapeRelationshipLine> edgeList,double canvas_width,double canvas_height)
{
this.mNodeList = nodeList;
this.mEdgeList = edgeList;
this.CANVAS_WIDTH = canvas_width;
this.CANVAS_HEIGHT = canvas_height;
if (nodeList != null && nodeList.Count != 0)
{
k = Math.Sqrt(CANVAS_WIDTH * CANVAS_HEIGHT / (double)mNodeList.Count);
}
if (nodeList != null)
{
for (int i = 0; i < nodeList.Count; i++)
{
ShapeCircle node = nodeList[i];
if (node != null)
{
mNodeMap.Add(node, node);
}
}
}
}
public void Collide()
{
CalculateRepulsive();
CalculateTraction();
UpdateCoordinates();
}
/**
* 计算两个Node的斥力产生的单位位移。
* Calculate the displacement generated by the repulsive force between two nodes.*
*/
private void CalculateRepulsive()
{
double distX, distY, dist;
for (int v = 0; v < mNodeList.Count; v++)
{
ShapeCircle pStartShapeCircle = mNodeList[v];
mDxMap.Put(pStartShapeCircle, 0.0);
mDyMap.Put(pStartShapeCircle, 0.0);
for (int u = 0; u < mNodeList.Count; u++)
{
if (u != v)
{
ShapeCircle pEndShapeCircle = mNodeList[u];
distX = pStartShapeCircle.CenterX - pEndShapeCircle.CenterX;
distY = pStartShapeCircle.CenterY - pEndShapeCircle.CenterY;
dist = Math.Sqrt(distX * distX + distY * distY);
if (dist >= 0 && dist <= 200)
{
mDxMap.Put(pStartShapeCircle, mDxMap[pStartShapeCircle] + (distX / dist * k * k / dist ));
mDyMap.Put(pStartShapeCircle, mDyMap[pStartShapeCircle] + (distY / dist * k * k / dist ));
}
}
}
}
}
/**
* 计算Edge的引力对两端Node产生的引力。
* Calculate the traction force generated by the edge acted on the two nodes of its two ends.
*/
private void CalculateTraction()
{
int condenseFactor = 3;
ShapeCircle startNode, endNode;
for (int e = 0; e < mEdgeList.Count; e++)
{
ShapeCircle eStartID = mEdgeList[e].StartShapeCircle;
ShapeCircle eEndID = mEdgeList[e].EndShapeCircle;
startNode = mNodeMap[eStartID];
endNode = mNodeMap[eEndID];
if (startNode == null)
{
Console.WriteLine("Cannot find node id: " + eStartID + ", please check it out.");
return;
}
if (endNode == null)
{
Console.WriteLine("Cannot find node id: " + eEndID + ", please check it out.");
return;
}
double distX, distY, dist;
distX = startNode.CenterX - endNode.CenterX;
distY = startNode.CenterY - endNode.CenterY;
dist = Math.Sqrt(distX * distX + distY * distY);
mDxMap.Put(eStartID, mDxMap[eStartID] - (distX * dist * dist / k));
mDyMap.Put(eStartID, mDyMap[eStartID] - (distY * dist * dist / k));
mDxMap.Put(eEndID, mDxMap[eEndID] + (distX * dist * dist / k));
mDyMap.Put(eEndID, mDyMap[eEndID] + (distY * dist * dist / k));
}
}
/**
* 更新坐标。
* update the coordinates.
*/
private void UpdateCoordinates()
{
int maxt = 4, maxty = 3; //Additional coefficients.
for (int v = 0; v < mNodeList.Count; v++)
{
ShapeCircle node = mNodeList[v];
int dx = (int)Math.Floor(mDxMap[node]);
int dy = (int)Math.Floor(mDyMap[node]);
if (dx < -maxt) dx = -maxt;
if (dx > maxt) dx = maxt;
if (dy < -maxty) dy = -maxty;
if (dy > maxty) dy = maxty;
double PointCenterX = Math.Min(node.CenterX, CANVAS_WIDTH);
double PointCenterY = Math.Min(node.CenterY, CANVAS_HEIGHT);
PointCenterX = Math.Max(PointCenterX, 0);
PointCenterY = Math.Max(PointCenterY, 0);
node.CenterX = ((PointCenterX + dx) >= CANVAS_WIDTH || (PointCenterX + dx) <= 0 ? PointCenterX - dx : PointCenterX + dx);
node.CenterY = ((PointCenterY + dy) >= CANVAS_HEIGHT || (PointCenterY + dy <= 0) ? PointCenterY - dy : PointCenterY + dy);
}
}
List<ShapeCircle> getNodeList()
{
return mNodeList == null ? new List<ShapeCircle>() : mNodeList;
}
}
}2.4 效果图
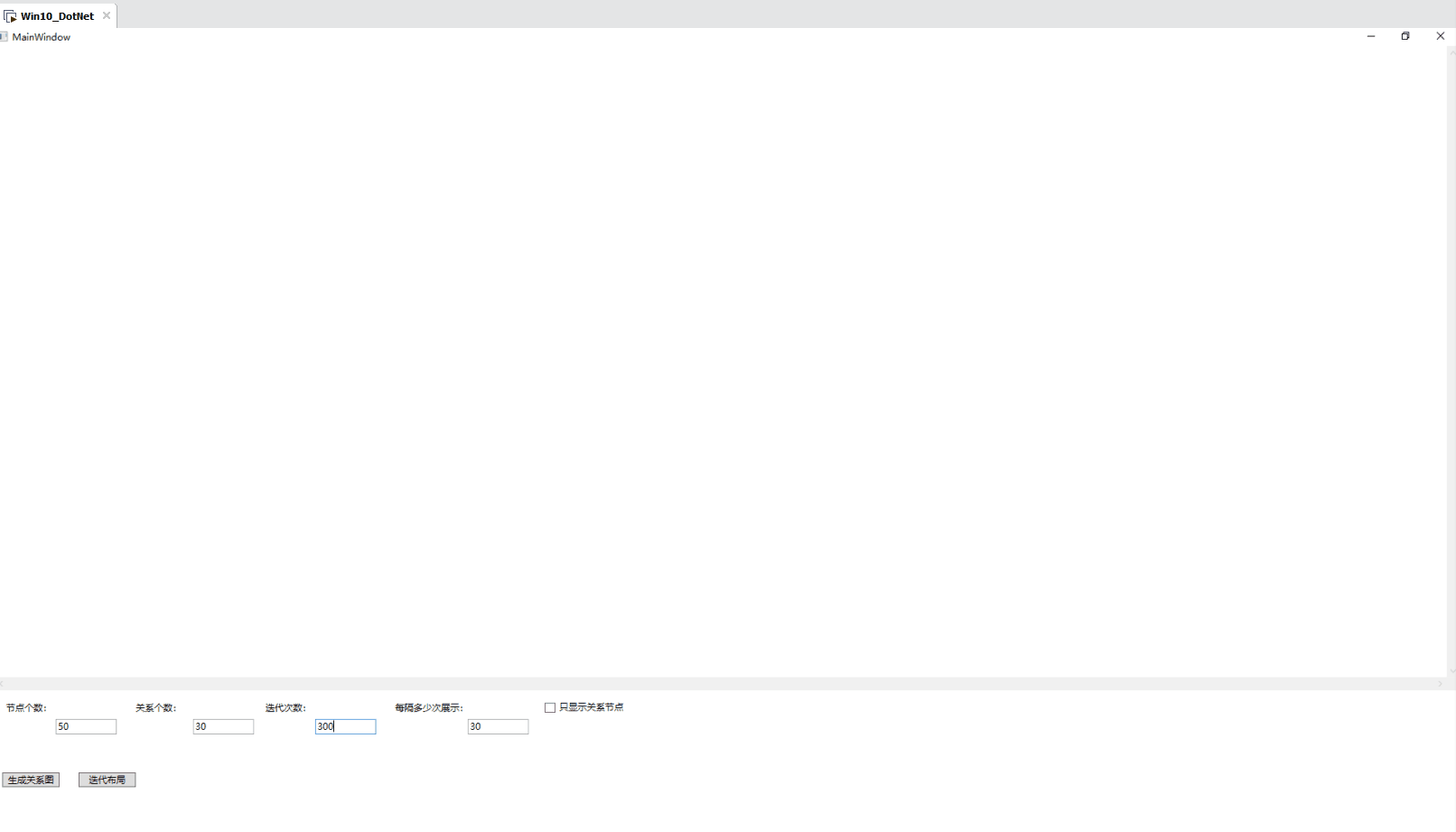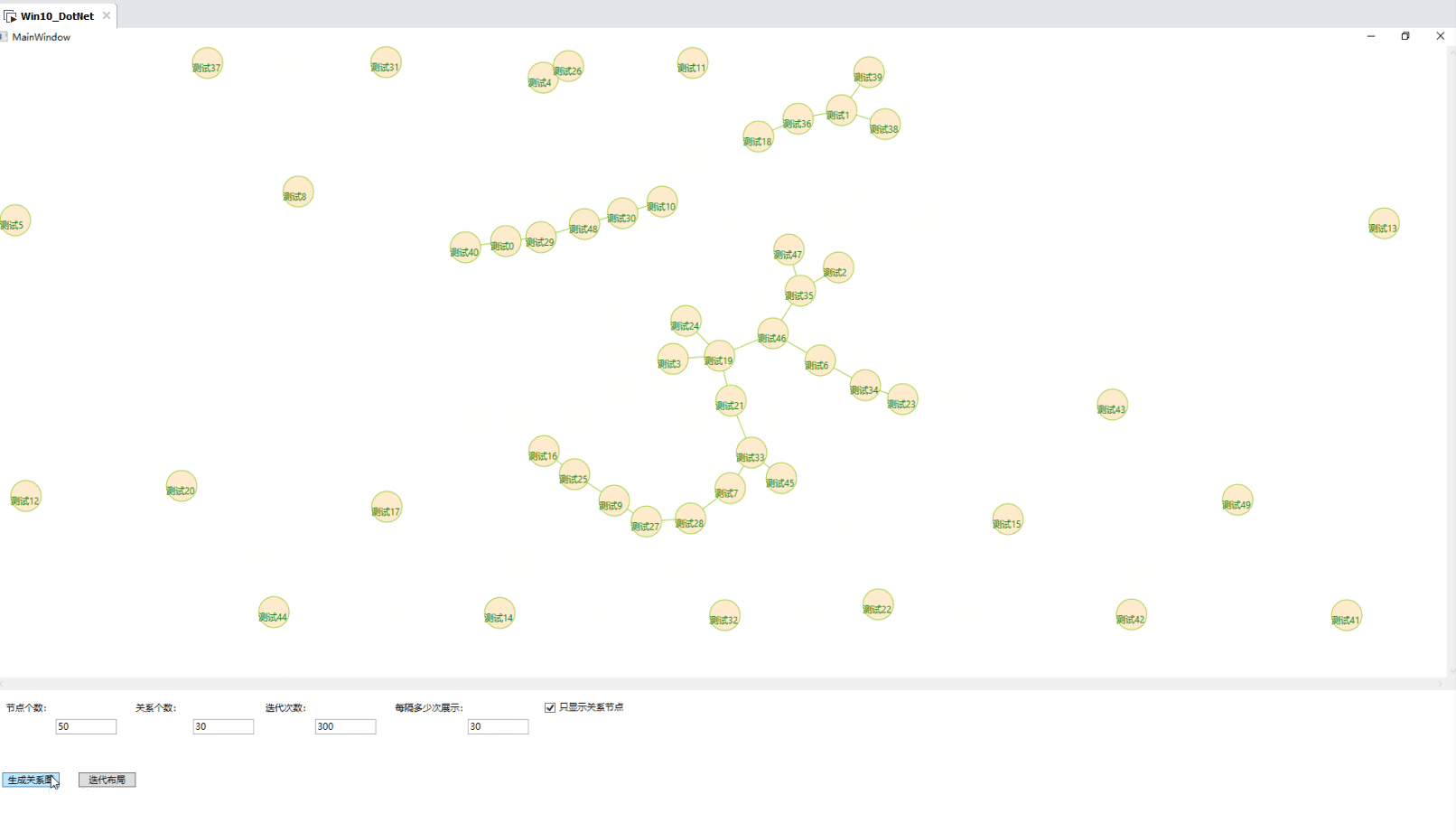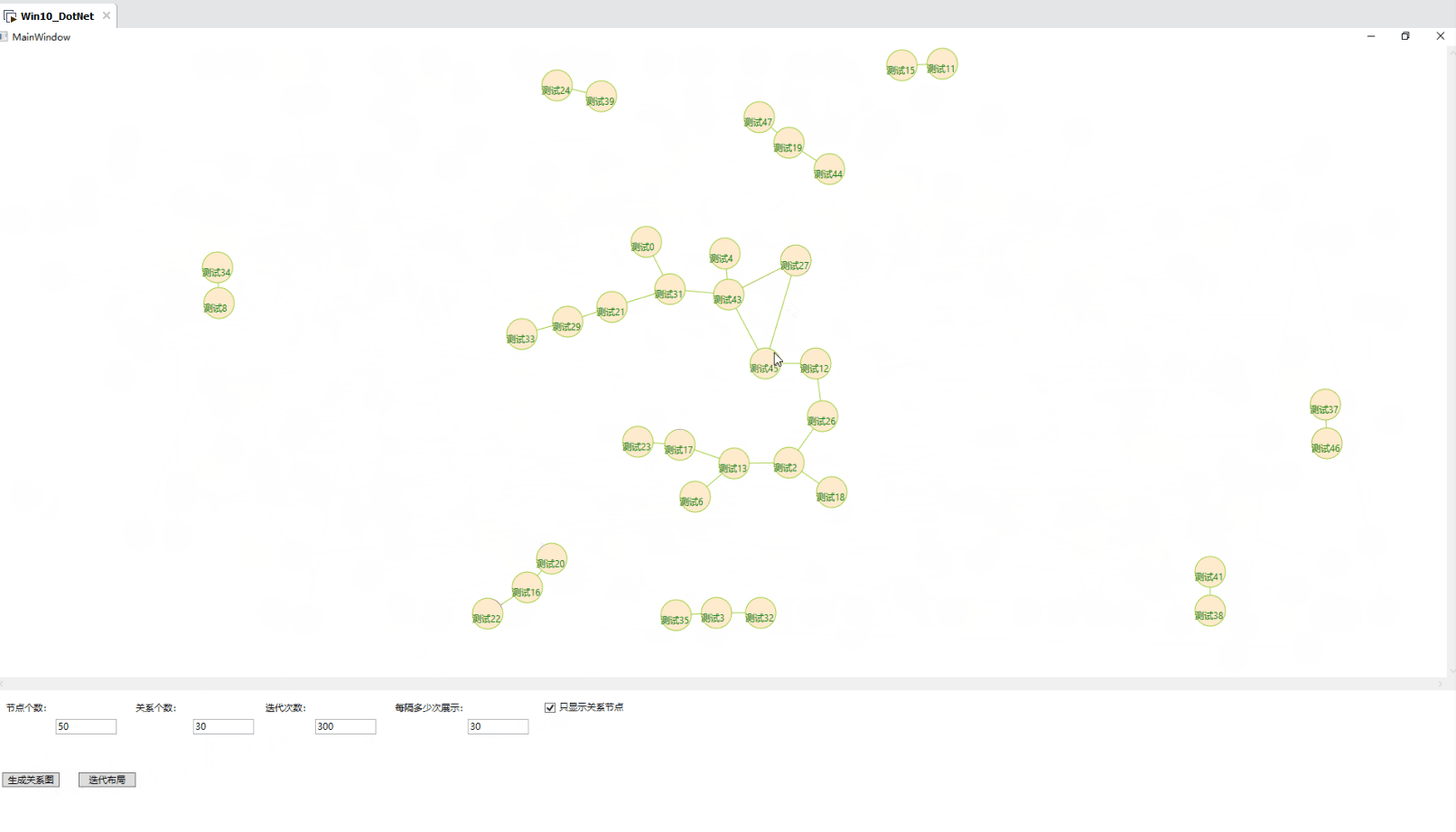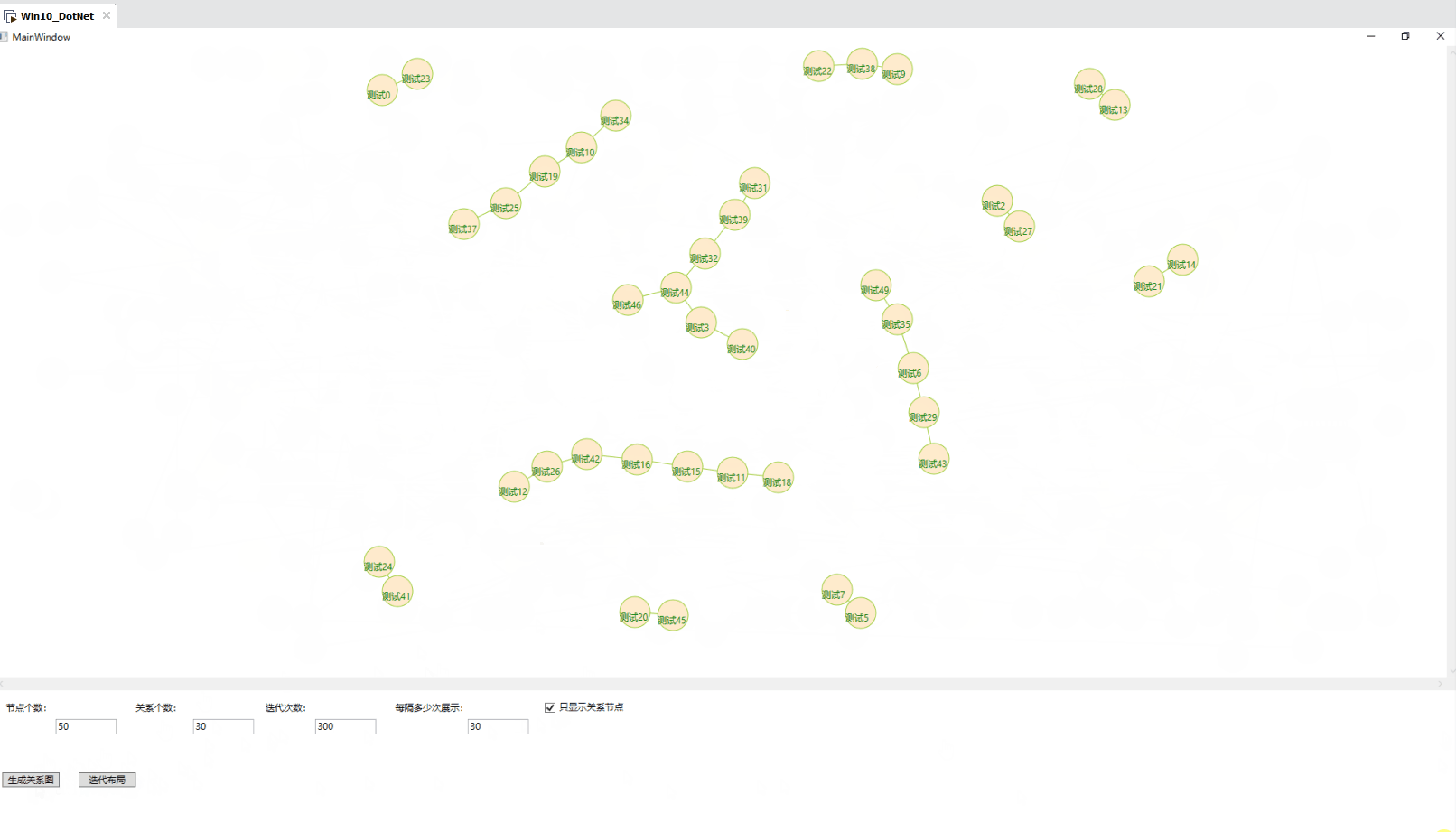
2.5 缺点
- 无法完全避免线压盖的情况
- 当节点和关系较多时会出现异常,需要扩展画布
- 总是有节点在两个不同位置上来回振动,虽然不会收敛,但是来回振动时的配置通常也最终可达到某种稳定的状态
- 当前博主暂未集成退火算法,需要随着迭代次数的增加,慢慢的需要微调,不能统一的使用调整的步幅,需要减少调整的步幅





















