前言
回顾下之前的章节:
- 第一章节中我们描述了整个框架的核心设计思路以及主要的文件架构
- 第二章节中我们基于一个简单的定时器OS实现了串口的数据打印,并完成了通用crc模块的设计和测试
- 第三章节中我们给出了真随机数和伪随机数的概念和代码示例,并在架构上对接口进行了重构
- 第四章节中我们回顾了FMC的基本知识,并给出了示例,后面我们将在设计IAP的时候再次使用到FMC
- 第五章节中我们使用ADC和DMA搭建了一个通用的采样框架,并通过串口给出了采样的数据示例
本文我们将总结下DAC的基本使用方法,并通过DAC生成任意频率的正弦波,三角波和方波。
什么是DAC?
前面我们讲过了ADC是把模拟量转成数字量,那么DAC就是反过来,即把数字量转成模拟量。
DAC一般需要配置的内容包括:
- IO配置(时钟,模拟输入)
- DAC参数配置(触发源,附加噪声?,数据宽度)
- 中断和DMA(使能)配置
DAC的配置比较简单,直接给出代码:
STM32
void dac1_init(void)
{
DAC_InitTypeDef DAC_InitStructure;
GPIO_InitTypeDef GPIO_InitStructure;
RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOA, ENABLE);
RCC_APB1PeriphClockCmd(RCC_APB1Periph_DAC, ENABLE);
GPIO_InitStructure.GPIO_Pin = GPIO_Pin_4;
GPIO_InitStructure.GPIO_Mode = GPIO_Mode_AIN;
GPIO_Init(GPIOA, &GPIO_InitStructure);
DAC_DeInit();
DAC_StructInit(&DAC_InitStructure);
DAC_InitStructure.DAC_Trigger = DAC_Trigger_Software;
DAC_InitStructure.DAC_WaveGeneration = DAC_WaveGeneration_None;
DAC_InitStructure.DAC_OutputBuffer = ENABLE;
DAC_Init(DAC_Channel_1, &DAC_InitStructure);
/* enable DAC0 and set data */
DAC_Cmd(DAC_Channel_1, ENABLE);
DAC_SoftwareTriggerCmd(DAC_Channel_1, ENABLE);
DAC_SetChannel1Data(DAC_Align_12b_R, 0);
}GD32
void dac1_init(void)
{
rcu_periph_clock_enable(RCU_GPIOA);
rcu_periph_clock_enable(RCU_DAC);
gpio_mode_set(GPIOA, GPIO_MODE_ANALOG, GPIO_PUPD_NONE, GPIO_PIN_4);
dac_deinit();
/* software trigger */
dac_trigger_enable(DAC0);
dac_trigger_source_config(DAC0, DAC_TRIGGER_SOFTWARE);
/* no noise wave */
dac_wave_mode_config(DAC0, DAC_WAVE_DISABLE);
/* noise wave - triangle */
//dac_wave_mode_config(DAC0, DAC_WAVE_MODE_TRIANGLE);
//dac_triangle_noise_config(DAC0, DAC_TRIANGLE_AMPLITUDE_4095);
/* noise wave - lfsr */
//dac_wave_mode_config(DAC0, DAC_WAVE_MODE_LFSR);
//dac_lfsr_noise_config(DAC0, DAC_LFSR_BITS11_0);
dac_output_buffer_enable(DAC0);
/* enable DAC0 and set data */
dac_enable(DAC0);
dac_software_trigger_enable(DAC0);
dac_data_set(DAC0, DAC_ALIGN_12B_R, 0);
}DAC的噪声波
有两种方式可以将噪声波加载到 DAC 输出数据:LFSR 噪声波和三角波。
具体参见初始化中的配置项。
三角波的波形如下所示:

LFSR噪声波的波形如下所示:

DAC波形发生器
如何通过DAC产生任意频率的周期性波形?
对于一个周期性波形,实际上它是一个时间的函数,即:y=f(t)
抽象一把,我们要解决2个问题:
- x轴时间如何采样?
- y轴数据如何计算?
数学推导 - x轴
假设频率为f,周期为T(T=1/f),采样点数为M:
那么△t = T/M,当给定频率f时,M=1/(△t*f)
在软件逻辑中,△t是定时器周期,为已知变量。

【注:请复习下奈奎斯特定理】
数学推导 - y轴 方波
如下数学推导中,MAX为幅值。
y = 0 if p < M/2 else MAX

1HZ方波
数学推导 - y轴 三角波
y = p*MAX/(M/2) if p < M/2 else (M-p)*MAX/(M/2)

1HZ三角波
数学推导 - y轴 正弦波
正弦波可以用数学库中的sin函数来计算,但是比较费事,可以通过角度查表的方式来计算。
另外,由于sin函数包含负值,需要将数据向上平移到正值(+1)。
rad = 360*p/M
y = (sin_table(rad) + 1) * MAX/20-90°的sin函数表如下所示:
const float sinus_I_quarter[91] =
{
0.0000, 0.0175, 0.0349, 0.0523, 0.0698, 0.0872, 0.1045, 0.1219, 0.1392, 0.1564, // 00 .. 09
0.1736, 0.1908, 0.2079, 0.2250, 0.2419, 0.2588, 0.2756, 0.2924, 0.3090, 0.3256, // 10 .. 19
0.3420, 0.3584, 0.3746, 0.3907, 0.4067, 0.4226, 0.4384, 0.4540, 0.4695, 0.4848, // 20 .. 29
0.5000, 0.5150, 0.5299, 0.5446, 0.5592, 0.5736, 0.5878, 0.6018, 0.6157, 0.6293, // 30 .. 39
0.6428, 0.6561, 0.6691, 0.6820, 0.6947, 0.7071, 0.7193, 0.7314, 0.7431, 0.7547, // 40 .. 49
0.7660, 0.7771, 0.7880, 0.7986, 0.8090, 0.8192, 0.8290, 0.8387, 0.8480, 0.8572, // 50 .. 59
0.8660, 0.8746, 0.8829, 0.8910, 0.8988, 0.9063, 0.9135, 0.9205, 0.9272, 0.9336, // 60 .. 69
0.9397, 0.9455, 0.9511, 0.9563, 0.9613, 0.9659, 0.9703, 0.9744, 0.9781, 0.9816, // 70 .. 79
0.9848, 0.9877, 0.9903, 0.9925, 0.9945, 0.9962, 0.9976, 0.9986, 0.9994, 0.9998, // 80 .. 89
1.0000 // 90
};由于sin函数的对称性,91°~360°可以通过数学公式推导得到:
#define CIRCLE_QUARTER_1 1
#define CIRCLE_QUARTER_2 2
#define CIRCLE_QUARTER_3 3
#define CIRCLE_QUARTER_4 4
float sinus_lookup (unsigned int angle)
{
float sin_value;
unsigned int circle_quarter;
// correct angles outside the accepted angle range into 0 .. 359
if (angle > 359u)
angle = angle % 360u;
circle_quarter = 1 + (angle / 90u);
switch (circle_quarter)
{
case CIRCLE_QUARTER_1: // 00 .. 89
sin_value = sinus_I_quarter[angle];
break;
case CIRCLE_QUARTER_2: // 90 .. 179
sin_value = sinus_I_quarter[180 - angle];
break;
case CIRCLE_QUARTER_3: // 180 .. 269
sin_value = -sinus_I_quarter[angle - 180];
break;
case CIRCLE_QUARTER_4: // 270 .. 359
sin_value = -sinus_I_quarter[360 - angle];
break;
}
return sin_value;
}

1HZ正弦波

100HZ正弦波
程序设计
波形程序
我们通过一个0.1ms的定时器作为△t,在定时中断函数中执行绘图函数。
void plot_sin(uint32_t f, uint32_t delta_f)
{
/* 定时周期为T=1/delta_f, f=1/(pMax*T) */
static uint32_t point = 0;
uint32_t pMAX = delta_f/f;
uint32_t value = 0;
if (point++ > pMAX) point = 0;
value = (uint32_t)((sinus_lookup(360*point/pMAX)+1)*10000)*2047/10000;
dac_software_trigger_enable(DAC0);
dac_data_set(DAC0, DAC_ALIGN_12B_R, value);
}
void plot_triangle(uint32_t f, uint32_t delta_f)
{
/* 定时周期为T=1/delta_f, f=1/(pMax*T) */
static uint32_t point = 0;
uint32_t pMAX = delta_f/f;
uint32_t pMAX2 = pMAX/2;
uint32_t value = 0;
if (++point > pMAX) point = 0;
if (point < pMAX2)
{
value = point * 4095 / pMAX2;
}
else
{
value = (pMAX - point) * 4095 / pMAX2;
}
dac_software_trigger_enable(DAC0);
dac_data_set(DAC0, DAC_ALIGN_12B_R, value);
}
void plot_square(uint32_t f, uint32_t delta_f)
{
/* 定时周期为T=1/delta_f, f=1/(pMax*T) */
static uint32_t point = 0;
uint32_t pMAX = delta_f/f;
uint32_t pMAX2 = pMAX/2;
uint32_t value = 0;
if (++point > pMAX) point = 0;
if (point < pMAX2)
{
value = 0;
}
else
{
value = 0xFFF;
}
dac_software_trigger_enable(DAC0);
dac_data_set(DAC0, DAC_ALIGN_12B_R, value);
}GD32的定时器配置和中断:
void timer3_init(void)
{
timer_deinit(TIMER2);
rcu_periph_clock_enable(RCU_TIMER2);
timerx_init(TIMER2, 999, 9); // 100KHz 0.1ms
timer_interrupt_enable(TIMER2, TIMER_INT_UP);
nvic_irq_enable(TIMER2_IRQn, 1, 2);
}
void TIMER2_IRQHandler(void)
{
#ifdef DAC_WAVE_TEST
plot_sin(100, 10000);
//plot_triangle(1, 10000);
//plot_square(1, 10000);
#endif
timer_interrupt_flag_clear(TIMER2, TIMER_INT_FLAG_UP);
}兼容设计
#ifdef STM32
#define DAC0 DAC_Channel_1
#define DAC1 DAC_Channel_2
#define DAC_ALIGN_12B_R DAC_Align_12b_R
#define dac_software_trigger_enable(channel) DAC_SoftwareTriggerCmd(channel, ENABLE)
#define dac_data_set(DAC_Channel_1, align, value) DAC_SetChannel1Data(align, value)
#endif例行结果展示
1HZ方波
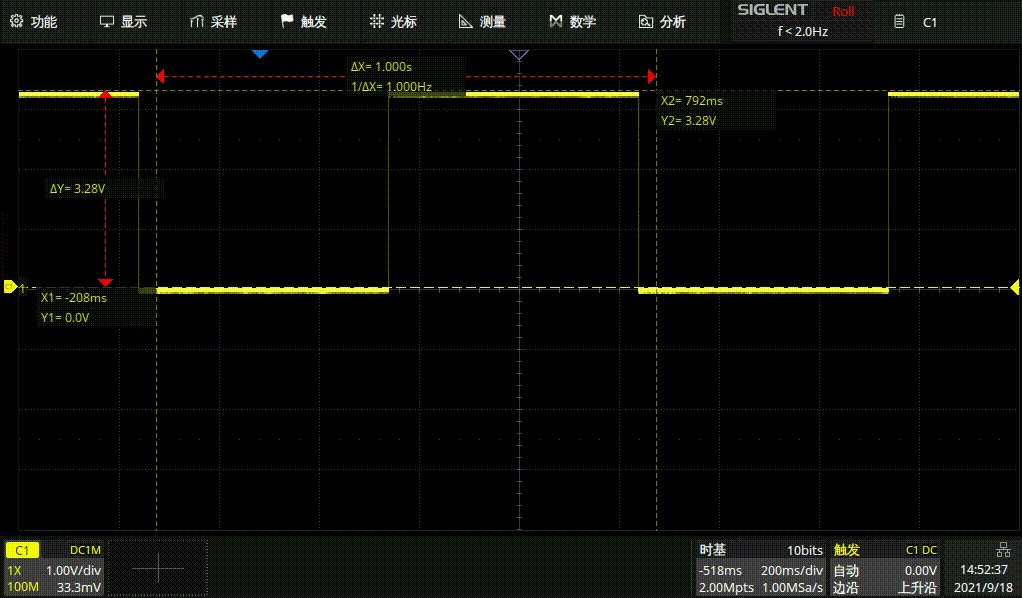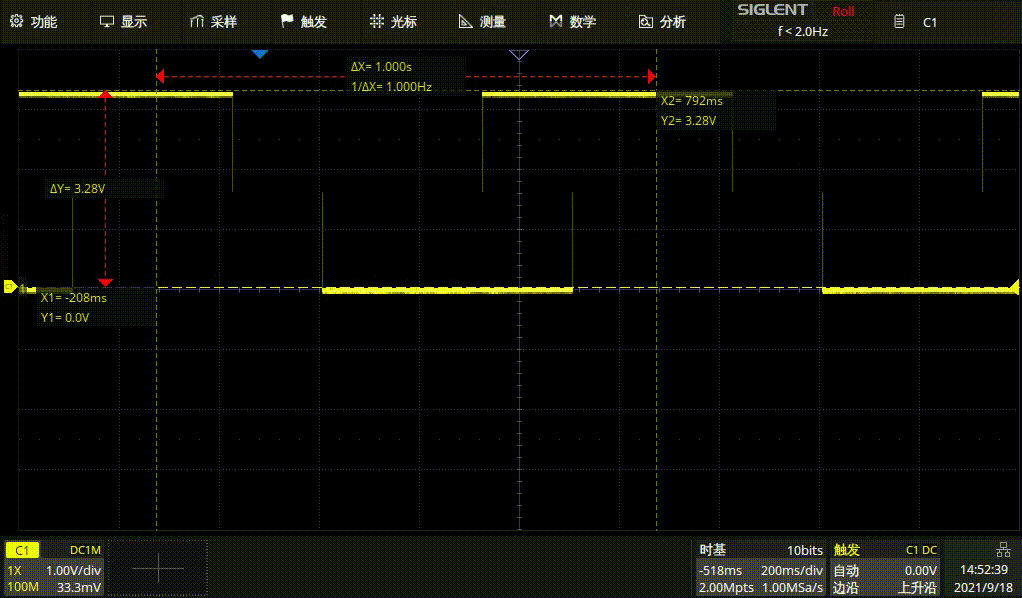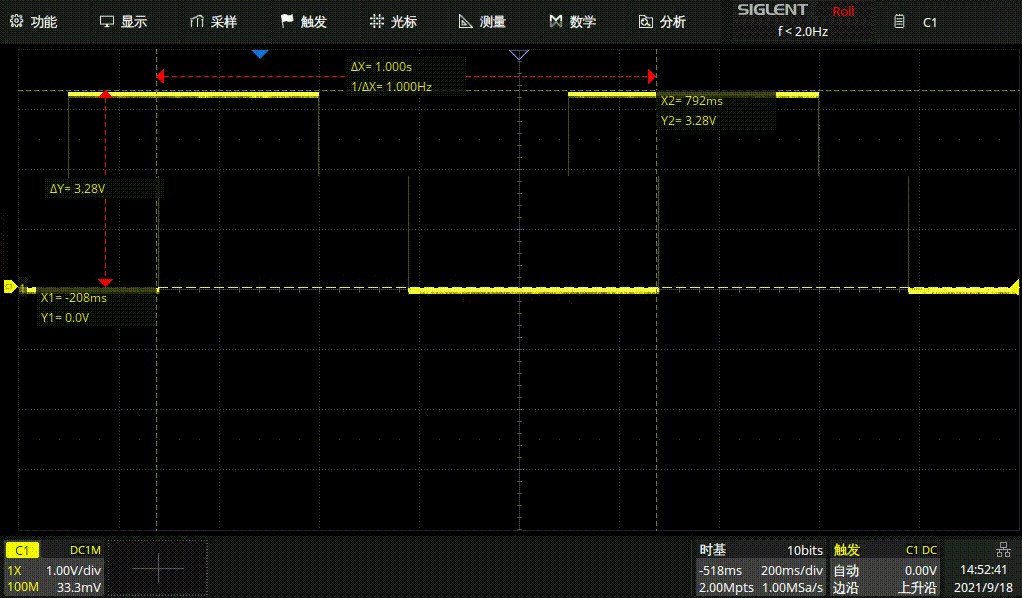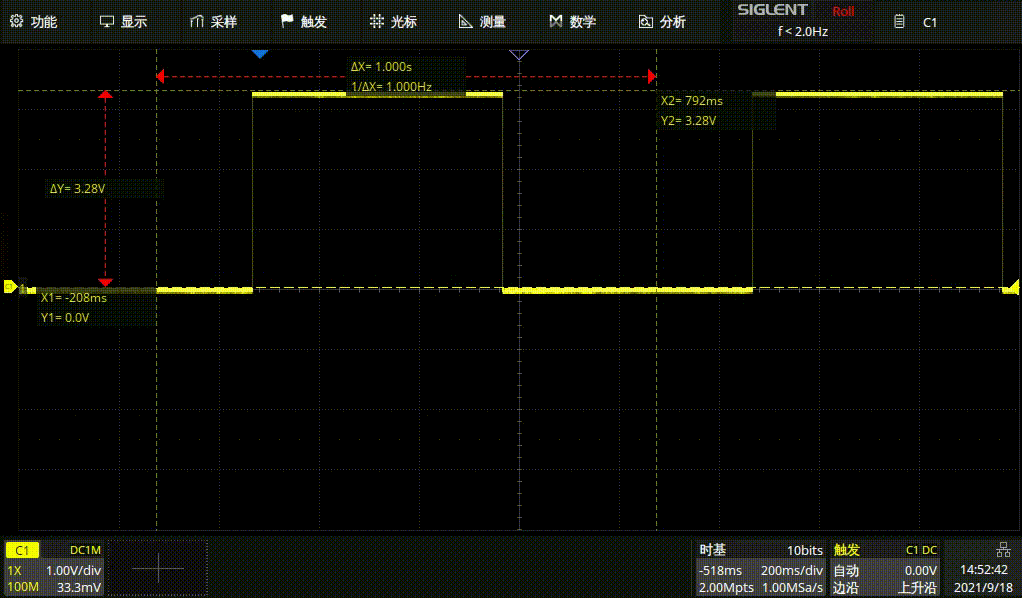
1HZ正弦波
1HZ三角波
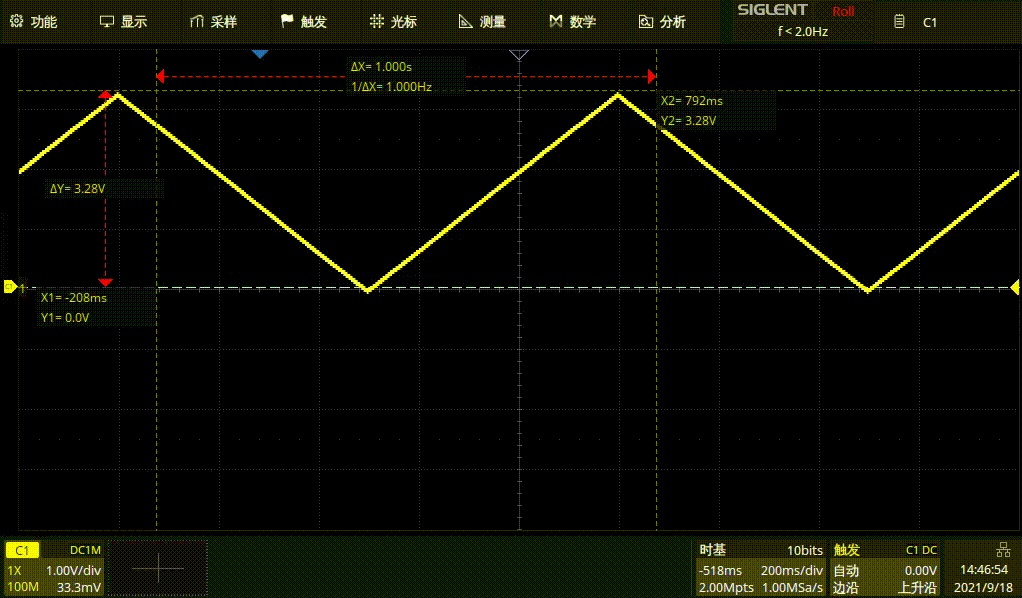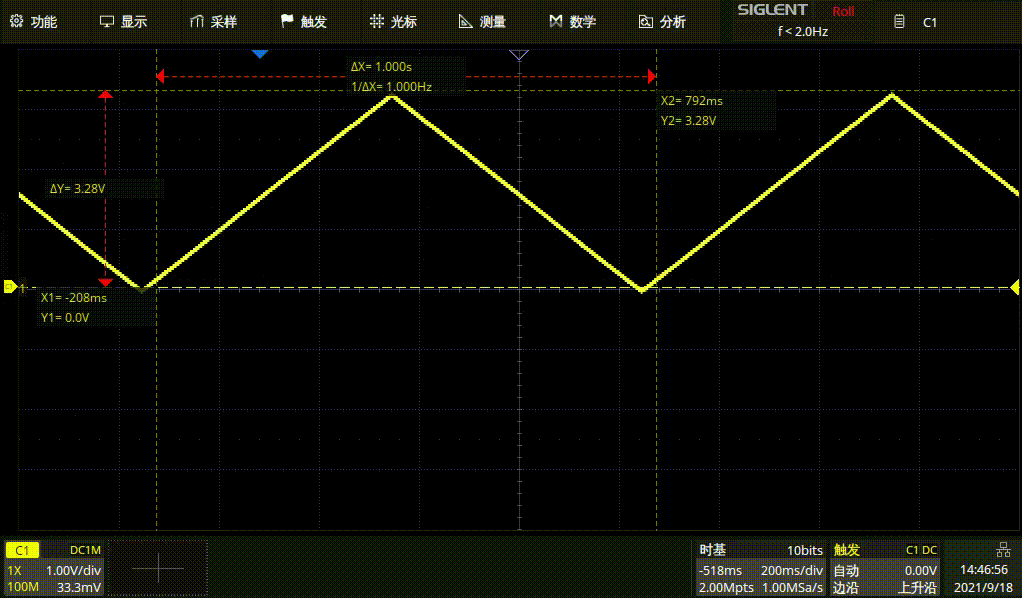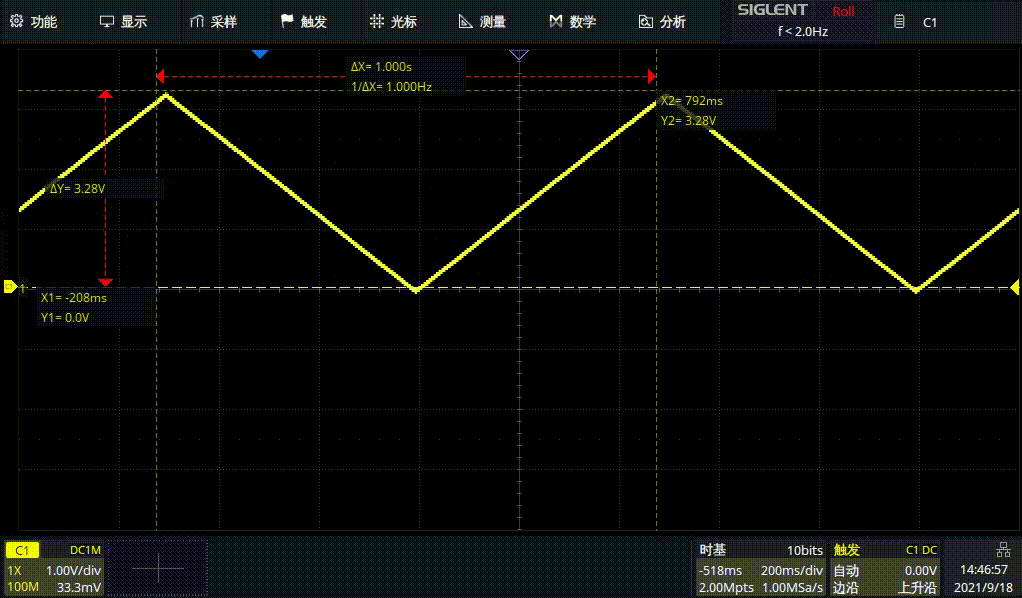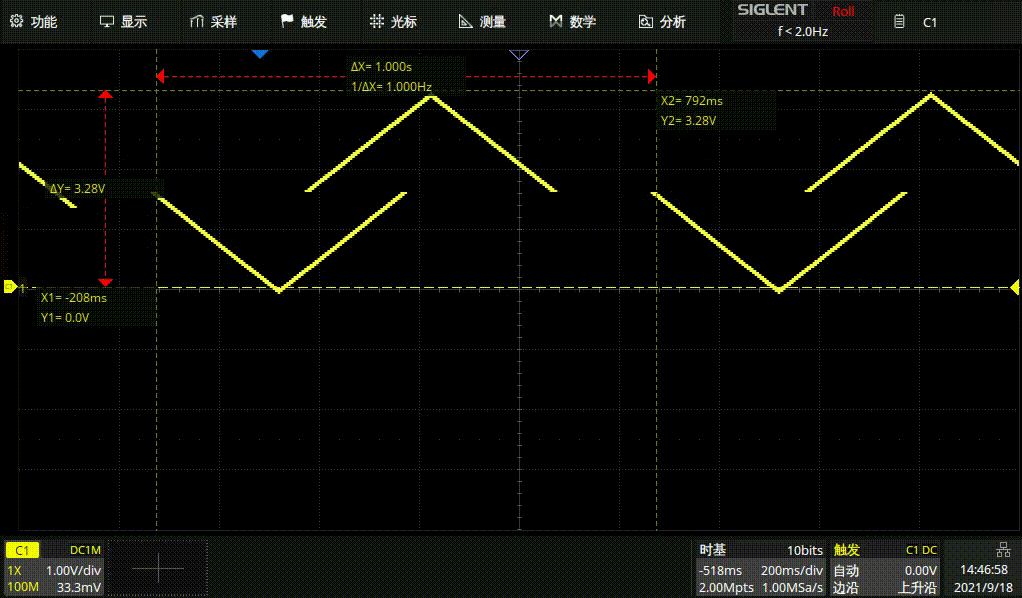
1HZ三角波
1HZ正弦波
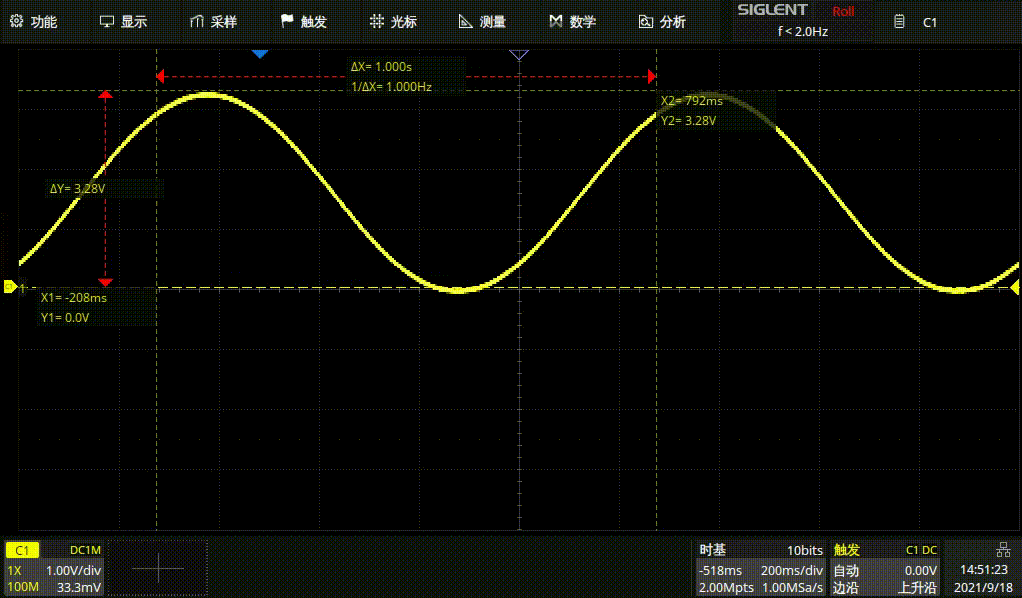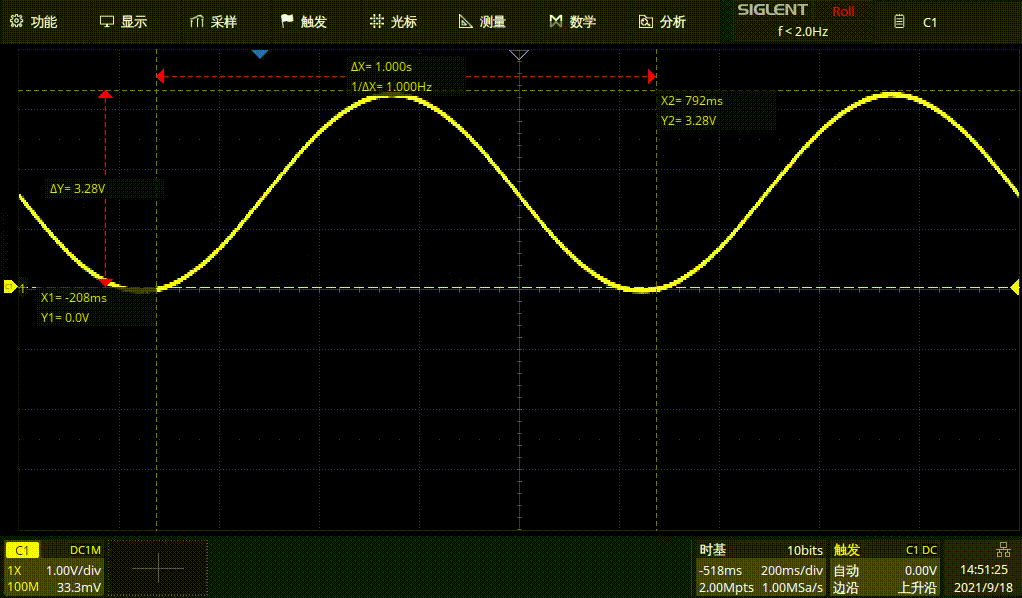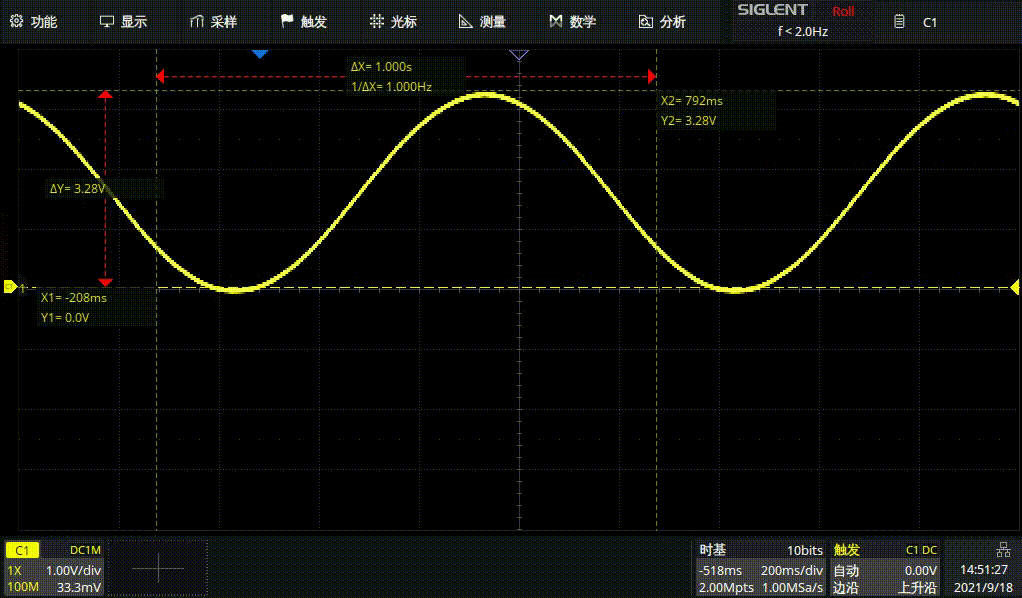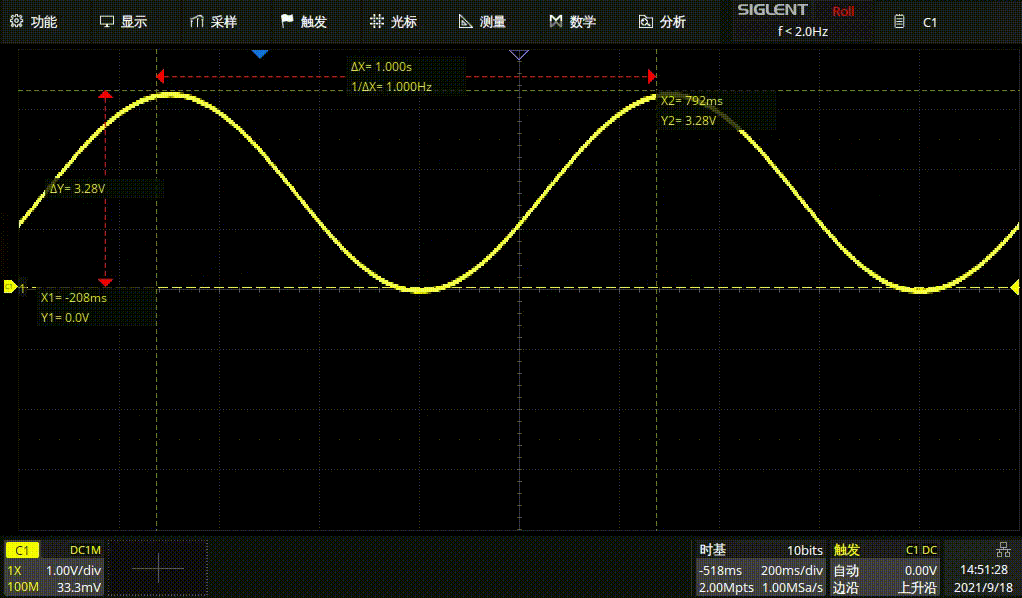
1HZ正弦波
100HZ正弦波
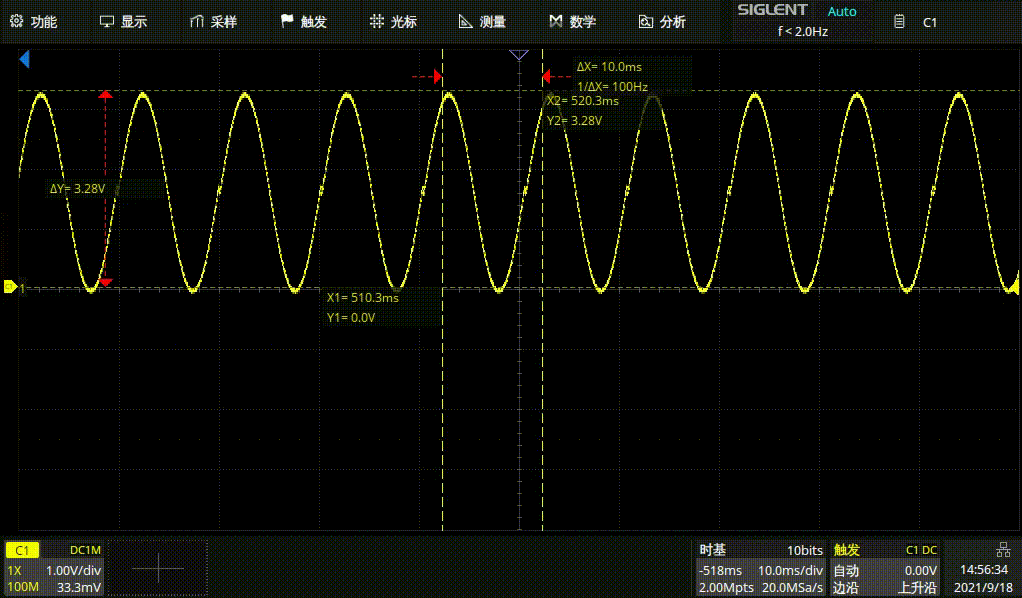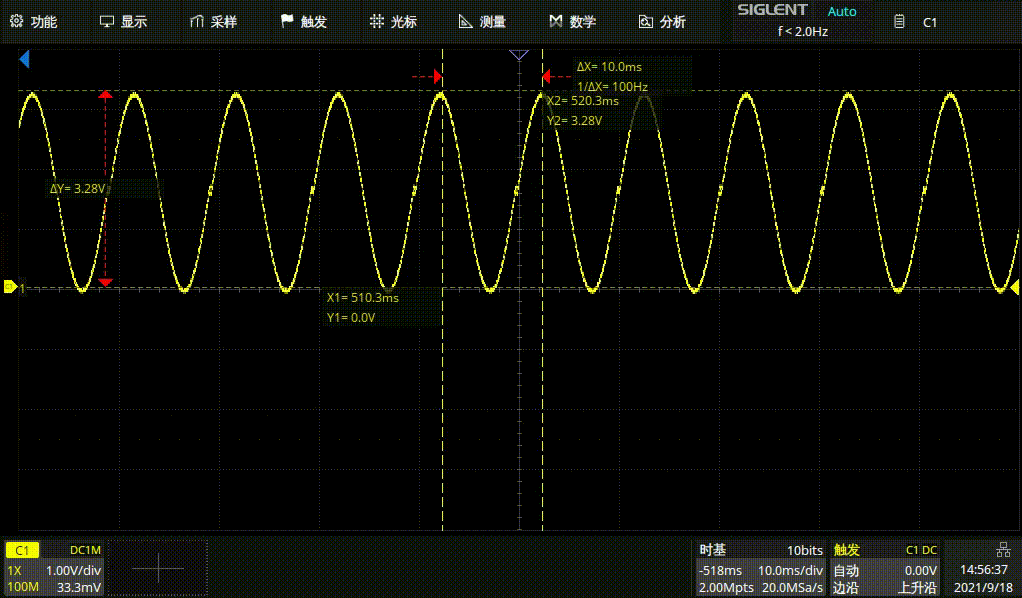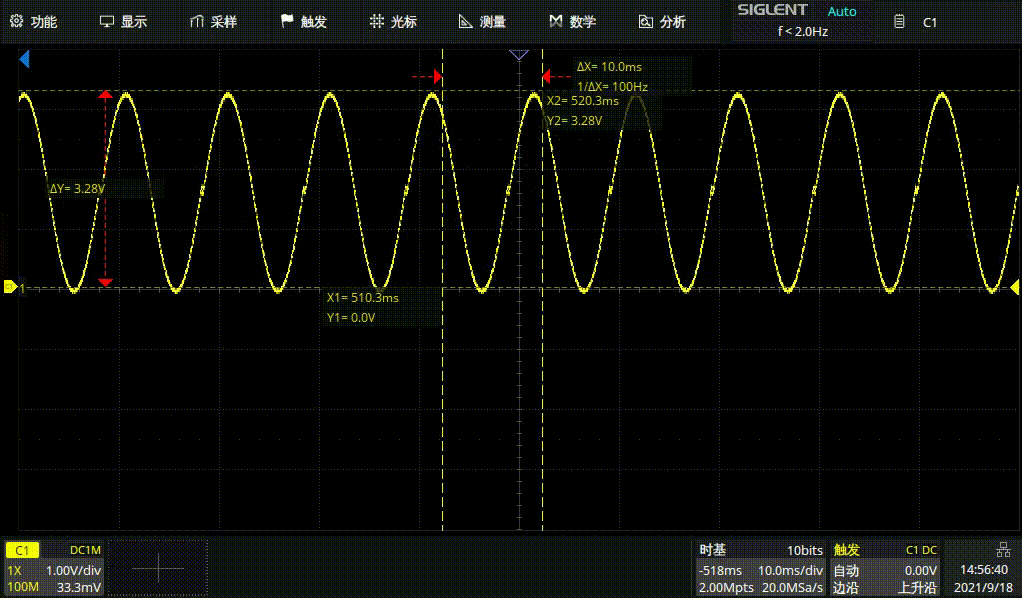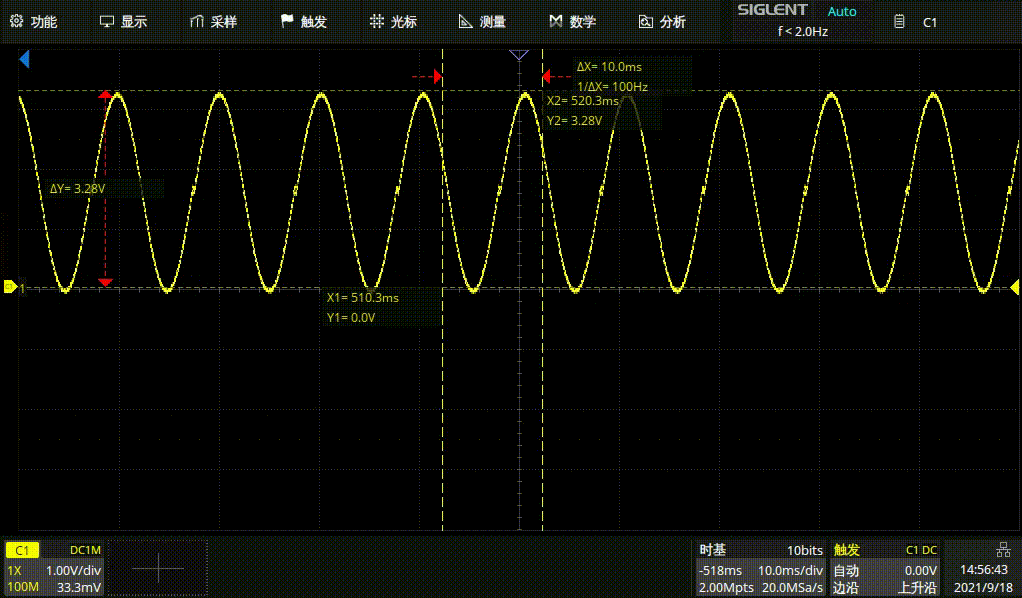
100HZ正弦波
GD正弦波和STM方波1HZ
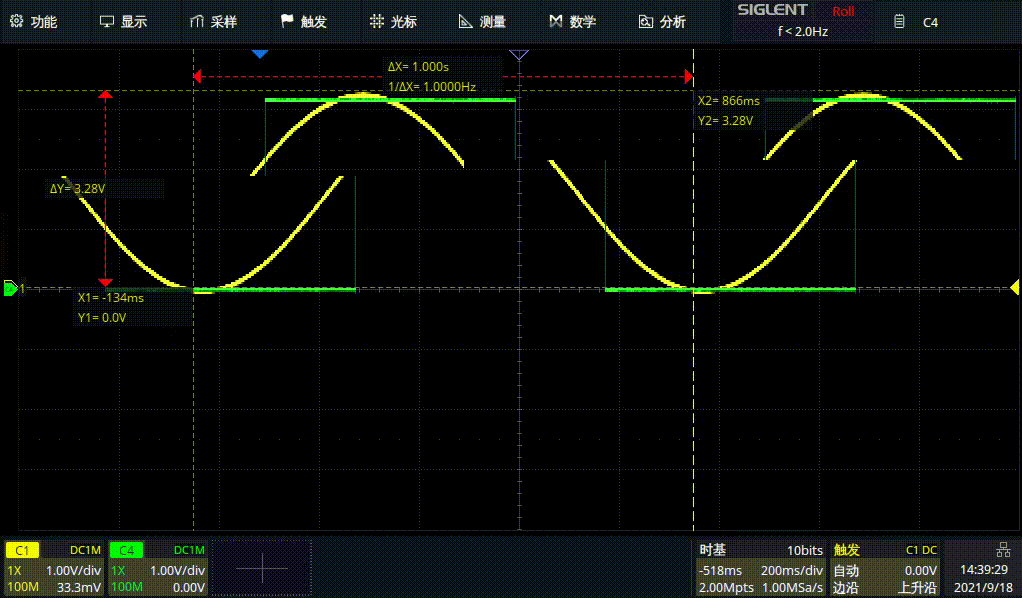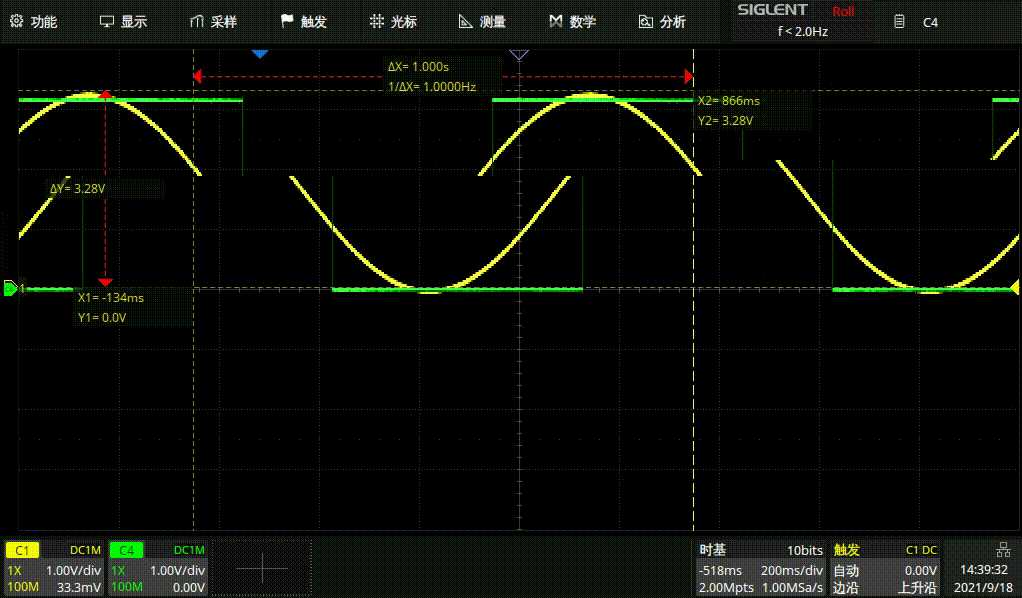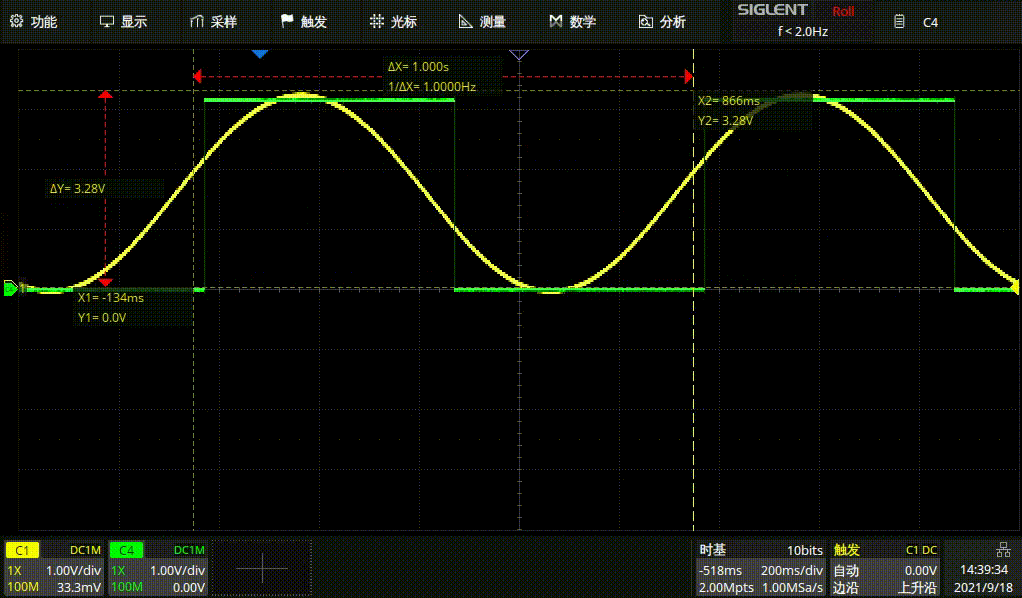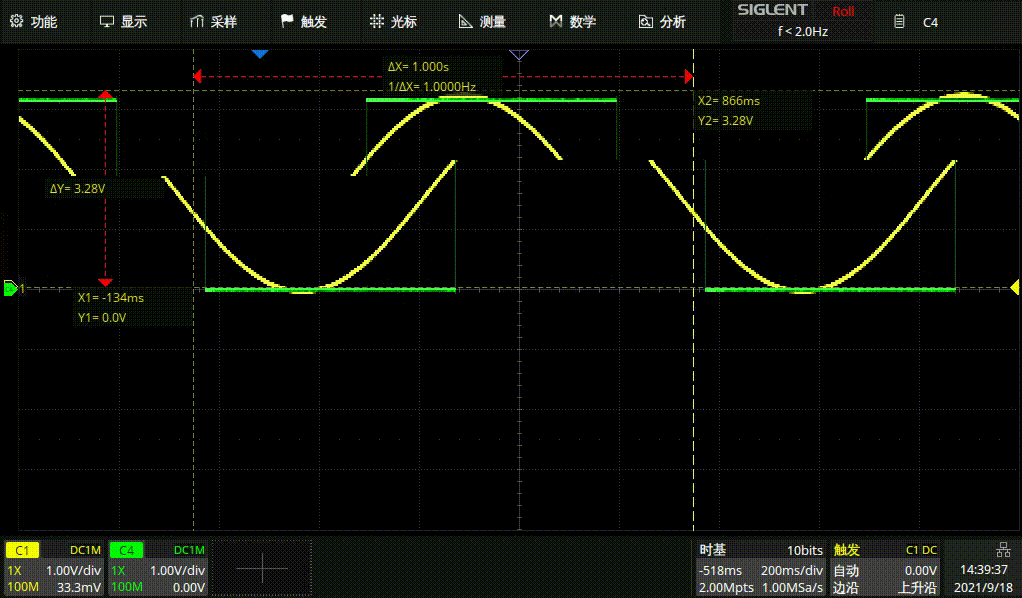
GD正弦波和ST
M方波1HZ
--EOF--





















