文章结构
- 1.卷积网络
- 1.1卷积基本原理
- 1.2 卷积的数学定义
- 1.3 卷积网络的前向与反向传播
- 1.4 卷积网络是如何做到简化模型的
1.卷积网络
一般的全连接网络存在什么问题。 我们可以发现,在我们使用全连接网络的时候,输入数据的形状往往会被忽视掉。我们输入进全连接网络中的数据,都会被拉成一个一维的数据。但是在类似图像处理的领域中,我们非常重视数据的形状,因为每个邻近像素点之间的有着紧密的关系,如果使用全连接网络来处理这样的图像,这些特征将无法被使用。
从前面对全连接网络的描述中,可以发现全连接网络试图去描述整个有向图中所有元素之间的关系,因为每一个变量都会有自己的参数,这可能会导致参数量剧增。在机器学习领域中的研究经验告诉我们,如果一个模型的参数过多往往或导致过拟合。因为试图描述所有的变量本身就不实际,而且一般的全连接网络通常是一个锤型,意味着每一层隐层中神经元的数量会随着隐层数量的增长而增长,这也会导致计算量的剧增,比如在图像处理中,一个200*200像素的图片就有40000个像素点,若连接至一个神经元数量大于40000的隐层,那么仅仅一层的参数数量就已经十分惊人。虽然理论上已经证实一个三层的简单神经网络理论上是可以拟合所有的函数,但是不具有可行性。而且在一些特殊的领域,比如图像识别,我们其实不需要关注所有的变量。举个栗子,我们想知道一张图片中的动物是猫猫还是狗狗,我们关注的只是一个区域的信息,而对这张照片其他其余的信息没有兴趣。这也就是我们为什么要用到卷积神经网络的原因之一。他更加的关注局部信息,同时也可以起到简化模型的作用。后面会详细来说,卷积神经网络为什么可以做到简化模型。
1.1卷积基本原理
通常卷积网络由以下部分组成:输入层,卷积层,池化层,输出层。现在先描述卷积神经网络是如何工作的,在逐一深入解释。现在假设我们有一张灰度图片,有m*n个像素,其中每一个位置的值代表的这个位置的亮度。输入层获得数据之后,将其传输给卷积层。卷积层中,我们引入一个“核”的概念(或者叫滤波器),这里的核和SVM中的核是两个完全不同的东西。这里的核和输入数据一样的有形状的,具体如图1所示:

那在卷积层中做的事情当然是将输入的数据与卷积核做卷积啦。卷积具体过程是什么?开始之前,思考一个问题,这个卷积核中的数代表的是什么呢?这其实就是卷积网络中的权重,换句话来说,核的参数对应了卷积网络的权重。接下来,开始卷积,我们将卷积核的中心(也就是图中的origin) 对准我们的输入图像的第一个位置,如图中绿色箭头所示。这样一来,卷积核的中心C5与输入数据中的I1相对应,C6对应I2,C8对应I6,依次类推。我们会发现卷积核的一些位置在输入数据中没有相对应的位置。这个时候我们需要填充这些空着的位置,这个过程就叫做padding。填充的方法有很多种,且每一种都有不同的效果。为了容易阐述,假设这里使用了零填充。零填充的就是用0去填充空的位置,前面提到过,原图像中的这些数字表示的是该像素点的亮度,意味着用0所填充的部分将呈现黑色。那么卷积就是原图像与卷积核对应的部分相乘在相加。这一次卷积的结果是一个数,我们将它记录下来,作为输出特征图的第一个元素。之后将卷积核的中心向右移动一个单位,移动的这一个单位就叫做步幅 / 步长(stride),换句话说就是每一次使用核的位置间隔,步长可以根据实际需要进行修改。我们用上述的步骤遍历完原图像中所有的元素(假设这里的步长为1 )就完成了卷积。如果步长为1 的话,那么最后的卷积结果的尺寸应该和原来的输入尺寸一样大。我们可以由此推断,加大步长会导致输出图像的尺寸变小,因为我们跳过了更多的元素。那我们怎么知道经我们的数据变成什么形状了呢?我们可以使用下面的两个公式来计算输出的高和宽。
在卷积层之后,紧跟的通常是一个池化层。池化通常分为两种,一种是最大池化,一种是平均池化。现在最常用的池化方式,就应该是最大池化。最大池化所做的事情就是在一个固定的范围内选取最大的像素点的值。我们同样使用一个叫做滤波器的东西来控制这个范围,若滤波器的尺寸为2,步长为 2,就意味着我们从相邻的四个像素中选择值最大那一个。同样的依次遍历卷积层的输出,得到池化层的输出。通常在一个完整的卷积网络中,会有多个卷积池化层。将经过多个卷积池化层的处理之后的数据做扁平化(变成一维)送进一个全连接网络中,得到最终的输出结果。
1.2 卷积的数学定义
在了解了卷积网络的基本工作方式和概念之后,我们可以稍微的思考深一点的问题。如何来理解卷积这个概念。数学的定义又是什么?通常卷积可以定义成cross-correlation 和 convolution 两种形式。它们之间的差距仅在于卷积核是否翻转了180度。换一句话来说,将卷积核翻转180度在做cross-correlation 就是convolution。那cross-correlation又是怎么定义的呢?我们可以结合前面用自然语言描述的卷积来思考。它无非就是将图片I 和 卷积核K 的对应元素相乘在相加。遍历所有在I 中的像素点,意味着就是要遍历所有的行和列。那么我们可已给出:
cross-correlation:
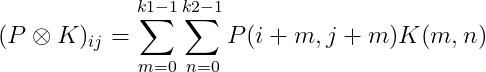
上述式子表达的是,图片P与卷积核K相互卷积之后,第I行,第j列的元素。为什么这里会有两个累加符号?两次累加其实是在遍历卷积核,一次遍历行,一次遍历列。然后根据cross-correlation和convolution的关系,我们可以给出数学上对于卷积的定义:
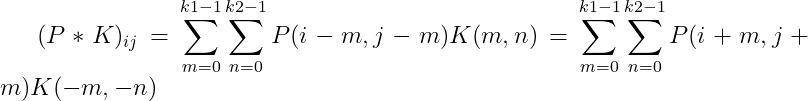
我们常用的TensorFlow和pytorch做卷积的时候就是使用的convolution的定义。
1.3 卷积网络的前向与反向传播
卷积网络中的前向和反向传播是如何进行的? 我们定义一个简单的卷积网络,来研究一下卷积网络的前向与反向传播的细节。
我们定义一个尺寸为 HW 的输入P,紧接着一个使用一个尺寸为k1*k2的卷积核K与输入发生卷积,设K的参数为
,得到输出特征图X之后,将特征图输入至一个激活函数
中之后得到最终的结果(暂不考虑池化层)。将层与层之间的关系画出来我们可以得到

上图可以理解成是这个简单卷积网络的前向传播过程!他和全连接的前向传播其实很类似。这里还是要再一次强调前向传播之所以叫前向传播,不是因为它不能向后运算,而是因为在这个网络中没有回路。
接下来看看反向传播应该如何计算。为了方便记录,我们假设模型输出结果是O,真实的标签是Y,设该网络的损失函数为 E = 。 反向传播的目的一定是通过调整网络参数来改变最终的输出。对于卷积网络而言,参数在卷积层中,我们需要知道,卷积层中的
的影响是如何一层一层传递到输出层的。从图中可以清楚的看到,数据P与卷积核发生卷积之后的得到了卷积层的输出特征图X,然后X被激活函数
接受,得到了最后的输出。从而我们可以从后向前,写出反向传播的表达式:
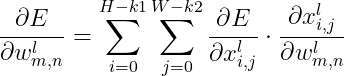
上述式中的 还有
中的
意思是在网络中的第几层。而下标表示的第几行和第几列。因为卷积网络的输入和卷积核都是有形状的!我们假设在第
层的误差已知,也就是
已知,用
来代表。那么我们现在最关心的就是
针对
求偏导的结果是多少?根据前面卷积的定义,我们可以很轻松的写出以下式子 (
是第
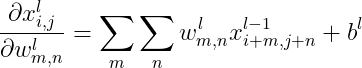
上述式是求 层的输出关于
层的
的偏导。而
层的输出等于
层的输出与
层的
的卷积。仔细看这个式子,我们会发现每一次的偏导,我们只针对一个
进行求导,因为在位置m,n上的
永远只有一个,这就意味着,其余的
不参与求导。那么整个过程就可以简化成下面的式子对
求偏导:
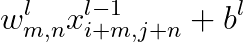
所以,我们可以将最终的求导结果整理成:
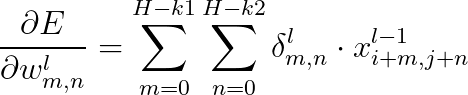
那么我们到这里可以看到上述式子其实就是我们先前定义的cross-corelation! 这就意味着,如果我们想求第 层的
对E的偏导,其实就是将第
层的损失与
层的输出做卷积(也可以说将
层的损失当做了一个卷积核。同样的,如果我们用convolution的定义我们只需要将“卷积核”翻转180度即可:
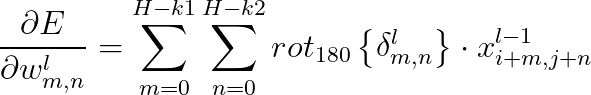
1.4 卷积网络是如何做到简化模型的
前面提到卷积网络可以对模型进行简化。那他具体是怎么做到的呢? 首先先明确一下,到底什么是简化。我认为的简化的意义是在保证性能的前提下,尽可能的减少参数。在一般的全连接网络中,我们可以发现每一个特征都会与隐层的神经元连接。通过什么连接的?权重矩阵!这不可避免的会出现大量的参数。而我们仔细观察一下卷积网络中,卷积层的工作原理,我们会发现,它其实是在复用权重!为什么?前面说到,卷积层的核的参数就可以理解成是卷积网络的权重,而他是通过卷积的方式将层与层连接起来的。然而每一层卷积核的大小是不变的。比如第层的卷积核大小是3*3那么这一层就只有9 个参数,不管输入有多少,他都会用这个九个参数去连接。这样就大大的减少了每一层的参数量。
第二,我们会发现卷积层与上一层是一种局部连接的方式,为了个更好的我们假设下图是一个4 * 4的灰度图像与一个2*2的卷积核做卷积,图中红色的框代表卷积核,红色的数组代表了卷积核参数,绿色的数字代表了灰度图像中的每一个像素点。

结合上图和卷积的原理,我们发现每一次卷积的输出只和卷积核覆盖的几个像素有关系,和其他的像素点没有关系,它只和局部的几个值连接,相对于全连接网络而言,卷积网络的连接就少很多。
综上,相对于全连接网络而言的话,卷积网络模型更加的简单,更不容易过拟合。因为参数的数量的被卷积核的大小限制,加上卷积的特点,使得连接相比于全连接网络而言大幅下降。





















