相信冒泡排序已经被大家所熟知,今天看了一篇文章,大致是说在面试时end在了冒泡排序上,主要原因是不能给出冒泡排序的优化。
所以,今天就写一下python的冒泡排序算法,以及给出一个相应的优化。OK,前言结束,步入正题:
首先,大家来看一下原始的python实现的冒泡排序算法:
def bubble_sort(nums):
for i in range(len(nums) - 1): # 这个循环负责设置冒泡排序进行的次数(比如说n个数,则只要进行n-1次冒泡,就可以把这个n个数排序好,对吧)
for j in range(len(nums) - i - 1):
"""
这里这个j呢就是控制每一次具体的冒泡过程,请你想一想,我们第一次冒泡需要冒几次,也就是说需要比较几次,
假如有三个数,那只需要两次就可以了,当下一次时,最后一个
已经是有序的了,所以说少冒泡一次,所以这里j每次都会减去i的值,即不用冒“无用之泡泡”
"""
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
return nums
盗用个图,动态展示一下冒泡排序过程:
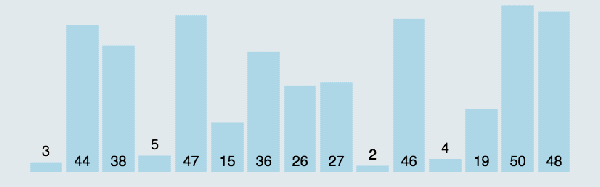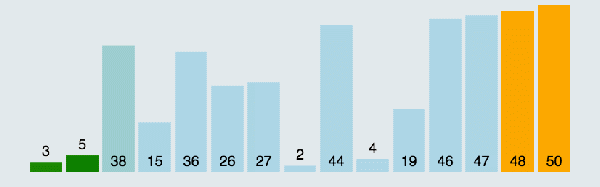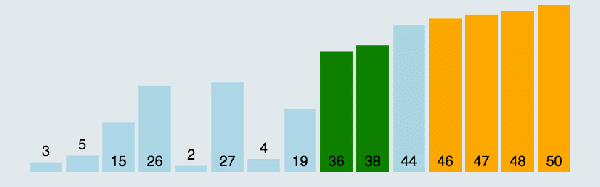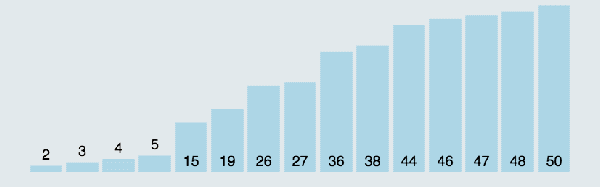
好了,终于说完原始的泡泡算法了,不对,是冒泡算法,接下来大家想一想,原始的冒泡算法存在什么问题呢?(思考ing)
相信聪明的你已经发现,这里我就帮你们说一下好了:
假设现在有一个数组[6,1,2,3,4,5],当我们进行完第一次冒泡排序过程后变为[1,2,3,4,5,6],这时候数组已经变成有序的了,程序要是再继续循环岂不是一直在做无用功,那怎么知道数组已经是有序的了呢?计算机又不跟你我一样能眼观大局,它看不到怎么办呢,于是它就再试一次呗,接下来再进行一次冒泡排序,1和2, 2和3, 3和4, 4和5, 5和6(好累,幸亏就tm六个数)依次冒泡,计算机好奇的发现,咦?奇了怪了,这次比较怎么没有一个数动一动,他们都那么懒啊,于是计算机就想,既然他们那么懒,我也不管了,老子不干了!于是乎,排序程序截止了,之后计算机惊奇的发现,输出的结果竟然排好序了!(心想,还TMD真排好了,我是谁,我在哪?)
OK,现在没计算机的事情了,需要大家帮它想一下,为什么它罢工之后反而还能输出正确结果,可以看出,当任意两个数字之间都没有发生交换,这代表着什么?这代表着任意两者之间都是有序的了啊!这代表着什么???这不就代表着这个列表已经是有序的了嘛(心想你si不si傻,这还要问,难道任意两者间有序你想不cu来人家列表已经有序了吗!!!)
到这里,终于可以放大招了,下面请看我们的冒牌排序优化版,不对是冒泡排序!!!(差点剧透了都。。。)
def bubble_sort(nums):
for i in range(len(nums) - 1):
ex_flag = False # 改进后的冒泡,设置一个交换标志位
for j in range(len(nums) - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
ex_flag = True
if not ex_flag:
return nums # 这里代表计算机偷懒成功 (〃'▽'〃)
return nums # 这里代表计算机没有偷懒成功 o(╥﹏╥)o
好了,上面的程序就不多做解释了,大家都是成年人,肯定能看懂的啦。
下面是福利时间,附赠大家一个冒牌排序,竟然有人声称这是冒泡排序,我是不能忍了,下面看代码:
def fake_bubble(num): # 这个是伪冒泡排序!!!
count = len(num)
for i in range(count):
for j in range(i+1, count):
if num[i] > num[j]:
num[i], num[j] = num[j], num[i]
return num
好了,来分析分析,这哪是冒泡排序啊,这不是赤裸裸的耍流氓嘛,从程序中可以看出,它的每一次循环,只是从未排序序列中取出第一个数,之后就拿这个数来依次和它后面的数相比,当然,在比较的过程中第一个数可能会变成另一个数(这实质性原因是因为它比后面的数大),但是不变的是每次都是未排序序列中第一个位置上的数依次和后面的数进行比较(这哪是冒泡啊,你是要累死第一个位置上的数吗,以后谁都不想当第一了)。这个程序只是每次都从未排序的序列中取出一个最小值,放在已排序序列的最后面,就是这样暴力,再次声明这不是冒泡排序!打假结束,收工~























