MP:matching pursuit匹配追踪
OMP:正交匹配追踪
主要介绍MP与OMP算法的思想与流程,解释为什么需要引入正交?
!!今天发现一个重大问题,是在读了博主的正交匹配追踪(OMP)在稀疏分解与压缩感知重构中的异同,之后一脸懵逼,CS中的稀疏表示不就是把信号转换到另一个变换域中吗?怎么跑出来一个稀疏分解里面又有MP和OMP算法!!后来发现原来稀疏分解先于压缩感知提出,信号稀疏表示的目的就是在给定的超完备字典中用尽可能少的原子来表示信号,可以获得信号更为简洁的表示方式,从而使我们更容易地获取信号中所蕴含的信息,更方便进一步对信号进行加工处理,如压缩、编码等。后面的学者用稀疏分解的思想应用于压缩感知重构中。其实两者解决的问题是一样的。
从数学模型来入手分析这个问题:
1)稀疏分解要解决的问题是在冗余字典A中选出k列,用这k列的线性组合近似表达待稀疏分解信号y,可以用表示为y=Aθ,求θ。
2)压缩感知重构要解决的问题是事先存在一个θ和矩阵A,然后得到y=Aθ(压缩观测),现在是在已知y和A的情况下要重构θ。
看到了没?实际上它们要解决的问题都是对已知y和A的情况下求y=Aθ中的θ。
上面各式中,A为M×N矩阵(M>>N,稀疏分解中为冗余字典,压缩感知中为传感矩阵A=ΦΨ,即测量矩阵Φ乘以稀疏矩阵Ψ),y为M×1的列向量(稀疏分解中为待稀疏分解信号,压缩感知中为观测向量),θ为N×1的列向量(稀疏分解中为待求分解系数,压缩感知中为信号x的在变换域Ψ的系数,x=Ψθ)。
所不同的是,在稀疏分解中θ是事先不存在的,我们要去求一个θ用Aθ近似表示y,求出的θ并不能说对与错;在压缩感知中,θ是事先存在的,只是现在不知道,我们要通过某种方法如OMP去把θ求出来,求出的θ应该等于原先的θ的,然后可求原信号x=Ψθ。
其实MP也好,改进后的OMP也罢,最初提出都是面向稀疏分解的,当时还没有压缩感知的概念,只是后来压缩感知提出后将其引入到了压缩感知重构中,因为前面也说了,其实他们的本质是一样的,都是已知y和A的情况下求y=Aθ中的θ。
1.冗余字典与稀疏表示
作为对信号进行稀疏分解的方法之一,将信号在完备字典库上进行分解。即在字典中找到一组基来表示信号,而用一组特定基表达一个信号其实就是找到相应的一组展开系数。一组基表达信号的能力取决于信号的特性是否与基向量的特性相吻合。例如,光滑连续信号可以被傅里叶基稀疏的表达,但脉冲信号不行。再如,带有孤立不连续点的平滑信号可用小波基稀疏表达,但小波基在表达傅里叶频谱中有窄带高频支撑的信号时却是无效的。
现实世界中的信号经常包含有用单一基所不能表达的特征。对于这些信号,你或许希望可以选择来自不同基的向量(如用小波基和傅里叶基来联合表达一个信号)。因为你想保证你可以表达一个信号空间的所有信号向量,所以由所有可选向量组成的字典应该能够张成这个信号空间。然而由于这组字典中的向量来自不同的基,它们可能不是线性独立的,会造成用这组字典做信号表达时系数不唯一。然而如果创建一组冗余字典,你就可以把你的信号展开在一组可以适应各种时频或时间-尺度特性的向量上。你可以自由的创建包含多个基的字典。例如,你可以构造一组表达平方可积空间的基,这组基包含小波包基和局部余弦基。这样构造的字典可以极大地增加你稀疏表达各种特性信号的能力。
2.字典非线性近似
定义表达你的信号空间的归一化基本模块作为字典。这些归一化向量叫做原子。如果字典的原子张成了整个信号空间,那么字典就是完全的。如果有原子之间线性相关,那么字典就是冗余的。在大多数匹配追踪的应用中,字典都是完全且冗余的。
假设{φk}表示字典的原子。假设字典是完全且冗余的。使用字典的线性组合表达信号将是不唯一的。
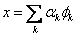
一个重要的问题是是否存在一种最好的表达方式,一种直观的最好方式是选择φk使得近似信号和原始信号有最大的内积,如最好的φk满足

即对于正交原子,为投影到由φk张成的子空间上的幅值。
匹配追踪的中心问题是你如何选择信号在字典中最优的M个展开项。
3.MP算法
》基本思想
MP算法的基本思想:从字典矩阵D(也称为过完备原子库中),选择一个与信号 y 最匹配的原子(也就是某列),构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,信号y可以由这些原子的线性和,再加上最后的残差值来表示。很显然,如果残差值在可以忽略的范围内,则信号y就是这些原子的线性组合。
》算法流程
用Φ={φk}表示一个原子归一化的字典,x表示信号。
(1)首先初始化残差e0=x;
(2)匹配追踪的第一步是从字典中找到与e0的内积绝对值最大的原子,表示为φ1;
(3)通过从e0减去其在φ1所张成空间上的正交投影得到残差e1;
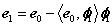
其中<e0, φ1>表示e0与φ1的内积。由于已经说明Φ为原子归一化的字典,即φ1为单位列向量,所以e0在φ1所张成空间上的正交投影可以表示为<e0, φ1>φ1 (由于为一个向量,所以e0在φ1所张成空间上的正交投影即为e0在φ1方向上的正交投影分量),若φ1不是单位列向量,则e0在φ1方向上的正交投影分量为<e0, φ1>φ1/(φ1Tφ1),其中上标T表示转置。
(4)对残差迭代执行(2)、(3)步;
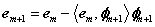
其中φm+1是从字典中找到与em的内积绝对值最大的原子。
(5)直到达到某个指定的停止准则后停止算法。
这里要从数学上说明一点:由于内积<em, φm+1>实际上为一个数(标量),所以
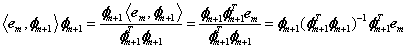
(分母中乘上φTm+1φm+1 ,一开始没想明白,注意这里的φm+1 是单位向量,则转置乘上自己是一个数值,也就是1)
若令P=φm+1 (φTm+1φm+1)-1φTm+1 ,(这里的P是用每次选择出的与残差内积最大的原子来计算的,而下面OMP中的P是用每次选择过的原子组成的矩阵来计算的!!!)则第(4)步的迭代公式为

注意矩阵P每次迭代都是不同的。
》提出一个问题
在描述MP算法时,有类似这样的话:在匹配追踪(MP)中,字典原子不是相互正交的向量。因此上面减去投影计算残差的过程中会再次引入与前面使用的原子不正交的成分。或者是:信号(残值)在已选择的原子进行垂直投影是非正交性的,这会使得每次迭代的结果并不是最优的而是次最优的,收敛需要很多次迭代。
那么如何理解什么是最优的,什么是次最优的?为什么不是正交的呢?
首先回顾下正交投影,一个向量(b)在另一个向量(a)上的投影:
p称为b在a上的正交投影,正交投影就是法线垂直于a的投影(不知道这种说法对不对,有待考究)实际上就是寻找在a上离b最近的点。如果我们把p看作是a的估计值,那么我们定义e = b - p,称e为误差(error)。 现在,我们的任务是找到这样的p,我们可以规定p = xa(x是某个数),那么e = b - xa,因为e与p也就是a垂直,所以有aT(b - xa) = 0,展开化简得到:
将x代入到p中,得到:
我们发现,如果改变b,那么p相对应改变,然而改变a,p无变化。
有了上面的背景知识,我们可以正式进入主题了,投影矩阵(projection matrix): p = Pb,显然这里有:
这个投影到底有什么用呢,从线性代数的角度来说,Ax = b并不一定总有解,这在实际情况中会经常遇到(m > n)。所以我们就把b投影到向量p上,求解Ax = p。 接下来,我们可以考虑更高维度的投影,三维空间的投影是怎么样的呢,我们可以想象一个三维空间内的向量在该空间内的一个平面上的投影:
我们假设这个平面的基(basis)是a1, a2.那么矩阵A = [a1 a2]的列空间就是该平面。假设一个不在该平面上的向量b在该平面上的投影是p,那么我们就有下面这个表达式p = x1a1+ x2a2= Ax,我们的任务就是找到这样的x。这里有一个关键的地方:e = b - Ax与该平面垂直,所以a1T(b - Ax) = 0且a2T(b- Ax) = 0.用矩阵的形式表达就是:AT(b - Ax) = 0. |
文献[3]中与文献[1]中所表示的算法流程符号略有不同,但意思是一样的,由于要借鉴这篇文章来解释上述提出的问题,所以先简要介绍一下该文献中所说明的MP的算法流程。
假定被表示的信号为y,其长度为n。假定H表示Hilbert空间(希尔伯特空间即完备的内积空间),在这个空间H里,由一组向量{x1,x2,...xn}成字典矩阵D,其中每个向量可以称为原子(atom),其长度与被表示信号 y 的长度n相同,而且这些向量已归一化处理,即 ‖xi‖=1,也就是单位向量长度为1。
(1)计算信号y与字典矩阵中每列(原子)的内积,选择绝对值最大的一个原子,它就是与信号y在本次迭代运算中最匹配的。用专业术语来描述:令信号y∈H,从字典矩阵中选择一个最为匹配的原子,满足

,(sup为上确界)r0表示一个字典矩阵的列索引。这样,信号y就被分解为在最匹配原子x

的垂直投影分量和残值两部分,即:

。
》之前想不明白为什么还要乘上xr0,联系一下傅里叶系数和傅里叶级数,此处y和xr0的内积是系数,而y是要由一组基的线性组合来表示的。

(2)对残值R1f进行步骤[1]同样的分解,那么第K步可以得到:

, 其中

满足

。(在别的参考文献中有形如这样的形式

,之前没有搞明白,其实也就是移项了而已)可见,经过K步分解后,信号y被分解为:

, 其中

。 我们要对信号进行稀疏表示,即在字典中找到一组最适合描述信号的基,把信号表示成这组基的线性组合。那为什么会造成不正交呢?举个例子说明一下:在二维空间上,有一个信号y被D=[x1, x2]来表达,MP算法迭代会发现总是在x1和x2上反复迭代,即

,这个就是信号(残值)在已选择的原子进行垂直投影的非正交性导致的。再用严谨的方式描述可能容易理解:在Hilbert空间H中,

,

,定义

,就是它是这些向量的张成的一个空间,MP构造一种表达形式:

;这里的Pvf表示 f在V上的一个正交投影操作,那么MP算法的第 k 次迭代的结果可以表示如下(前面描述时信号为y,这里变成f了,请注意):

如果

是最优的k项近似值,当且仅当

。由于MP仅能保证

,所以

一般情况下是次优的。这是什么意思呢?

是k个项的线性表示,这个组合的值作为近似值,只有在第k个残差和

正交,才是最优的。如果第k个残值与

正交,意味这个残值与fk的任意一项都线性无关,那么第k个残值在后面的分解过程中,不可能出现fk中已经出现的项,这才是最优的。而一般情况下,不能满足这个条件,MP一般只能满足第k个残差和xk正交,这也就是前面为什么提到“信号(残值)在已选择的原子进行垂直投影是非正交性的”的原因。如果第k个残差和fk不正交,那么后面的迭代还会出现fk中已经出现的项,很显然fk就不是最优的,这也就是为什么说MP收敛就需要更多次迭代的原因。不是说MP一定得到不到最优解,而且其前面描述的特性导致一般得到不到最优解而是次优解。那么,有没有办法让第k个残差与

正交,方法是有的,这就是下面要谈到的OMP算法。
简要概括就是我们是在找字典中的一组基进行线性组合后来作为f的最接近表示,每次的残差也就是Rkf会和f在当前所选择的基xk上的正交投影垂直,上式中的 fk是多个选择后的基的线性组合,不和残差项垂直。
4.OMP算法
》算法流程
在正交匹配追踪OMP中,残差是总与已经选择过的原子正交的。这意味着一个原子不会被选择两次,结果会在有限的几步收敛。OMP的算法如下
(1)用x表示你的信号,初始化残差e0=x;
(2)选择与e0内积绝对值最大的原子,表示为φ1;
(3)将选择的原子作为列组成矩阵Φt,定义Φt列空间的正交投影算子为

通过从e0减去其在Φt所张成空间上的正交投影得到残差e1;

(4)对残差迭代执行(2)、(3)步;
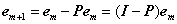
其中I为单位阵。需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵,因此每次都是不同的,所以由它生成的正交投影算子矩阵P每次都是不同的。
(5)直到达到某个指定的停止准则后停止算法。
OMP减去的Pem是em在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影,而MP减去的Pem是em在本次被选择的原子φm所张成空间上的正交投影。
》提出一个问题
OMP是怎么实现与所有选择过的原子正交的?
→施密特正交化
在现代数学引论中有学习过,但是和线性代数中的表达式不太一样,对两者进行了比较,发现其实本质是一样的。所选择的一组基是线性无关的,我们可以通过施密特正交化来将这组选择的基转换为正交基。


那么具体在OMP算法中是如何体现的?
文献[4]中给出了施密特(Schimidt)正交化的过程:

上面的的[x,y]表示向量内积,[x,y]=xTy=yTx=[x,y]。施密特正交化公式中的br实际上可写为:

分子之所以可以这么变化是由于[x,y]实际上为一个数,因此[x,y]x=x[x,y]= xxTy。
首先给出一个结论:
设OMP共从冗余字典中选择了r个原子,分别是a1,a2,……,ar,根据正交匹配追踪的流程可以知道待分解信号x最后剩余的残差eromp为

(式1)
该残差也可以表示为

(式2)
其中矩阵A为选择的r个原子组成的矩阵,e(r-1)omp为选择(r-1)个原子时的残差。
将选择的r个原子a1,a2,……,ar进行施密特正交化:

则残差eromp还可以写为

(式3)
(式1)一般出现在稀疏分解算法中,(式2)一般出现在重构算法中,(式3)是自己琢磨出来的(受到沙威的文档中提到的施密特正交化的启发,但沙威只限于向量情况下,详情可参见[6],此处相当于一个推广)
OMP分解过程,实际上是将所选原子依次进行Schimidt正交化,然后将待分解信号减去在正交化后的原子上各自的分量即可得残差。其实(式3)求残差的过程也是在进行施密特正交化。
有个关键问题还是要说的,分解后在所选择各原子上的系数是多少呢?答案其实也很简单,各个系数是(ATA)-1ATx,即最小二乘解,这个解是一个列向量,每一个元素分别是组成矩阵A的各原子的线性组合系数,这个在下一篇《正交匹配追踪(OMP)在稀疏分解与压缩感知重构中的异同》也会明确再次说明。
同理,若设MP共从冗余字典中选择了r个原子,分别是a1,a2,……,ar,根据匹配追踪的流程可以知道待分解信号x每次迭代后剩余的残差ermp为
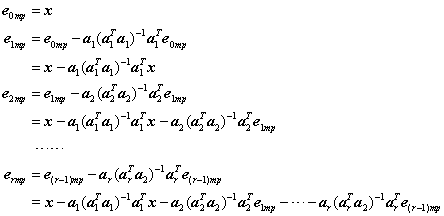
·比较式(3)的第2个等号表示的eromp与此处的ermp也可以体会出OMP与MP的区别吧。


























