在进行光学扫描时,会因为客观原因,导致扫描的图像位置不正,影响后期的图像处理,因此需对图像进行图像矫正工作。
1、图像倾斜矫正基础
图像倾斜矫正关键在于根据图像特征自动检测出图像倾斜方向和倾斜角度。目前常用的倾斜角度方法有:基于投影的方法、基于Hough变换、基于线性拟合,还有进行傅里叶变换到频域来进行检测的方法。
1.1 基于投影的倾斜矫正
基于投影的矫正方法,利用图像水平方向和垂直方向的投影特征来进行倾斜判断。主要用到投影的方差和均方差、投影特征矢量、梯度方向场等统计特性。
在图像投影中,一条直线沿着它的发现方向投影最长,沿着水平方向投影最短,此称之为Radon变换。定义:二元函数f(x,y)的投影是在某一方向上的线积分,例如f(x,y)在垂直方向上的线积分是f(x,y)在x方向上的投影,在水平方向上的线积分是在y方向上的投影,沿y'方向的线积分是沿x'方向上的投影。
图1 矩形函数在水平垂直方向和沿θ角方向的投影
投影可沿任意角度进行,通常f(x,y)的Radon变换是f(x,y)平行于y’轴的线积分,格式如下:
1.2 Hough变换法
Hough 变换是数字图象技术中一种有效的发现直线的算法 .它是先把直角坐标系的目标点映射到极坐标系上进行累积 ,即它是先使直角坐标系平面上任一直线上的所有点均累积到极坐标系的同一点集中去 ,然后通过寻找极坐标系中点集的峰值 ,来发现长的直线特征 .由于这种点集是通过累积统计得到的 ,因而能够容忍直线的间断 。
原理很简单:假设有一条与原点距离为S,方向角为0的一条直线,如下图所示:
证明过程如下:
在上图中有效根据三角形相似原理进行证明,找出线段与x,y,θ之间的关系:
然后我们再在直线上找一一点x1,y1只要证明也满足这个公式即可。在小三角形中:
进而:
所以直线上任意一点满足上述公式。
在x-o-y平面内可以看出(x1,y1)即属于直线L1又属于直线L2,且满足:
所以在x-o-y平面上的一点(x1,y1)对应于s-o-θ面上的的一条曲线,也就意味着在x-o-y平面内的直线对应s-o-θ存在很多条曲线上。同时由于一条直线上的点都满足公式:![clip_image002[18] 图像畸形矫正 python_数据结构与算法_17](https://s2.51cto.com/images/blog/202409/11112833_66e10e61500a968486.gif)
,即上述公式中我们知道s,θ为一个定值,所以意味着是个定点,所以所以x-o-y平面上处在一条直线上的点经过变换在S-O-θ平面上所得的曲线相交于一点。如下图所示
因此可以把x-o-y平面内直线的问题转化为S-O-θ平面内点的问题。
1.3、线性回归
如果我们有一系列相互独立的点,其近似分布在一条直线附近,我们可以通过线性回归拟合这条直线。
这条直线的一元线性回归模型为:
![clip_image004[8] 图像畸形矫正 python_人工智能_21](https://s2.51cto.com/images/blog/202409/11112834_66e10e6214a3c24381.gif)
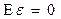
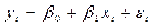
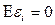
求Q的最小值:
由上式可得:
其中:
估计出了直线的斜率和截距,我们就可以估计出这条直线的方程了。
2、图像矫正算法实现
2.1 Rando变换算法实现
利用Radon变换检测直线倾斜角度的具体步骤为:
(1)用edge函数计算图像的边缘二值图像,检测出原始图像中的直线。
(2)计算边缘图像的Radon变换,对每一个象素为1的点进行运算(0-179度方向上分别做投影)
(3)检测出Radon变换矩阵中的峰值,这些峰值对应原始图像中的直线(上图中的四个亮点对应图3.9中的四条直线)。Radon变换矩阵中的这些峰值的列坐标θ就是与原始图像中的直线垂直的直线的倾斜角度,所以图像中直线的倾角为90-θ。
bw1=edge(l1,'sobel', 'horizontal');%用Sobel水平算子对图像边缘化
bw1=imcrop(bw1,[0 0 500 100]);%对图像进行剪切,保留图像中的一条直线,减小运算量
theta=0:179;%定义theta角度范围
r=radon(bw1,theta);%对图像进行Radon变换
[m,n]=size(r);
c=1;
for i=1:m
for j=1:n
if r(1,1)<r(i,j)
r(1,1)=r(i,j);
c=j;
end
end
end %检测Radon变换矩阵中的峰值所对应的列坐标
rot=90-c;%确定旋转角度
pic=imrotate(l1,rot,'crop');%对图像进行旋转矫正
2.2 Hough算法实现
(1)对图像进行边缘检测,这里选用了Sobel算子检测图像中水平方向的直线。
(2)假设图像对应于x-o-y空间,定义一个S-o-θ(θ角的范围为1-180)空间,对图像中象素为1的每一个点进行计算(应用公式(3.10)),做出每一个象素为1的点的曲线,同时把S-θ平面分成等间隔(1×1)的小网格,这个小网格对应一个记数矩阵。如图3.5所示,凡是曲线所经过的网格,对应的记数矩阵元素值加1,所以对原图像中的每一点进行计算以后记数矩阵元素的值等于共线的点数。我们可以认为记数矩阵中元素的最大值对应原始图像中最长的直线。
(3)检测出记数矩阵的最大的元素所对应的列坐标θ,θ即为这条直线的法线与X轴的夹角。因此我们可以通过θ角来确定直线的倾斜角度,进而对图像进行矫正。
Hough变换法矫正图像程序实现如下:
bw=edge(l,'sobel','horizontal');%检测图像边缘直线
[m,n]=size(bw);%计算图像大小
S=round(sqrt(m^2+n^2));%S可以取到的最大值
ma=180;%θ角最大值
r=zeros(md,ma);%产生初值为零的计数矩阵
for i=1:m
for j=1:n
if bw(i,j)==1
for k=1:ma
ru=round(abs(i*cos(k*3.14/180)+j*sin(k*3.14/180)));
r(ru+1,k)=r(ru+1,k)+1;%对矩阵记数
end
end
end
end
[m,n]=size(r);
for i=1:m
for j=1:n
if r(i,j)>r(1,1)
r(1,1)=r(i,j);
c=j;%把矩阵元素最大值所对应的列坐标送给c。
end
end
end
if c<=90
rot=-c; %确定旋转角度
else
rot=180-c;
end
pic=imrotate(l,rot,'crop'); %对图片进行旋转,矫正图像
下面是python版本的,里面讲解的比较详细
"""
Created on Tue May 30 13:59:20 2017
@author: Francesco Lacriola
"""
import numpy as np
from PIL import ImageDraw,Image
class Hough(object):
def __init__(self,image, n_theta, n_rho, plot_point):
self.image= image #immagine da analizzare
step=0 #
self.n_theta= n_theta #numero di angoli da analizzare per ogni punto
self.n_rho= n_rho #numero di intervalli di rho
thetas = np.deg2rad(np.linspace(-90.0, 90.0,self.n_theta)) #array contenente gli angoli da analizzare
width, height = self.image.shape
diag_len = np.ceil(np.sqrt(width * width + height * height)) # il rho massimo (la diagonale dell'immagine)
rhos = np.linspace(-diag_len, diag_len, self.n_rho+1) # i limiti degli intervalli
# Cache some resuable values
cos_t = np.cos(thetas) #calcola una volta tutti i cos degli angoli da analizzare e li salva in un array
sin_t = np.sin(thetas) #calcola una volta tutti i sin degli angoli da analizzare e li salva in un array
num_thetas = len(thetas)
accumulator = np.zeros((self.n_rho, num_thetas), dtype=np.uint64) #accumulatore
y_idxs, x_idxs = np.nonzero(self.image) # una lista di x ed y contenenti le cordinate dei punti bianchi (non zero)
# Vote in the hough accumulator
for i in range(len(x_idxs)): #cicla su tutti i punti bianchi (x è la x del punto corrente, y la sua y)
x = x_idxs[i]
y = y_idxs[i]
for t_idx in range(num_thetas): #cicla su tutti gli angoli da analizzare
# Calculate rho. diag_len is added for a positive index
rho = x * cos_t[t_idx] + y * sin_t[t_idx] #calcola rho
ind_rho = Hough.__binary_int__(rhos,rho) #approssima rho ad un indice all'interno dell'array degli intervalli
accumulator[ind_rho, t_idx] += 1 #assegna il voto
if plot_point is not None: #un controllo limite
plot_point(rho, np.rad2deg(thetas[t_idx%accumulator.shape[1]]), accumulator[ind_rho, t_idx], step) #aggiunge un punto al grafico
step+=1
self.accumulator=accumulator
self.thetas= thetas
self.rhos= rhos
def getHoughImage(self):
accmax= np.argmax(self.accumulator)
redacc=self.accumulator/self.accumulator[int(accmax/self.accumulator.shape[1])][accmax%self.accumulator.shape[1]]
return redacc
def getPatternImage(self):
image=np.zeros(np.shape(self.image))
image=Image.fromarray((image).astype('uint8'))
accmax= np.argmax(self.accumulator)
maxacc=self.accumulator[int(accmax/self.accumulator.shape[1])][accmax%self.accumulator.shape[1]]
draw = ImageDraw.Draw(image)
ord_accumulator= self.accumulator
ind_min=np.argmin(ord_accumulator)
i=int(ind_min/self.accumulator.shape[1])
j=ind_min%self.accumulator.shape[1]
while ord_accumulator[i][j]<maxacc:
rho = self.rhos[i]
theta = self.thetas[j]
y1=(rho/np.sin(theta))-(np.cos(theta)/np.sin(theta)*(np.shape(self.image)[1]-1))
y2=(rho/np.sin(theta))-(np.cos(theta)/np.sin(theta)*0)
#per trovare linee orizzontali if (y2-y1)/(-(np.shape(self.image)[1]-1)) >= -0.1 and (y2-y1)/(-(np.shape(self.image)[1]-1)) <=0.1:
draw.line((np.shape(self.image)[1]-1,y1, 0,y2), fill=int((ord_accumulator[i][j]/maxacc)*255))
ord_accumulator[i][j]=maxacc
ind_min=np.argmin(ord_accumulator)
i=int(ind_min/self.accumulator.shape[1])
j=ind_min%self.accumulator.shape[1]
i=int(accmax/self.accumulator.shape[1])
j=accmax%self.accumulator.shape[1]
rho = self.rhos[i]
theta = self.thetas[j]
y1=(rho/np.sin(theta))-(np.cos(theta)/np.sin(theta)*(np.shape(self.image)[1]-1))
y2=(rho/np.sin(theta))-(np.cos(theta)/np.sin(theta)*0)
#per trovare linee orizzontali if (y2-y1)/(-(np.shape(self.image)[1]-1)) >= -0.1 and (y2-y1)/(-(np.shape(self.image)[1]-1)) <=0.1:
draw.line((np.shape(self.image)[1]-1,y1, 0,y2), fill=int((ord_accumulator[i][j]/maxacc)*255))
return image
def __binary_int__(array,val):
assert val<= array[len(array)-1] and val>=array[0]
found=False
maxm=len(array)
start = int((maxm/2))
minm=0
if val == array[0]:
return 0
while not found:
if val<=array[start]:
maxm=start
start=int(((minm+start)/2))
elif val>array[start+1]:
minm=start
start=int(((maxm+start)/2))
else:
found=True
return start
2.3 线性回归算法实现
能够检测到图像上边缘的一系列的边界点,我们就可以通过最小二乘法拟合这条边界直线,从而确定图像的倾角。
具体方法如下:
(1)找出边界直线上的点(每列第一次由黑变白的点,且这一列的下两点还是白的话就可以判为边界点[6]),将其行坐标存入数组a即,列坐标存入数组b。
(2)通过最小二乘法拟和这条边界直线,计算出其斜率L。
(3)通过rot=atan(L),计算直线的倾斜角度,然后对其矫正。
[m,n]=size(l);
bw=im2bw(l,0.3);
%将图像二值化
t=1;s=1;
for j=144:1: n-144
for i=1:fix(m/4)
if bw(i,j)==0&bw(i+1,j)==1&bw(i+2,j)==1&bw(i+3,j)==1
%检测边缘点
c(t)=i;%边缘横坐标存入数组C
b1(s)=j;边缘纵坐标存入数组b1
break;
end
end
t=t+1;s=s+1;
end
x=0;y=0;x1=0;
for i=1:length(c)
x=x+c(i);
x1=x1+c(i)^2;
end
for i=1:length(b1)
y=y+b1(i);
end
y=y/length(b1);
x=x/length(c);
c1=x;
x=length(c)*x*x;
lxy=x1-x;
lxx=0;
for i=1:length(b1)
lxx=lxx+(c(i)-c1)*(b1(i)-y);
end
r=lxy/lxx;
%以上为计算直线参数
rot=atan(r);
%取余切
theta=rot*180/3.142;
%将弧度转换为角度
pic=imrotate(l,theta,'crop');

![clip_image002[4] 图像畸形矫正 python_数据结构与算法](https://s2.51cto.com/images/blog/202409/11112830_66e10e5e73a6981531.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)


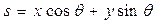
![clip_image002[4] 图像畸形矫正 python_人工智能_06](https://s2.51cto.com/images/blog/202409/11112831_66e10e5f6161b69877.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
![clip_image002[4] 图像畸形矫正 python_人工智能_07](https://s2.51cto.com/images/blog/202409/11112831_66e10e5f876d730696.gif)
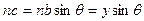
![clip_image002[6] 图像畸形矫正 python_线性回归_09](https://s2.51cto.com/images/blog/202409/11112831_66e10e5fde38437890.gif)
![clip_image002[8] 图像畸形矫正 python_数据结构与算法_10](https://s2.51cto.com/images/blog/202409/11112832_66e10e601667257895.gif)
![clip_image004[4] 图像畸形矫正 python_图像畸形矫正 python_11](https://s2.51cto.com/images/blog/202409/11112832_66e10e603e53913200.gif)
![clip_image002[12] 图像畸形矫正 python_线性回归_12](https://s2.51cto.com/images/blog/202409/11112832_66e10e606843b67610.gif)
![clip_image002[14] 图像畸形矫正 python_线性回归_13](https://s2.51cto.com/images/blog/202409/11112832_66e10e609ca5a48747.gif)
![clip_image002[6] 图像畸形矫正 python_人工智能_14](https://s2.51cto.com/images/blog/202409/11112832_66e10e60cd53239511.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
![clip_image002[16] 图像畸形矫正 python_数据结构与算法_15](https://s2.51cto.com/images/blog/202409/11112832_66e10e60f2ace48351.gif)
![clip_image004[6] 图像畸形矫正 python_图像畸形矫正 python_16](https://s2.51cto.com/images/blog/202409/11112833_66e10e612482985960.gif)
![clip_image002[8] 图像畸形矫正 python_python_18](https://s2.51cto.com/images/blog/202409/11112833_66e10e61802f461315.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
![clip_image002[10] 图像畸形矫正 python_数据结构与算法_19](https://s2.51cto.com/images/blog/202409/11112833_66e10e61af1aa271.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
![clip_image002[20] 图像畸形矫正 python_python_20](https://s2.51cto.com/images/blog/202409/11112833_66e10e61d9eeb78303.gif)


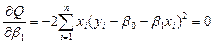

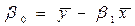
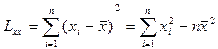
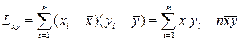

![clip_image002[12] 图像畸形矫正 python_线性回归_33](https://s2.51cto.com/images/blog/202409/11112836_66e10e644d29831257.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)





















