逻辑回归(对数几率回归)
逻辑回归是一种分类算法,不是回归算法,因为它用了和回归类似的思想来解决了分类问题。
一句话总结逻辑回归:“逻辑回归假设数据服从伯努利分布,通过极大似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的”。
1.广义线性模型
我们先来看看线性回归模型:
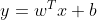
但是假设我们认为实例所对应的输出标记是在指数尺度上变化,那么就可以将输出标记的对数作为线性模型逼近的目标:

这就是“对数线性回归”,它实际上是试图让
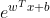
逼近y,其是形式上是线性回归,实际上是在求输入空间到输出空间的非线性函数映射。这里的对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用。更一般地,考虑单调可微函数

,另:

这样得到的模型称为“广义线性模型”,其中函数
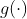
称为“联系函数”。显然,对数线性回归是广义线性模型在

时的特例。
如上讨论了如何使用线性模型来进行回归学习,但是如果要做的是分类任务该怎么办?下面介绍如何由“广义线性模型”引出逻辑回归模型。
我们只需要找到一个联系函数,将分类任务的真实标记y与线性回归模型的预测值联系起来。
考虑二分类问题,其输出标记

,而线性回归模型的预测值

是实数值,于是我们需要将实数值z转换为0/1值,可以使用单位阶跃函数:

但是该函数不连续,因此不能作为联系函数g,所以找到了一个能在一定程度上近似单位阶跃函数的“替代函数”,单调可微的对数几率函数(Logistic function),它能够将线性回归模型的预测值转化为分类任务对应的概率:
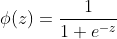
两者的图像如下图所示:

图1.单位阶跃函数与对数几率函数
对数几率其实是一种“sigmoid”函数,它将z值转化为一个接近0或1的y值:


若将y视为样本x作为正例的可能性,则1-y是其反例的可能性,两者的比值

称为“几率”,反映了x作为正例的相对可能性,对几率取对数则得到

,可以看出,上式其实是在用线性回归模型的预测结果去逼近真实标记的对数几率。所以该模型也被称作“对数几率回归”。
由于sigmoid函数的取值在[0,1]之间,所以可以将其视为类1的后验概率估计
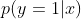
,所以我们把sigmoid函数计算得到的值大于等于0.5的归为类别1,小于0.5的归为类别0。

面经问题:
1. 为什么要使用sigmoid函数作为假设?
因为线性回归模型的预测值为实数,而样本的类标记为(0,1),我们需要将分类任务的真实标记y与线性回归模型的预测值联系起来,也就是找到广义线性模型中的联系函数。如果选择单位阶跃函数的话,它是不连续的不可微。而如果选择sigmoid函数,它是连续的,而且能够将z转化为一个接近0或1的值。
2.使用sigmoid函数背后的原理是什么?
2.逻辑回归的假设
任何的模型都是有自己的假设的,在这个假设下模型才是试用的。
逻辑回归的第一个假设是:假设数据服从伯努利分布。第二个假设为假设模型的输出值是样本为正例的概率。
所以整个模型可以描述为:

其中

=(w;b)为向量形式。
3. 逻辑回归的代价函数
为什么LR中使用交叉熵损失函数而不使用MSE损失函数?


所以,如果当前模型的输出接近0或者1时,σ′(z)就会非常小,接近0,使得求得的梯度很小,损失函数收敛的很慢.

(接下来就是根据给定的训练集,把参数w求出来。要找到w,首先要先定义代价函数(目标函数)。首先想到的就是模仿线性回归的做法,利用误差平方和来当做代价函数:
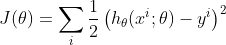
将

带入的话,会发现这是一个非凸函数,这就意味着代价函数有着许多的局部最小值,不利于求解。

而最大似然作为逻辑回归模型的损失函数,很容易得到参数的最优解(凸函数)。所以说选取的标准要容易测量,这就是逻辑回归损失函数为什么使用最大似然而不用最小二乘的原因。
(为什么MSE是非凸函数,有人能解答一下嘛))
3. 极大似然估计
逻辑回归与极大似然估计的关系:
最大似然估计就是通过已知结果去反推最大概率导致该结果的参数。极大似然估计是概率论在统计学中的应用,它提供了一种给定观察数据来评估模型参数的方法,即 “模型已定,参数未知”,通过若干次试验,观察其结果,利用实验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。逻辑回归是一种监督式学习,是有训练标签的,就是有已知结果的,从这个已知结果入手,去推导能获得最大概率的结果参数
,只要我们得出了这个参数,那我们的模型就自然可以很准确的预测未知的数据了。之前提到了

可以视为类1的后验概率,所以有:
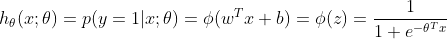
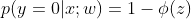
将上面两式写为一般形式:

接下来使用极大似然估计来根据给定的训练集估计出参数w:

为了简化运算,我们对上述等式两边取一个对数:

现在要求使得
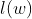
最大的

,在
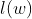
前面加一个负号就变为最小化负对数似然函数:

如此就得到了代价函数。让我们更好地理解这个代价函数:

等价于:
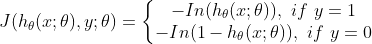

可以看出,如果样本的类别为1,估计值

越接近1付出的代价越小,反之越大。同理,如果样本的值为0的话,估计值

越接近于0付出的代价越小,反之越大。
4. 利用梯度下降法求解参数w
首先解释一些问什么梯度的负方向就是代价函数下降最快的方向,借助于泰勒展开:
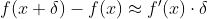

和
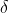
均为向量,那么两者的内积就等于:
当
时,也就是在

的负方向时,取得最小值,也就是下降的最快方向了。
梯度下降:


为学习率,用来控制步长

所以,在使用梯度下降法更新权重时,只要根据下式即可:
(
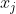
代表第j列特征,
代表第j个特征对应的参数)
当样本量极大的时候,每次更新权重都需要遍历整个数据集,会非常耗时,这时可以采用随机梯度下降法:
每次仅用一个样本点来更新回归系数,这种方法被称作随机梯度上升法。(由于可以在新样本到来时对分类器进行增量式更新,因此随机梯度算法是一个在线学习算法。)它与梯度上升算法效果相当,但占用更少的资源。
4.1 三种梯度下降方法的选择
- 批量梯度下降BGD(Batch Gradient Descent):优点:会获得全局最优解,易于并行实现。缺点:更新每个参数时需要遍历所有的数据,计算量会很大并且有很多的冗余计算,导致当数据量大的时候每个参数的更新都会很慢。
- 随机梯度下降SGD:优点:训练速度快;缺点:准确率下降,并不是全局最优,不易于并行实现。它的具体思路是更新没一个参数时都是用一个样本来更新。(以高方差频繁更新,优点是使得sgd会跳到新的和潜在更好的局部最优解,缺点是使得收敛到局部最优解的过程更加的复杂。?)
- small batch梯度下降:结合了上述两点的优点,每次更新参数时仅使用一部分样本,减少了参数更新的次数,可以达到更加稳定的结果,一般在深度学习中采用这种方法。
在实际应用时根据样本量的大小选择不同的梯度更新方法。
1)速度快,适合二分类问题
2)简单易于理解,直接看到各个特征的权重
3)能容易地更新模型吸收新的数据
缺点:
- 对数据和场景的适应能力有局限性,不如决策树算法适应性那么强
- 无法自动选择特
import numpy as np
def sigmoid(z): #
return 1.0 / (1 + np.exp(-z))
def logistic_regression(dataMatrix, labelMat):#n*m矩阵,n*1Vector
m, n = dataMatrix.shape
alpha = 0.0001
maxCycles = 500
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)
error = (labelMat - h)
weights = weights + alpha * dataMatrix.transpose()*error
return weights
def predict(inX,weights):
p = sigmoid(np.sum(inX*weights) )
return 1.0 if p>0.5 else 0.0
if __name__ =="__main__":
x1=list(range(1,51))
x1.extend(x1)
y1 = list(range(2,52))
y2 = list(range(0,50))
y1.extend(y2)
X = np.mat([x1,y1]).transpose()
z1 = [1 for _ in range(50)]
z1.extend([0 for _ in range(50)])
Z = np.mat(z1).transpose()
from matplotlib import pyplot as plt
plt.plot(x1[:50],y1[:50])
plt.plot(x1[50:],y1[50:])
plt.show()
#生成并且绘制测试数据集,如下面所示,转化为np矩阵
logistic_regression(X, Z)
# [[-1.06514021]
# [ 1.1820514 ]]






















