前言:
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络。 主要应用在 函数逼近,模式识别,分类,数据压缩(降低数据维度)
算法 优点:广泛的适应性和有效性
缺点: 训练速度慢,算法不一定收敛
这里主要结合乳腺癌例子,介绍一下BP算法。
目录
- 概述
- 算法原理
- 乳腺癌例子
一 概述
1.1 BP 算法

BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络。 整个网络,主要分为输入层,隐藏层,输出层三部分。
每个方框代表一个神经元, 神经元主要由 积分器和 激活函数组成

二 算法流程
算法主要分为两个部分
正向转播: 求损失函数,以及迭代终止判断条件
反向传播: 更新隐藏层权重系数V,以及输出层权重系数W
2.1 损失函数
2.1.1 输出层损失函数

其中
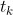
代表标签值
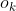
代表计算值
K: 代表输出层输出个数。
比如2分类,K可以设计成1个,也可以设计成多个,但是每个输出的标签是一样的。

2.1.2 展开至隐层
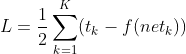
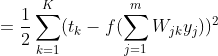
2.1.3 展开至输入层
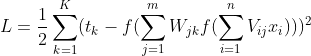
其中f代表激活函数,这里主要使用的是SigMoid函数:
重新上传取消

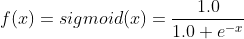

三 算法推导
最终是更新输入层至隐藏层的权重系数V,以及隐藏层到输出层的权重系数W
2.1 正向传播 计算误差(类似HMM中的前向算法)
输入层至隐藏层公式2
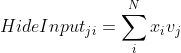
隐层的积分器到激活函数输出公式3
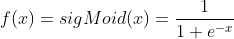
(HideOuput)
因为此刻的隐层输出需要作为下一层的输入,所以需要加上参数b,公式4
Y = np.vstack((hide_output,self.HideB )) 公式4
输出层输入,公式5
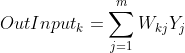
其中m是隐层神经元个数+1 (1是参数b)
输出层输出, 公式6
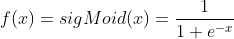
(Out_input)
假设值为Z,其导数为Z(1-Z)
最后得到当前的误差
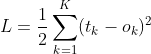
2.2 反向传播(类似HMM中的后向算法)
隐藏层到输出层的更新过程:

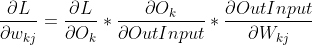
公式7
其中
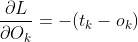
公式1
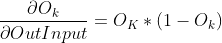
公式8
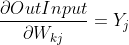
其中
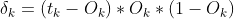
则
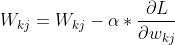
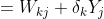
公式13
输入层到输出层的更新过程

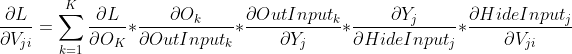
其中
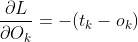
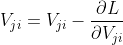
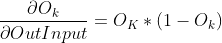
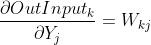
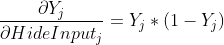
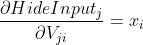
令A =
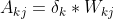
公式12
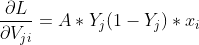
则
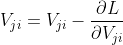
=
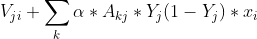
公式14
三 算法例子
数据集可以使用2种: 乳腺癌 和 LoadData 里面的
# -*- coding: utf-8 -*-
"""
Created on Wed Feb 26 11:20:16 2020
@author: chengxf2
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_breast_cancer
class BP():
"""
加载乳腺癌数据集,数据集总共有569个样本
训练集用了300个样本
Args
None
return
None
"""
def LoadCancerData(self):
cancer = load_breast_cancer()
X = cancer.data
Y = cancer.target
m,n = np.shape(X)
scaler = StandardScaler().fit(X)
X = scaler.transform(X)
trainNum = 400 ##70% 作为样本,
testNum = m- trainNum
A = np.ones((trainNum,1))
B = np.ones((testNum,1))
self.trainData = np.hstack((X[0:trainNum,],A))
self.trainLabel = Y[0:trainNum]
self.testData = np.hstack((X[trainNum:,],B))
self.testLabel = Y[trainNum:,]
print("\n 训练样本: ", trainNum, "\t 测试样本: ",testNum)
self.M, self.N = np.shape(self.trainData)
self.nHide = self.N+5 ##隐藏层的个数
self.V = np.random.rand(self.nHide, self.N) # 输入层到隐藏层的权重系数
self.W = np.random.rand(self.nOut, self.nHide+1) #隐藏层到输入层的权重系数
#self.trainData =np.hstack((A,B))
"""
加载数据集
Args
fileName
return
None
"""
def LoadData(self, filename):
dataList = []
labelList = []
BList = []
fr = open(filename)
for line in fr.readlines():
lineArr = line.strip().split()
dataList.append([float(lineArr[0]), float(lineArr[1])])
labelList.append(int(lineArr[2]))
BList.append([1.0])
scaler = StandardScaler().fit(dataList)
dataList = scaler.transform(dataList)
A = np.array(dataList,np.float)
B = np.array(BList)
self.trainData =np.hstack((A,B))
self.trainLabel = np.array(labelList,np.float)
self.M, self.N = np.shape(self.trainData) ##样本个数, 样本维度
self.V = np.random.rand(self.nHide, self.N) # 输入层到隐藏层的权重系数
self.W = np.random.rand(self.nOut, self.nHide+1) #隐藏层到输入层的权重系数
for i in range(self.M):
x = self.trainData[i,0]
y = self.trainData[i,1]
if self.trainLabel[i]==0:
plt.scatter(x,y,c='r')
else:
plt.scatter(x,y,c='g')
plt.show()
"""
S函数,导数是连续的,y(1-y)
args
x: 实数
return [0,1]
"""
def Sigmoid(self, x):
y = 1.0/(1.0+np.exp(-x))
return y
"""
sigMoid 函数的导数
Args
y: 输出值
return
dy: 导数
"""
def DSigmoid(self,y):
#print("y: ",y)
dy = np.multiply(y, (1.0 - y))
return dy
"""
前向传播
Args
None
return
sse: 所有样本,在各个输出结点上的误差总和
"""
def Forward(self):
hide_input= np.dot(self.V, self.trainData.T) #隐藏层输入NetJ 公式2
hide_output = self.Sigmoid(hide_input) #隐藏层输出 公式 3
self.Y = np.vstack((hide_output,self.HideB )) ##行顺序添加一个数组,增加一个参数B, 变成下一层的输入 公式4
out_input = np.dot(self.W, self.Y) #输出层输入, 公式5
self.out_output = self.Sigmoid(out_input) #输出层输出,公式6
self.err = self.trainLabel - self.out_output #输出层误差,Loss, 公式1
sse = np.sum(np.power(self.err, 2)) * 0.5
return sse
def __init__(self):
self.nHide = 50 #隐藏层神经元个数
self.nOut = 1 ##输出层神经元个数
self.V = None # 输入到隐藏层的矩阵
self.Y = None #隐藏层的输出
self.W = None # 隐藏层到输出层的权重
self.output = None #输出层的输出
self.maxIter = 50000 ##最大迭代次数
self.errMax = 0.001 ##误差上限
self.mc = 0.0 #动量因子
self.errlist = [] # 误差列表
self.delta = None #误差
self.alpha = 0.1 ##步伐
"""
训练
"""
def Train(self):
i = 0
self.HideB = np.ones((1,self.M)) #相当于隐藏层增加一个B
sse = 0.0
oldsse = np.inf
while i < self.maxIter:
sse = self.Forward() ##前向传导
#print("\n i: ",i, "\t sse: ",sse)
self.errlist.append(sse)
# 判断是否收敛至最优
if sse <= self.errMax:
self.iterator = i + 1
print("\n ************break *******",i)
break
Dout_put = self.DSigmoid(self.out_output) ##公式8 输出层的误差
delte_out = np.multiply(self.err,Dout_put) #公式9 delte参数
delte_w = np.dot(delte_out,self.Y.T) #公式7 输出层的w的偏导数
A = np.dot(self.W[:,:-1].T, delte_out) #公式11 隐藏层的误差
delte_hide = np.multiply( A, self.DSigmoid(self.Y[:-1,:])) #公式12 隐藏层的delte
delte_V = np.dot(delte_hide , self.trainData) # 公式10 隐藏层V的偏导数
if i == 0:
self.W = self.W+ self.alpha*delte_w #公式13 输出层的误差更新公式
self.V = self.V + self.alpha*delte_V #公式14 隐藏层的误差更新公式
else:
self.W = self.W + (1.0 - self.mc) * self.alpha * delte_w + self.mc * delte_wOld
self.V = self.V + (1.0 - self.mc) * self.alpha * delte_V + self.mc * delte_vOld
delte_wOld = delte_w
delte_vOld = delte_V
i = i+1
def Perdict(self,dataArr, labelArr):
m,n = np.shape(dataArr)
HideB = np.ones((1,m)) #相当于隐藏层增加一个B
hide_input= np.dot(self.V, dataArr.T) #隐藏层输入NetJ 公式2
hide_output = self.Sigmoid(hide_input) #隐藏层输出 公式 3
self.Y = np.vstack((hide_output,HideB )) ##行顺序添加一个数组,增加一个参数B, 变成下一层的输入 公式4
out_input = np.dot(self.W, self.Y) #输出层输入, 公式5
perdictY = self.Sigmoid(out_input)#输出层输出,公式6
#(2,307)
#print("\n perdictY: \n ",perdictY)
Y= perdictY[0,:]
errNum = 0
for i in range(m):
label = int(labelArr[i]+0.5) ##标签值
out = int(Y[i]+0.5) ##预测值
if label !=out:
errNum +=1
#print("\n i",i ,"\t Y: ",label, "\t predict: ",out)
err = float(errNum/m)*100
print("\n 测试样本总数:",m,"\t 错误率 :%f "%err,"\t 错误样本 ",errNum)
bpNet = BP()
#bpNet.LoadData("data.txt")
bpNet.LoadCancerData()
bpNet.Train()
print("\n ====开始测试了==== \n ")
bpNet.Perdict(bpNet.testData, bpNet.testLabel)
参考文档





















