一、模糊控制基本概念
1. 定义
以模糊集合理论、模糊语言变量及模糊推理为基础的一类控制方法。模糊控制原理框图如图1-1所示。

图1-1 模糊控制原理框图
注:图片来源于《智能控制》(第4版),刘金坤
2. 组成
模糊控制器(Fuzzy Controller ,FC)也称为模糊逻辑控制器(Fuzzy Logic Controller ,FLC),整个控制器包括:模糊化接口、知识库、推理机、解模糊接口。

图1-2 模糊控制器组成框图
注:图片来源于《智能控制》(第4版),刘金坤。
二、模糊控制特点
(1)模糊控制不需要被控对象的数学模型;
(2)模糊控制是一种反映人类智慧的智能控制方法;
(3)构造容易,鲁棒性和适应性好。
三、模糊控制器设计—以洗衣机的模糊控制为例
模糊控制器最简单的实现方法是将一系列模糊控制规则离线转化为一个查询表(又称为控制表) ,存储在计算机中供在线控制时使用。这种模糊控制器结构简单,使用方便,是最基本的一种形式。
步骤1:确定模糊控制器结构
选用两输入单输出模糊控制器。控制器的输入为衣物的污泥和油脂,输出为洗涤时间。
步骤2:定义输入、输出模糊集
将污泥分为3 个模糊集:SD(污泥少), MD(污泥中), LD(污泥多);将油脂分为3 个模糊集:NG(油脂少), MG(油脂中), LG(油脂多);将洗涤时间分为5 个模糊集:VS(很短),S(短), M (中等),L(长), VL(很长)。
步骤3:定义隶属度
(1)选用如下三角形隶属函数可实现污泥的模糊化。
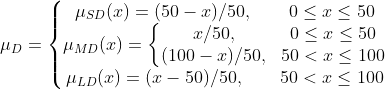
实现代码如下:
clear all;
close all;
N=2;
x=0:0.1:100;
for i=1:N+1
f(i)=100/N*(i-1);
end
u=trimf(x,[f(1),f(1),f(2)]);
figure(1);
plot(x,u);
for j=2:N
u=trimf(x,[f(j-1),f(j),f(j+1)]);
hold on;
plot(x,u);
end
u=trimf(x,[f(N),f(N+1),f(N+1)]);
hold on;
plot(x,u);
xlabel('x');
ylabel('Degree of membership');

图3-1 污泥的隶属度函数
(2)同理,选用如下三角形隶属函数可实现油脂的模糊化。
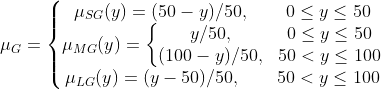

图3-2 油脂的隶属度函数
(3)同理,选用如下三角形隶属函数可实现洗涤时间的模糊化。
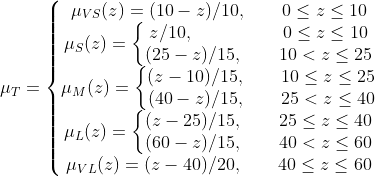

图3-3 洗涤时间的隶属度函数
步骤4:建立模糊规则,并绘制模糊控制表
表3-1 模糊控制表

步骤5:实现模糊推理,分为以下几步
(1)规则匹配
假设
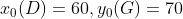
,分别代入所属隶属度函数中,求得隶属度为
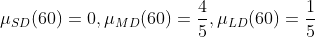
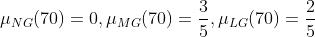
可得到4 条相匹配的模糊规则,如下表
表3-2 模糊推理结果

(2)规则触发
由表3-2可知,被触发的规则有4 条,即

(3)规则前提可信度与规则总可信度
在同一规则内,前提之间通过“与”关系得到规则的结论。前提的可信度之间通过取小运算,由表3-2可得到没一条规则总前提的可信度为

由此得到洗衣机规则前提可信度表,即规则强度表,见表3-3。
表3-3 规则前提可信度

将表3-2和表3-3进行“与运算”,得到每条规则的总可信度,见表3-4所示。
表3-4 规则总可信度

(4)模糊系统总的输出
模糊系统总的可信度为各条规则可信度推理结果的并集,即

可见,有三条规则被触发。
步骤6:解模糊化(以最大隶属度平均法为例)
由表3-4及总的可信度输出结果可知,洗涤时间的隶属度最大值为
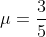
。

图3-4 洗衣机的3个规则被触发
将
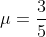
带入洗涤时间的隶属度函数中,得
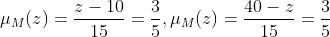
得到
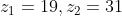

图3-4 洗衣机的组合输出及解模糊化
采用最大平均法,可得精确输出为
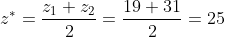
源代码:
%Fuzzy Control for washer
clear all;
close all;
clc
a=newfis('fuzz_wash');
%% 输入变量和输出变量模糊化
a=addvar(a,'input','x',[0,100]); %Fuzzy Stain
a=addmf(a,'input',1,'SD','trimf',[0,0,50]);
a=addmf(a,'input',1,'MD','trimf',[0,50,100]);
a=addmf(a,'input',1,'LD','trimf',[50,100,100]);
a=addvar(a,'input','y',[0,100]); %Fuzzy Axunge
a=addmf(a,'input',2,'NG','trimf',[0,0,50]);
a=addmf(a,'input',2,'MG','trimf',[0,50,100]);
a=addmf(a,'input',2,'LG','trimf',[50,100,100]);
a=addvar(a,'output','z',[0,60]); %Fuzzy Time
a=addmf(a,'output',1,'VS','trimf',[0,0,10]);
a=addmf(a,'output',1,'S','trimf',[0,10,25]);
a=addmf(a,'output',1,'M','trimf',[10,25,40]);
a=addmf(a,'output',1,'L','trimf',[25,40,60]);
a=addmf(a,'output',1,'VL','trimf',[40,60,60]);
%% 建立模糊规则表
rulelist=[1 1 1 1 1; %Edit rule base
1 2 3 1 1;
1 3 4 1 1;
2 1 2 1 1;
2 2 3 1 1;
2 3 4 1 1;
3 1 3 1 1;
3 2 4 1 1;
3 3 5 1 1];
a=addrule(a,rulelist);
showrule(a) %Show fuzzy rule base
%% 解模糊,采用平均最大隶属度法
a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy
%% 读写模糊控制器
writefis(a1,'wash'); %Save to fuzzy file "wash.fis"
a2=readfis('wash');
figure(1);
plotfis(a2);
figure(2);
plotmf(a,'input',1);
figure(3);
plotmf(a,'input',2);
figure(4);
plotmf(a,'output',1);
ruleview('wash'); %Dynamic Simulation
%% 利用模糊控制器求解
x=60;
y=70;
z=evalfis([x,y],a2) %Using fuzzy inference运行结果:

注释:程序中规则表为什么是3行5列的,具体解释如下:
























