RSA 公钥和密钥存redis还是代码里面 rsa公钥密码算法的原理

RSA算法原理简析

 

     当今的信息时代，信息安全显得尤为重要，加密也理所当然成为不可或缺的一部分。所有的加密算法不外乎2种模式：对称加密算法以及非对称加密算法。

     对称加密算法加密解密使用同一种规则，一个致命的缺点就是保存和传递密钥；非对称加密算法加密解密使用不同的规则，公钥加密的信息只有私钥才能解密，只要私钥不泄露，通信就是安全的。RSA是目前最有影响力的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。

 

 

一、介绍

    RSA公钥加密算法是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。RSA取三人姓氏首字母。

    算法基于下面的两个事实,这些事实保证了RSA算法的安全有效性：

      1) 已有确定一个数是不是质数的快速算法；

      2) 尚未找到确定一个合数的质因子的快速算法。

    今天只有短的RSA钥匙才可能被强力方式解破。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。

 

二、数论知识

    进入正题之前，我先介绍一些基本的数论知识，归根到底其实算法就是数学。

 

1、互质关系

        如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

        关于互质关系，不难得到以下结论：

          1)任意两个质数构成互质关系，比如13和61。

          2) 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。

          3) 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。

          4) 1和任意一个自然数是都是互质关系，比如1和99。

          5) p是大于1的整数，则p和p-1构成互质关系，比如57和56。

          6) p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

 

2、欧拉函数

        任意给定正整数n，在小于等于n的正整数之中，与n构成互质关系的有φ(n)个，φ(n)就叫做欧拉函数。

        可以证明， 如果n是质数，则 φ(n)=n-1 。

        一般性地，任意一个大于1的正整数，都可以写成一系列质数的积：

 

       

        那么，

       

 

3、欧拉定理

        如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

       

 

 

        也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。
 

4、费马小定理

        假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

       

 

5、模反元素

        如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。

       

 

        这时，b就叫做a的"模反元素"。        欧拉定理可以用来证明模反元素必然存在：

       

 

        可以看到，a的 φ(n)-1 次方，就是a的模反元素。

 

三、RSA算法密钥生成

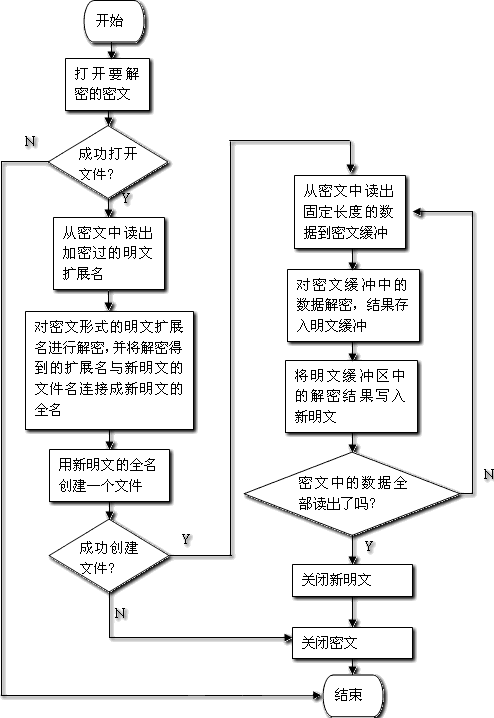
    1、随机选择2个不相等的质数p和q

        例如：61和53。

 

    2、计算p和q的乘积 n=p×q

        n = 61×53 = 3233

        n的长度即为密钥长度，3233写成二进制为110010100001，则密钥长度为12位。

 

    3、计算n的欧拉函数 φ(n) = (p-1)(q-1)

        φ(3233) = 60×52  = 3120

 

    4、随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质

        这里在1到3120之间，随机选择17。（实际应用中，常常选择65537）

 

    5、计算e对于φ(n)的模反元素d

        ed ≡ 1 (mod φ(n)) 

        即 17d ≡ 1 (mod 3720)

        解得其中一个解为d=2753。

 

    6、将n和e封装成公钥，n和d封装成私钥

        n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

        实际应用中，公钥和私钥的数据都采用ASN.1格式表达

 

四、RSA算法加密

公钥(n,e) 只能加密小于n的整数m，如果要加密大于n的整数，有两种解决方法：一种是把长信息分割成若干段短消息，每段分别加密；另一种是先选择一种"对称性加密算法"（比如DES），用这种算法的密钥加密信息，再用RSA公钥加密DES密钥。

 

    加密要用公钥(n,e)，例如要加密信息m（m必须是整数字符串可以取ascii值或unicode值，且m<n），加密就是要算出下面的c

      m^e ≡ c (mod n)

 

    公钥是 (3233, 17)，m假设是65，因为

       65¹⁷ ≡ 2790 (mod 3233)

    于是，c = 2790。

 

五、RSA算法解密

    解密要用私钥(n,d)，可以证明，下面的等式一定成立：

      c^d ≡ m (mod n)

 

    私钥是(3233, 2753)，c等于2790，因为

      2790²⁷⁵³ ≡ 65 (mod 3233)

    于是，m = 65，即加密之前的原数据为65。

 

六、程序实现流程图

    1、密钥生成

 

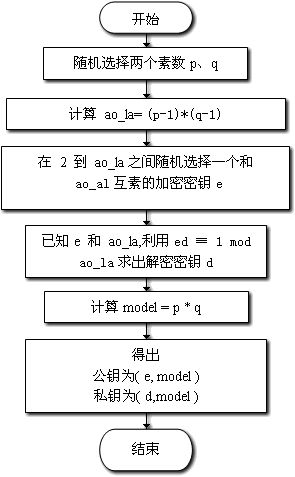
    2、加密

 

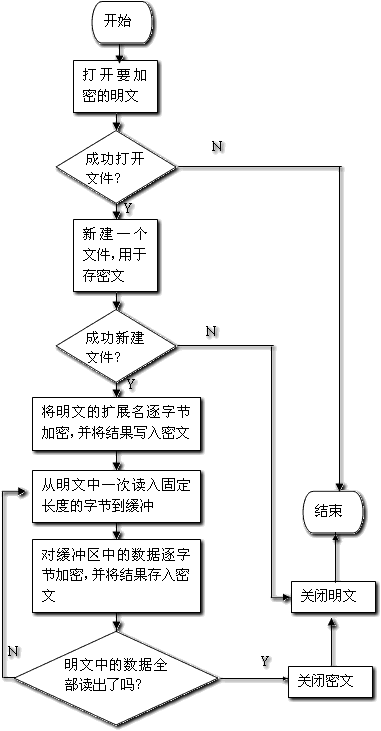
   3、 解密