java经典编程题 java类编程题

转载

mob64ca14010a69 2023-09-04 13:01:55

文章标签 java经典编程题打印菱形星星分子数列累加阶乘累加和 java编程 文章分类 Java 后端开发

一、描述

题目1：
打印出如下菱形图案（菱形）
*
***
*****
*******
*****
***
*
程序分析：先把图形分成两部分来看待，前四行一个规律，后三行一个规律，利用双重 for循环，外层控制行，内层控制列。
对该题进行扩展：由用户输入上半部分的行数，根据行数产生任意行的菱形，如图为用户输入数字5时的结果

*
***
*****
*******
*********
*******
*****
***
*
我们采用两种方法来实现，一种是分上半部分和下半部分分别打印，一个是直接通过条件判断，整个一起打印。

题目2：有一分数序列：2/1，3/2，5/3，8/5，13/8，21/13...求出这个数列的前20项之和。

程序分析：请抓住分子与分母的变化规律,分子从第三项开始，都是前一项分子和分母之和；分母=前一项的分子。
在前面多加1/1项，不计算进该数列，找出项之间的关系；后项分母=前项分子；后项分子=前项分子+前项分母

题目3：求1+2!+3!+...+20!的累加和。

二、源代码

程序1：

<span style="font-size:14px;">package tong.yue.day2;


import java.util.Scanner;


/**
 * 打印出如下图案（菱形）
    *
   *** 
  ***** 
 ******* 
  ***** 
   *** 
    * 
程序分析：先把图形分成两部分来看待，前四行一个规律，后三行一个规律，利用双重 for循环，外层控制行，内层控制列。
对该题进行扩展：由用户输入上半部分的行数，根据行数产生任意行的菱形，如图为用户输入数字5时的结果


     *
    ***
   *****
  *******
 *********
  *******
   *****
    ***
     *
我们采用两种方法来实现，一种是分上半部分和下半部分分别打印，一个是直接通过条件判断，整个一起打印。
 * @author tong
 *
 */


public class PrintDiamond {


	public static void main(String[] args) {
		
		Scanner scanner = new Scanner(System.in);
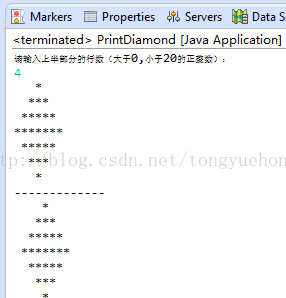
		System.out.println("请输入上半部分的行数（大于0,小于20的正整数）：");
		int line = scanner.nextInt();
		if (line<=0||line>20) {
			System.out.println("输入数据有误，请重新输入上半部分的行数（大于0,小于20的正整数）：");
			line = scanner.nextInt();
		}		
		printDiamondByOneFor(line);
		System.out.println("-------------");
		printDiamondByTwoFor(line);
		
	}
	
	 //打印菱形
	private static void printDiamondByOneFor(int n){
		//根据图形找关系，输入的是上半部分的行数，而打印的"*"与行数满足（2*行号-1）的关系；
		//该图形中间最大的"*"数与输入的上半部分行数的关系为（2*n-1）
		//而两倍的空格数加上"*"号个数为中间最大行行数。
		for (int i = 1; i <= 2*n-1; i++) {
			//打印上半部分
			if (i<=n) {
				//空格数的两倍=中间最大的"*"数-当前行"*"个数
				for (int j = 1; j <= ((2*n-1)-(2*i-1))/2; j++) {
					System.out.print(" ");
				}
				//当前行打印出的"*"
				for (int j = 1; j <= 2*i-1; j++) {
					System.out.print("*");
				}
			//打印下半部分
			}else {
				//打印的空格数=当前行号-输入的上半部分行数
				for (int j = 1; j <= i-n; j++) {
					System.out.print(" ");
				}
				//"*"数=中间最大的"*"数-当前行空格个数*2
				for (int j = (2*n-1)-2*(i-n); j >=1 ; j--) {
					System.out.print("*");
				}
			}
			System.out.println();
		}
	}
	
	  //打印菱形
	private static void printDiamondByTwoFor(int n){
		//打印上半部分
		for(int i=0;i<n;i++){
			for(int j=0;j<2*n;j++){
		  	if(j<n-i){
		  	  System.out.print(" ");
		  	}else {
		  		if(j<=n+i){
				  	  System.out.print("*");
		  		}
			}
		  	
		  }
		  System.out.println();
		}
		//打印下半部分
		for(int i=1;i<n;i++){
			System.out.print(" ");
			for(int j=0;j<2*n-i;j++){
				if(j<i){
					System.out.print(" ");
				}else {
					if(j<2*n-i-1){
					  	  System.out.print("*");
					}
				}
			}	  	  
		  	
			System.out.println();
		}
	}


}
</span>

运行结果：

java经典编程题 java类编程题_分子数列累加

程序2：

<span style="font-size:14px;">package tong.yue.day2;


import java.util.Scanner;


/**
 * 有一分数序列：2/1，3/2，5/3，8/5，13/8，21/13...求出这个数列的前20项之和。
         程序分析：请抓住分子与分母的变化规律,分子从第三项开始，都是前一项分子和分母之和；分母=前一项的分子。
         在前面多加1/1项，不计算进该数列，找出项之间的关系
         后项分母=前项分子
         后项分子=前项分子+前项分母
 * @author tong
 *
 */


public class Fraction {


	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		System.out.println("请输入加和的项数(<=50)：");
		int line = scanner.nextInt();
		if (line<=0||line>50) {
			System.out.println("输入数据有误，请重新输入加和的项数(<=50)：");
			line = scanner.nextInt();
		}			
		printSum(line);
	}


	private static void printSum(int line) {
				
		double denominator = 1;//分母
		double  molecular = 1;//分子
		double fraction  = molecular/denominator;
		double sum = 0;
		//1/1,2/1，3/2，5/3，8/5，13/8，21/13
		//在前面多加1/1项，不计算进该数列，找出项之间的关系
		//后项分母=前项分子
		//后项分子=前项分子+前项分母		
		for (int i = 1; i <= line; i++) {			
			double d = molecular;
			double m = denominator;
			molecular = d+m;//后项分子=前项分子+前项分母
			denominator = d;//后项分母=前项分子
			sum +=molecular/denominator;  //求和
			System.out.println("第"+i+"项："+molecular+"/"+denominator);
		}
		
		System.out.println("前"+line+"项的和为："+sum);
				
	}


}</span>

运行结果：

java经典编程题 java类编程题_java编程_02

程序3：

<span style="font-size:14px;">package tong.yue.day2;


import java.util.Scanner;


/**
 * 求1+2!+3!+...+20!的和,本题目要求阶乘累加和。
 * @author tong
 *
 */


public class FactorialSum {


	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		System.out.println("请输入阶乘加和的项数(<=20)：");
		int line = scanner.nextInt();
		if (line<=0||line>20) {
			System.out.println("输入数据有误，请重新输入阶乘加和的项数(<=20)：");
			line = scanner.nextInt();
		}			
		printFactorialSum(line);


	}


	private static void printFactorialSum(int line) {
		long sum = 0; //累加变量
		long temp = 1;	//累乘变量	
		for (int i = 1; i <= line ; i++) {
			//根据项数循环，从1！+2！+...+line!
			for (int j = 1; j <= i; j++) {
				temp *= j;				
			}
			sum += temp;
			//每次累加一次，该变量恢复为1，继续下次累加
			temp = 1;
		}
		
		System.out.println("该阶乘的累加或为："+sum);
		
	}


}</span>

运行结果：

java经典编程题 java类编程题_java经典编程题_03