Deep Learning 近年来在各个领域都取得了 state-of-the-art 的效果,对于原始未加工且单独不可解释的特征尤为有效,传统的方法依赖手工选取特征,而 Neural Network 可以进行学习,通过层次结构学习到更利于任务的特征。得益于近年来互联网充足的数据,计算机硬件的发展以及大规模并行化的普及。本文主要简单回顾一下 MLP ,也即为Full-connection Neural Network ,网络结构如下,分为输入,隐层与输出层,除了输入层外,其余的每层激活函数均采用 sigmod ,MLP 容易受到局部极小值与梯度弥散的困扰,如下图所示:

MLP 的 Forward Pass
MLP 的 BP 算法基于经典的链式求导法则,首先看前向传导,对于输入层有 I 个单元, 对于输入样本 (x,z) ,隐层的输入为:
ah=∑i=1Iwihxi
bh=f(ah)
这里函数
f为 非线性激活函数,常见的有sigmod或者是
tanh,本文选取
sigmod作为激活函数。计算完输入层向第一个隐层的传导后,剩下的隐层计算方式类似,用
hl表示第
l层的单元数:
ah=∑h′=1hl−1wh′hbh′
bh=f(ah)
对于输出层,若采用二分类即
logisticregression,则前向传导到输出层:
a=∑h′wh′hbh′
y=f(a)
这里
y即为MLP的输出类别为
1的概率,输出类别为0的概率为
1−y,为了训练网络,当
z=1时,
y越大越好,而当z=0时,
1−y越大越好,这样才能得到最优的参数
w,采用MLE的方法,写到一起可以得到
yz(1−y)1−z这便是单个样本的似然函数,对于所有样本可以列出
log似然函数
O=∑(x,z)zlogy+(1−z)log(1−y),直接极大化该似然函数即可,等价于极小化以下的
−log损失函数:
O=−⎡⎣∑(x,z)zlogy+(1−z)log(1−y)⎤⎦
对于多分类问题,即输出层采用
softmax,假设有
K个类别,则输出层的第k个单元计算过程如下:
ak=∑h′wh′kbh′
yk=f(ak)
则得到类别
k的概率可以写作∏kyzkk,注意标签
z中只有第k维为
1,其余为0,所以现在只需极大化该似然函数即可:
O=∏(x,z)∏kyzkk
同理等价于极小化以下损失:
O=−∏(x,z)∏kyzkk
以上便是
softmax的损失函数,这里需要注意的是以上优化目标
O均没带正则项,而且logistic与
softmax最后得到的损失函数均可以称作交叉熵损失,注意和平方损失的区别。
Backward Pass
有了以上前向传导的过程,接下来看误差的反向传递,对于sigmod来说,最后一层的计算如下:a=∑hwh⋅bh , y=f(a)=σ(a)这里bh为倒数第二层单元h的输出,σ为sigmod激活函数,且满足σ′(a)=σ(a)(1−σ(a)),对于单个样本的损失 :
O=−[zlog(σ(a)+(1−z)log(1−σ(a))]
可得到如下的链式求导过程:
∂O∂wh=∂O∂a⋅∂a∂wh
显而易见对于后半部分
∂a∂wh为
bh,对于前半部分
∂O∂a:
∂O∂a=−∂[z log(σ(a))+(1−z)log(1−σ(a))]∂a=−[zσ(a)−1−z1−σ(a)]σ′(a)=−[zσ(a)−1−z1−σ(a)]σ(a)(1−σ(a))=σ(a)−z=y−z
以上,便得到了
logistic的残差,接下来残差反向传递即可,残差传递形式同
softmax,所以先推倒
softmax的残差项,对于单个样本,
softmax的
log损失函数为:
O=−∑izilogyi
其中:
yi=eai∑jeaj
根据以上分析,可以得到
yk′关于
ak的导数:
∂yk′∂ak=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∑i≠keaj⋅eak∑jeaj⋅∑jeajeak′⋅eak∑jeaj⋅∑jeaj=yk(1−yk) k′=k=−yk′yk k≠k
现在能得到损失函数
O对于ak的导数:
∂O∂ak=∂[−∑izilogyi]∂ak=−∑izi⋅∂logyi∂ak=−∑izi1yi∂yi∂ak=−zk(1−yk)−∑i≠kzi1yi(−yiyk)=−zk+zkyk+∑i≠kziyk=−zk+yk(∑izi)=yk−zk
这里有
∑izi=1,即只有一个类别。 到这一步,
softmax 与
sigmod 的残差均计算完成,可以用符号
δ 来表示,对于单元 j ,其形式如下:
δj=∂O∂aj
这里可以得到
softmax 层向倒数第二层的残差反向传递公式:
δh=∂O∂bh⋅∂bh∂ah=∂bh∂ah∑k∂O∂ak⋅∂ak∂bh=f′(ah)∑kwhkδk
其中
ak=∑hwhkbh,对于
sigmod 层,向倒数第二层的反向传递公式为:
δh=∂O∂bh⋅∂bh∂ah=∂bh∂ah⋅∂O∂a⋅∂a∂bh=f′(ah)whδ
以上公式的
δ 代表 sigmod 层唯一的残差,接下来就是残差从隐层向前传递的传递过程,一直传递到首个隐藏层即第二层(
注意,残差不会传到输入层,因为不需要,对输入层到第二层的参数求导,其只依赖于第二层的残差,因为第二层是这些参数的放射函数):
δh=f′(ah)∑h′=1hl+1whh′δh′
整个过程可以看下图:
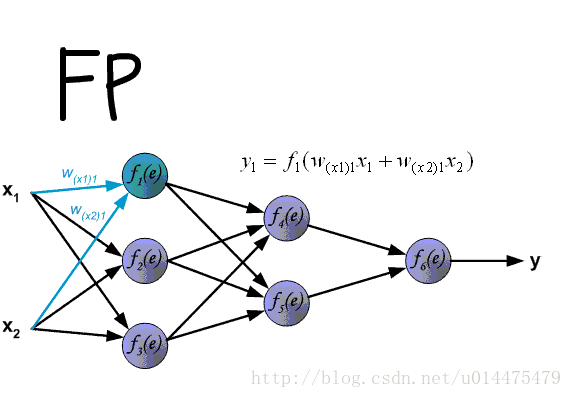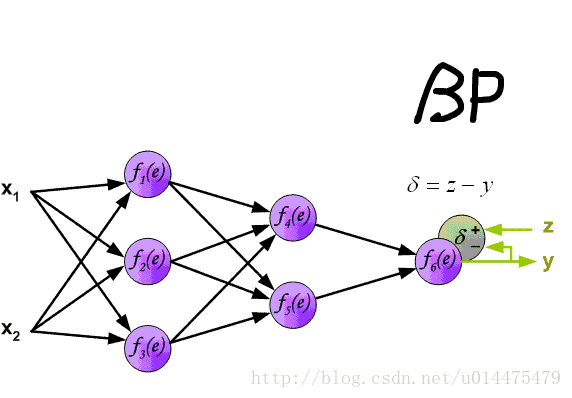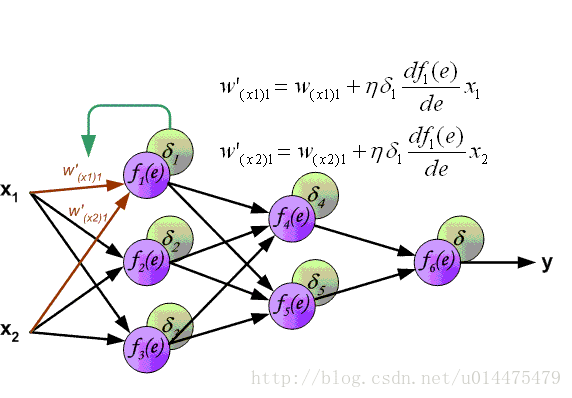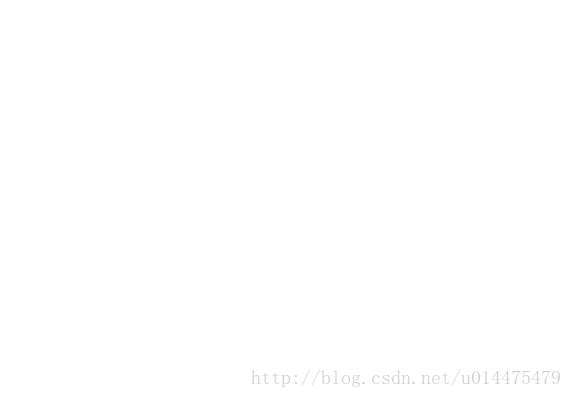
最终得到关于权重的计算公式:
∂O∂wij=∂O∂aj∂aj∂wij=δjbi
至此完成了
backwark pass 的过程,注意由于计算比较复杂,有必要进行梯度验证。对函数
O 关于参数 wij 进行数值求导即可,求导之后与与上边的公式验证差异,小于给定的阈值即认为我们的运算是正确的。





















