标准差
标准差(又称标准偏差、均方差,英语:Standard Deviation,缩写SD),数学符号σ(sigma),在概率统计中最常使用作为测量一组数值的离散程度之用。
标准差定义:
为方差开算术平方根,反映组内个体间的离散程度;标准差与期望值之比为标准离差率。测量到分布程度的结果,原则上具有两种性质:
1、为非负数值(因为开平方后再做平方根);
2、与测量资料具有相同单位(这样才能比对)。
计算公式
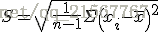
标准误
标准误差(英文:Standard Error),也称标准误,即样本统计量的标准差(英文:Standard Deviation),是描述对应的样本统计量抽样分布的离散程度及衡量对应样本统计量抽样误差大小的尺度。
如果已知数据来源的标准差(σ),那么抽取无限多份大小为 n 的样本,每个样本各有一个平均值,所有这个大小的样本之平均值的标准差可证明为:
Sx¯=σn√ S x ¯ = σ n
但由于通常σ为未知,此时可以用研究中取得样本的标准差 (s) 来估计 SDx¯
S
D
x
¯
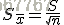
CV值
在概率论和统计学中,变异系数,又称“离散系数”(英文:coefficient of variation),是概率分布离散程度的一个归一化量度,其定义为标准差 σ σ 与平均值 μ μ
Cv=σμ C v = σ μ
变异系数(coefficient of variation)只在平均值不为零时有定义,而且一般适用于平均值大于零的情况。变异系数也被称为标准离差率或单位风险。
变异系数只对由比率标量计算出来的数值有意义。举例来说,对于一个气温的分布,使用开尔文或摄氏度来计算的话并不会改变标准差的值,但是温度的平均值会改变,因此使用不同的温标的话得出的变异系数是不同的。也就是说,使用区间标量得到的变异系数是没有意义的。





















