一、描述
1、将一个正整数分解质因数。例如:输入90,打印出90=2*3*3*5。
程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,输出之前的所有因子。
(2)如果n!=k,但n能被k整除,则应打印出k的值,并用n除以k的商作为新的正整数n,重复执行第一步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
2、利用条件运算符的嵌套来完成此题:学习成绩>=90分的同学用A表示,60-89分之间的用B表示,60分以下的用C表示。
程序分析:(a>b)?a:b这是条件运算符的基本例子。
3、输入两个正整数m和n,求其最大公约数和最小公倍数。
二、源代码
1、程序1
package tong.yue.hong;
import java.util.Scanner;
/*
* 题目:将一个正整数分解质因数。例如:输入90,打印出90=2*3*3*5。
程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,打印出即可。
(2)如果n<>k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n,重复执行第一步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
*/
public class Zhiyinshu {
public static void main(String[] args) {
System.out.println("Please input a number bigger than one:");
Scanner scan = new Scanner(System.in);
int num = scan.nextInt();
while (num<=1) {
System.out.println("input number error,please input again!");
num = scan.nextInt();
}
decompose(num);
decompose2(num);
}
/**
* 使用字符串的拼接
* @param n
*/
private static void decompose(int n){
System.out.print(n+"=");
for(int i=2;i<=n;i++){
while(n%i==0 && n!=i){
n/=i;
System.out.print(i+"*");
}
if(n==i){
System.out.println(i);
break;
}
}
}
/**
* StringBuilder将输出结果格式化
* @param num
*/
private static void decompose2(int num){
StringBuilder sBuilder = new StringBuilder();
sBuilder.append(num+"=");
int i = 2;
while(num!=1){
if(num%i==0){
sBuilder.append(i+"*");
num /=i;
}else {
i++;
}
}
String resulString=sBuilder.toString();
System.out.println(resulString.substring(0, resulString.length()-1));
}
}运行结果:
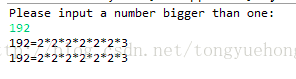
2、程序2
package tong.yue.hong;
import java.util.Scanner;
/**
* 题目:利用条件运算符的嵌套来完成此题:学习成绩>=90分的同学用A表示,60-89分之间的用B表示,60分以下的用C表示。
程序分析:(a>b)?a:b这是条件运算符的基本例子。
* @author Administrator
*
*/
public class GradeLevel {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Please input a score:(0-100)");
int score = scanner.nextInt();
while(score<0||score>100){
System.out.println("Input score error,please input a score again:");
score = scanner.nextInt();
}
//条件运算符的嵌套,如果大于等于90分就输出等级A,否则继续判断是否大于等于60,若是则是B,否则为C
String level = score>=90?"A":score>=60?"B":"C";
System.out.println(score+"分的等级为"+level);
}
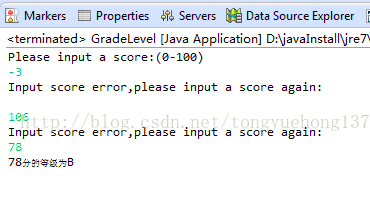
}运行结果:
3、程序3
package tong.yue.hong;
import java.util.Scanner;
/**
* 输入两个正整数m和n,求其最大公约数和最小公倍数。
* @author tong
*
*/
public class CommonDivMulpi {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Please input the first number(num>0):");
int firstNum = scanner.nextInt();
while(firstNum<0){
System.out.println("Input error,Please input the first number again(num>0):");
firstNum = scanner.nextInt();
}
System.out.println("Please input the second number(num>0):");
int secondNum = scanner.nextInt();
while(secondNum<0){
System.out.println("Input error,Please input the second number again(num>0):");
secondNum = scanner.nextInt();
}
//如果两个数相等,则最小公倍数就是其中之一,无需调用方法判断
if (firstNum==secondNum) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+firstNum);
greatCommonDivisor(firstNum,secondNum);
}else {
leastCommonMultiple(firstNum,secondNum);
greatCommonDivisor(firstNum,secondNum);
}
max_min(firstNum,secondNum);
}
/**
* 求最小公倍数:首先获取该两个数的较大者,若两者中的较大者是较小者的倍数,则该较大者则为两数最小公倍数
* 本代码采用列举倍数法:如果两者不成倍数关系,则取较大数的倍数(从2开始一次往上增加),
* 用该数除以较小的数,如果可以整除,该数就是要求者,否则继续取倍数重复以上部分
* 例如:12与20的最小公倍数,20不能整除12,将20*2=40,40不能整除12 ,将20*3=60,此时60可以整除12,所以二者最小公倍数为60
* @param firstNum
* @param secondNum
*/
private static void leastCommonMultiple(int firstNum, int secondNum) {
//判断两者中的较大者
if (firstNum>secondNum) {
if (firstNum%secondNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+firstNum);
}else {
//若两个数互质,那么最坏的情况就是公倍数是两者的乘积
for (int i = 2; i <= secondNum; i++) {
if (firstNum*i%secondNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+firstNum*i);
break;
}
}
}
}else {
if (secondNum%firstNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+secondNum);
}else {
//若两个数互质,那么最坏的情况就是公倍数是两者的乘积
for (int i = 2; i <= firstNum; i++) {
if (secondNum*i%firstNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+secondNum*i);
break;
}
}
}
}
}
/**
* 最大公约数求法:若两数成倍数关系,则较小的那个数就是最大公约数
* 否则,较小数循环除以较小数之的所有因子(从小到大)的结果去循环除较大数,如果能整除,该数就是最大公约数,否则继续循环
* 例如:36和10求最大公约数,36不是10的倍数,则用较小数10的因子去除较小数,除后结果去除36,则用36%(10/2)=36%5无法整除,36%(10/5)=36%2==0整除,所以最大公约数是2
* @param firstNum
* @param secondNum
*/
private static void greatCommonDivisor(int firstNum, int secondNum) {
//判断两者中的较大者
if (firstNum>secondNum) {
if (firstNum%secondNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最大公约数为"+secondNum);
}else {
//若两个数互质,那么最坏的情况就是最大公约数是1
for (int i = 2; i <= secondNum; i++) {
//取出较小数的因子
if (secondNum%i==0&&firstNum%(secondNum/i)==0) {
System.out.println(firstNum+"和"+secondNum+"的最大公约数为"+(secondNum/i));
break;
}
}
}
}else {
if (secondNum%firstNum==0) {
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+firstNum);
}else {
//若两个数互质,那么最坏的情况就是最大公约数是1
for (int i = 2; i <= secondNum; i++) {
//取出较小数的因子
if (firstNum%i==0&&secondNum%(firstNum/i)==0) {
System.out.println(firstNum+"和"+secondNum+"的最大公约数为"+(firstNum/i));
break;
}
}
}
}
}
/**
* 求最大公约数和最小公倍数,使用辗转除法,同时求最大公约数和最小公倍数
* 其中最大公约数是该两个数中所有相同因子的乘积,而最小公倍数则是所有相同的分解因子和各自特有的因子的乘积
* @param m
* @param n
*/
private static void max_min(int firstNum, int secondNum){
int m = firstNum;
int n = secondNum;
int temp = 1;
int yinshu = 1;
int beishu = m*n;
//将两数中的较小者放在前面
if(n<m){
temp = n;
n = m;
m = temp;
}
//使用辗转除法
while(m!=0){
temp = n%m;
n = m;
m = temp;
}
yinshu = n;
beishu /= n;
System.out.println(firstNum+"和"+secondNum+"的最大公约数为"+yinshu);
System.out.println(firstNum+"和"+secondNum+"的最小公倍数为"+beishu);
}
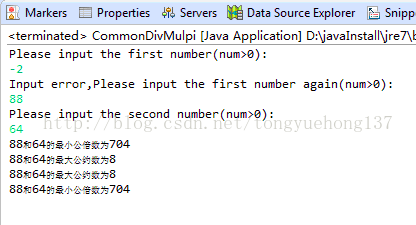
}运行结果: