
繁杂的样本
难以抹去你的光芒
我只希望我
能够一睹你的模样
——题记
这诗让我憋了半个小时才憋出来……
CNN各层通道数的设置
CNN和DNN不同,每层不是一维的,而是三维的,有长宽厚三个维度。输入层(可以当做汇合层与下一卷积层连接)的通道数往往是3,分别保存RGB三色(如果是灰度图,通道数可以设为1,保存的颜色可以是RGB中的任意一个,反正它们都相等)。
对于通道数为n前层,下一层卷积层的通道数为m,那么我们通常取其卷积核数为
——这里的卷积核是二维的矩阵,但如果将卷积核认为是三维的,那么卷积核数则为
,即后层的通道数,此时每个卷积核的“厚度”和上一层相同:

前一层的一块相邻区域,对应卷积层的一个输出
这是的CNN有些像全连接网络,因为它的通道全连接了。当然也可以像LeNet结构一样,指定通道的连接,这时的CNN结构就有些像局部连接的DNN。
网络最后一层和全连接层连接时,连接方法有三种:
- 使用全局卷积核,即将第一层全连接层看作特殊的卷积层,其输出为 。
- 将最后一层 的输出Reshape成一个 的输出,作为全连接层的第一层。
- 使用空间金字塔池化层。关于这个层级结构,我们会在后面介绍。
对于全连接层,没有长宽厚的概念,只有神经元数量来表示层的复杂程度。我们通常也把这个数量认为是通道数。全连接层所有神经元不像卷积层、汇合层神经元一样有位置与顺序的区别。前向传播和反向传播完全可以当做全连接DNN处理。

卷积神经网络的结构示意图
CNN各层的参数
由于激活层和池化层没有参数(只有长宽、通道数、激活函数和层数这几个超参数),CNN的所有需要学习的参数都在卷积层和全连接层。
卷积层的参数就是卷积核的公共权值和每个通道的公共偏置量,超参数就是长宽厚、层数、卷积核数量等等。
CNN的前向传播过程
卷积层
首先,卷积层有多种卷积方式,常见的有五种:Valid、Same、Full、Strided、Fractional_strided,区别在于输出的长宽不同。计算公式如下:
1. Valid卷积,就是前文介绍的舍弃不存在元素的卷积。后层的长
,宽
。
2. Same卷积,无论卷积核多大,输入和输出保持了相同的规模,即长
,宽
。卷积的过程可以看作在输入矩阵的外圈补了若干圈的零,然后进行Valid卷积实现。根据公式可知,其在上下/左右补零的行/列数各为
、
:

卷积核大小为5x5,则上下各补两行“0”,左右也各补两列“0”
3. Full卷积,就是前文介绍的完全补0的卷积。后层的长
,宽
。易知上下/左右补0的行/列数分别等于卷积核的核高和核宽。
4. Strided卷积,即跨步卷积,即卷积核并不是一格一格地滑动,而是隔几行隔几列再卷积一次:

一个步长为2的Strided卷积示意图
后层的长
,宽
。这里的取值,如果是下取整,那么就舍弃输入中不足一步的边缘;有时也会是上取整,表示如果输入中不足一步,则在边缘补0,不“浪费”这些部分。
5. Fractional_strided卷积,即小数步长的跨步卷积,其本质则是在输入矩阵相邻格子之间补0。而外层更是要补0——这个补0方法和Full卷积相同:

Fractional_strided卷积示意图,紫色为原输入,灰色为补0
接下来我们将前层的长宽厚表示为
、
、
,后层的长宽厚表示为
、
、
,那么卷积层的卷积则表示成
。
其中Valid卷积的实现为
。
可以看出,Valid卷积层的卷积的过程如下:
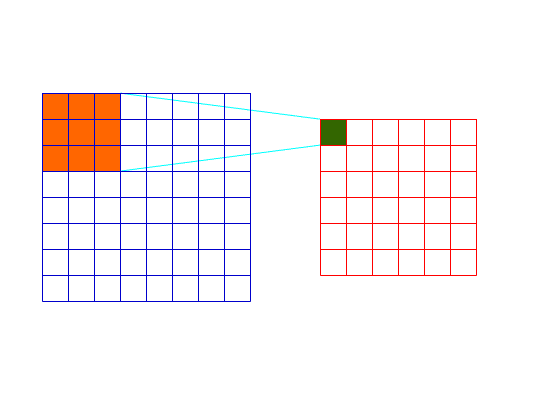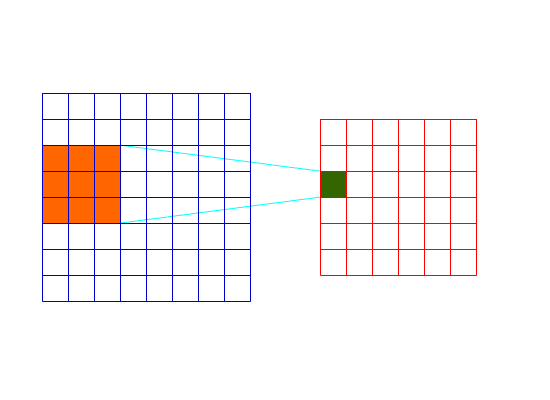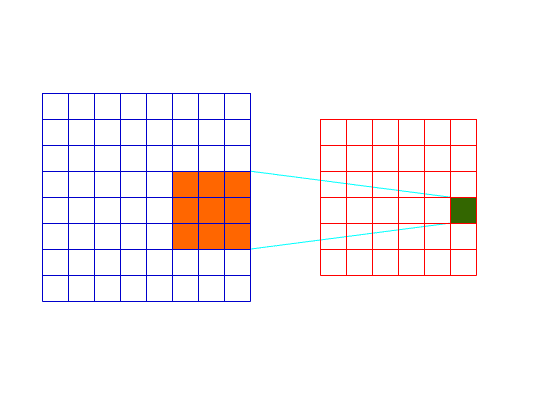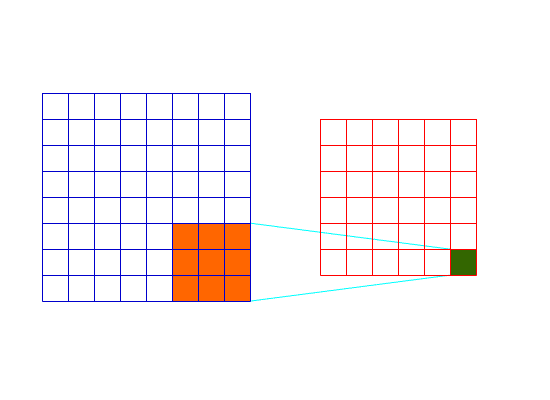
Valid卷积过程1
而Full卷积可以使得图片边缘位置和图片中间位置对下一层的贡献相同:
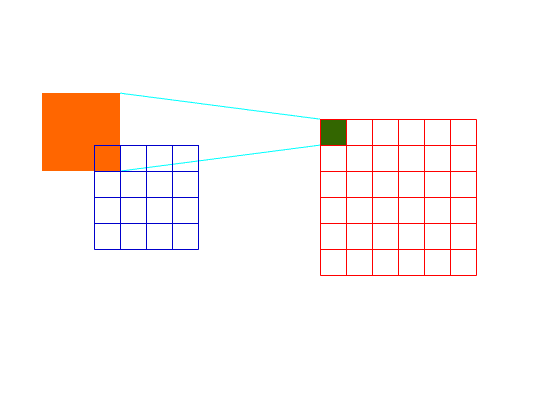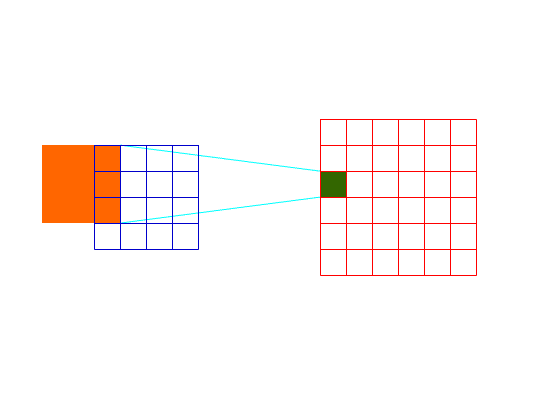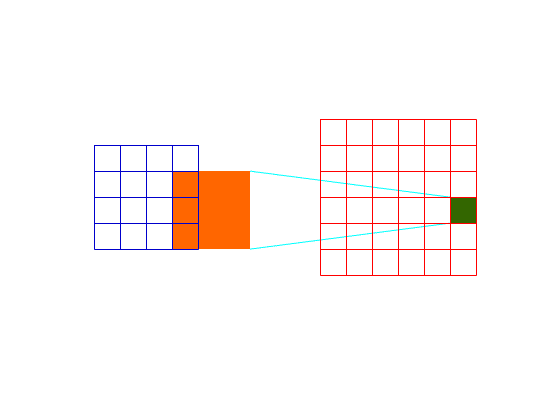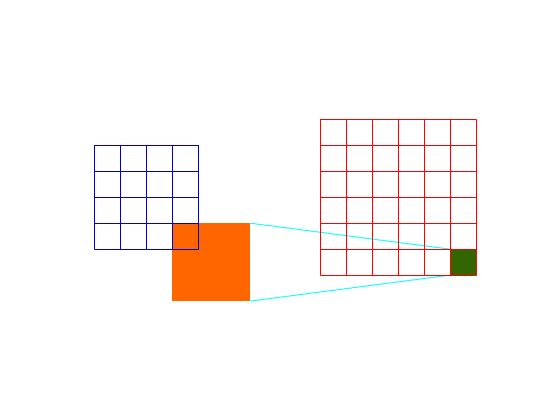
Full卷积过程2
对于这两种卷积,以及其他三种卷积,反向传播过程略有不同,下一篇将会分别介绍。
下一步则是对卷积层的激活:
,或者写成
。
接下来就是汇合操作。首先我们算出池化核大小:
,
。
如果我们使用max_pooling(最大池化),那么:
。其中
。
即我们挑选出上一层池化区域内最大的值,作为汇合层该位置的值;
而如果我们使用average_pooling(均值池化),那么:
。
即我们将上一层池化区域内的值作平均处理,作为汇合层该位置的值。
最后就剩下了全连接层了。用全连接网络的方法,将全连接层信息激活、传递直到输出层。全连接网络的传播有没有忘记呢?这里留一个链接吧~
刘冬煜:五、全连接网络的反向传播算法zhuanlan.zhihu.com






















