在Leetcode刷Single Number这道题的时候,自己的想法就是遍历,想了下别的简便想法,楞是没想出,看了下讨论区的大手的,发现了使用XOR,于是想着补补门阵列了。
Given a non-empty array of integers, every element appears twice except for one. Find that single one.
Example 1:
Input: [2,2,1] Output: 1异或运算符(^)
参加运算的两个数据,按二进制位进行“异或”运算

。
运算规则:0^0=0; 0^1=1; 1^0=1; 1^1=0;即:参加运算的两个对象,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
“异或运算”的特殊作用:
(1)使特定位翻转找一个数,对应X要翻转的各位,该数的对应位为1,其余位为零,此数与X对应位异或即可。
例:X=10101110,使X低4位翻转,用X ^0000 1111 = 1010 0001即可得到。
(2)与0相异或,保留原值 ,X ^ 00000000 = 1010 1110。
其他规律有:
(1)将两数异或的结果与其中一数再进行异或,可以得到另一个数。
例:11^01=10 ; 11^10=01
原理很简单,两数异或的结果保存了两个数上每一个二进制位不同或相同的信息,如果相应的二进制位不同,就标志为1,如果相同,则标志为0。
我们可以利用这个特点交换两个数:
temp=a^b;
a=temp^a;
b=temp^b;
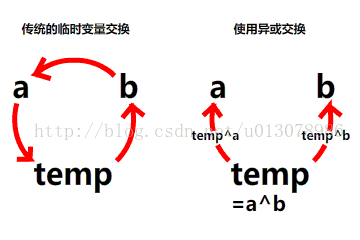
但是使用这种方法似乎与使用临时变量没有什么区别?其实不然,通过简单分析可以发现临时变量的值在整个过程中并没有发生变化,因此也可以无需设置临时变量。
a=a^b^a;
b=a^b^b;
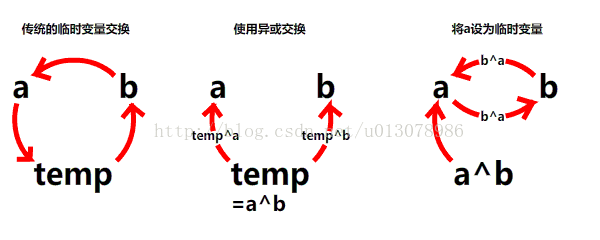
a=a^b;
b=b^a;
a=b^a;还可以写得更简洁一点:
a^=b^=a^=b;还可以通过加减实现两数互换:
a=a+b
b=a-b;
a=a-b;前提是a+b的值不能溢出。
(2)一个数与另一个数异或两次是其本身
8^9^9=8
按位与运算符(&)
参加运算的两个数据,按二进制位进行“与”运算。
运算规则:0&0=0; 0&1=0; 1&0=0; 1&1=1;
即:两位同时为“1”,结果才为“1”,否则为0
例如:3&5 即 0000 0011& 0000 0101 = 00000001 因此,3&5的值得1。
另,负数按补码形式参加按位与运算。
“与运算”的特殊用途:
(1)清零。如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零。
(2)取一个数中指定位
方法:找一个数,对应X要取的位,该数的对应位为1,其余位为零,此数与X进行“与运算”可以得到X中的指定位。
例:设X=10101110,取X的低4位,用 X & 0000 1111 = 00001110 即可得到;
还可用来取X的2、4、6位。
(3)保留指定位
与一个数进行“按位与”运算,此数在该位取1.
例如:有一数84,即01010100,想把其中从左边算起的第3,4,5,7,8位保留下来
01010100
&
00111011
—————
00010000(4) 取余操作
key % M = key & (M-1)
11 % 8 = 3
1011 & 0111 = 0011 = 3
按位或运算符(|)
参加运算的两个对象,按二进制位进行“或”运算。
运算规则:0|0=0; 0|1=1; 1|0=1; 1|1=1;
即 :参加运算的两个对象只要有一个为1,其值为1。
例如:3|5 即 00000011 | 0000 0101 = 00000111 因此,3|5的值得7。
另,负数按补码形式参加按位或运算。
“或运算”特殊作用:
(1)常用来对一个数据的某些位置1。
方法:找到一个数,对应X要置1的位,该数的对应位为1,其余位为零。此数与X相或可使X中的某些位置1。
例:将X=10100000的低4位置1 ,用X | 0000 1111 = 1010 1111即可得到。























