一、排序算法概述
常用的内部排序方法有:交换排序(冒泡排序、快速排序)、选择排序(简单选择排序、堆排序)、插入排序(直接插入排序、希尔排序)、归并排序、基数排序(一关键字、多关键字)。
所需辅助空间最多:归并排序
所需辅助空间最少:堆排序
平均速度最快:快速排序
不稳定:快速排序,希尔排序,堆排序。
选择排序算法的依据:任何排序算法在数据量小的时候基本体现不出来差距。选择依据有 1.数据的规模;2.数据的类型;3.数据已有的顺序。
1.数据的规模: 当数据规模较小时,选择直接插入排序或冒泡排序。
2.数据的类型: 如全部是正整数,那么考虑使用桶排序为最优。
3.数据已有的顺序: 快排是一种不稳定的排序(当然可以改进),对于大部分排好的数据,快排会浪费大量不必要的步骤。
数据量极小,而且已经基本排好序,冒泡是最佳选择。我们说快排好,是指大量随机数据下,快排效果最理想。而不是所有情况。
二、计数排序时空复杂度
平均时间复杂度O(n + k),空间复杂度O(n + k),是一种稳定的排序算法。
**比较和非比较的区别
常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较,才能确定自己的位置。
在冒泡排序之类的排序中,问题规模为n,又因为需要比较n次,所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中,问题规模通过分治法消减为logN次,所以时间复杂度平均O(nlogn)。
比较排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。
计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置。
非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)。
非比较排序时间复杂度低,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
三、计数排序原理
计数排序是一种非基于元素比较的排序算法,而是将待排序数组元素转化为计数数组的索引值,从而间接使待排序数组具有顺序性。计数排序的实现一般有两种形式:基于辅助数组和基于桶排序。
计数排序需要占用大量空间,它仅适用于有明确范围,数据比较集中的情况。比如 [0~100],[10000~19999] 这样的数据。
四、计数排序思路
计数排序的基本思想是:对每一个输入的元素arr[i],确定小于 arr[i] 的元素个数。所以可以直接把 arr[i] 放到它输出数组中的位置上。假设有5个数小于 arr[i],所以 arr[i] 应该放在数组的第6个位置上。
计数排序适用于有明确范围的数组,比如给定一个数组,且知道所有值得范围是[m,n]。这个时候可以使用一个n-m+1长度的数组,待排序的数组就可以散在这个数组上,数组的值就是当前值的个数,再经过一次遍历展开,得到的数组就有序了。
1.找出待排序的数组中最大元素n和最小元素m, 新建一个长度为n-m+1的临时数组C
2.统计数组中每个值为i的元素出现的次数,存入数组C(i的最小值为m,最大值为n),C下标为i-m,值为该数字出现的次数;
3.遍历结束,临时数组就存储了每个值的个数
4.最后将它展开赋值给原数组
五、计数排序举例说明
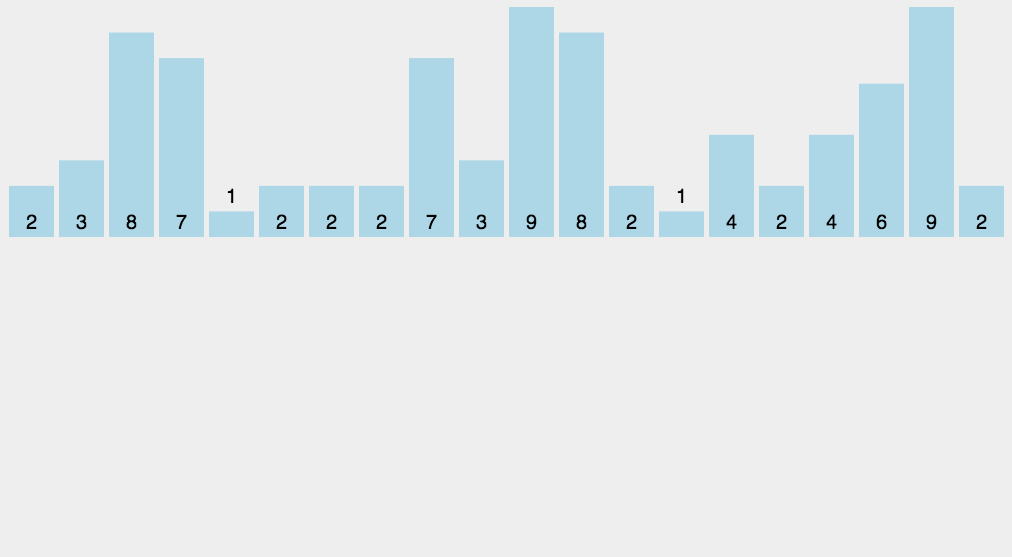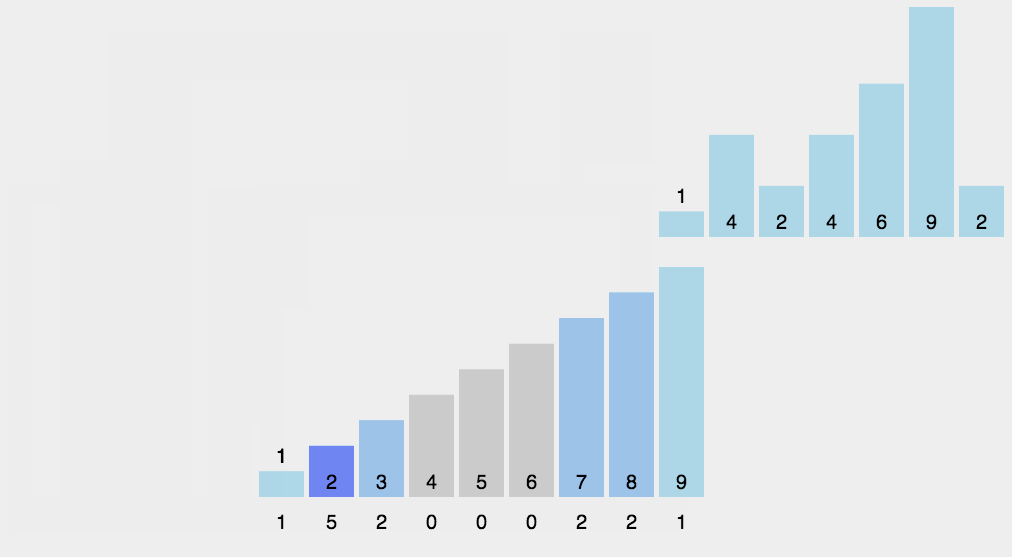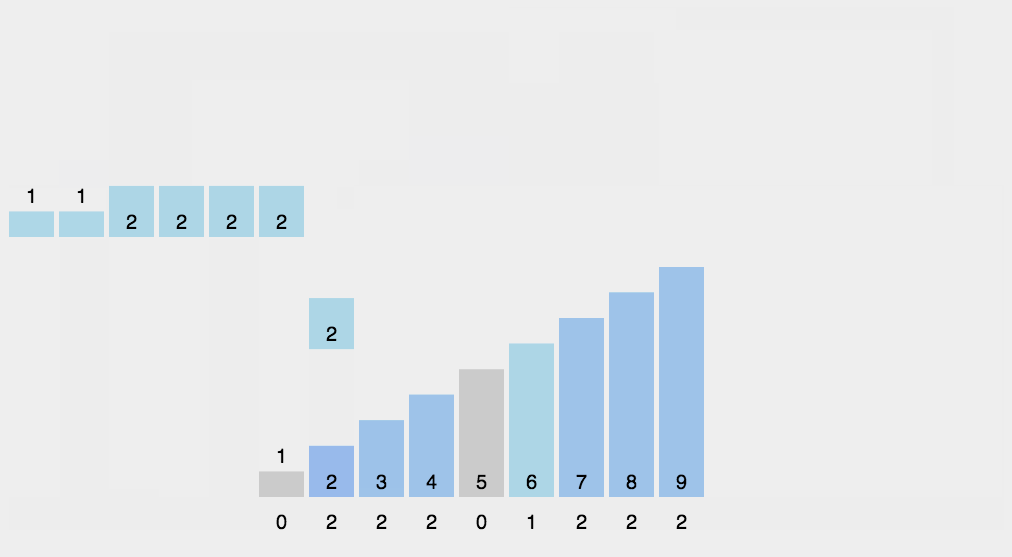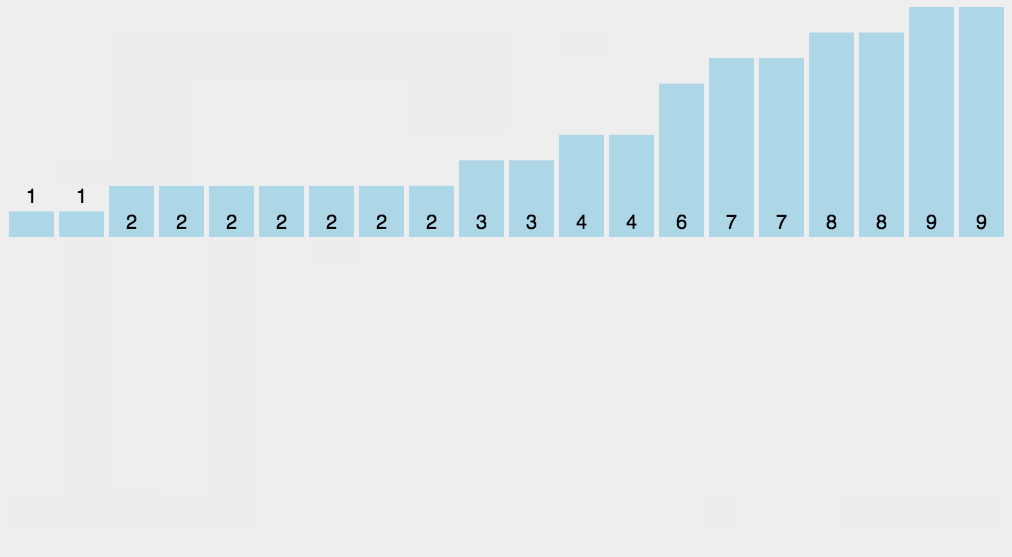
六、计数排序代码
public class CountingSort {
public static void countingSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
// 找出数组中的最大最小值
int bias, min = arr[0], max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
if (arr[i] < min)
min = arr[i];
}
bias = 0 - min;
int[] bucket = new int[max - min + 1];
Arrays.fill(bucket, 0);
// 找出每个数字出现的次数
for (int i = 0; i < arr.length; i++) {
bucket[arr[i] + bias]++;
}
int index = 0, i = 0;
while (index < arr.length) {
if (bucket[i] != 0) {
arr[index] = i - bias;
bucket[i]--;
index++;
} else {
i++;
}
}
}
public static void main(String[] args) {
int[] arrays = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
System.out.println("未排序的数组:" + Arrays.toString(arrays));
countingSort(arrays);
System.out.println("排序后的数组:" + Arrays.toString(arrays));
}
}
// 未排序的数组:[5, 3, 6, 2, 1, 9, 4, 8, 7]
// 排序后的数组:[1, 2, 3, 4, 5, 6, 7, 8, 9]





















