用Python解波动方程 波动方程的数值解

波动方程数值解是波动方程正演、逆时偏移和全波形反演的核心技术之一。本文采用二阶有限差分对波动方程进行了离散，进而实现了对波动方程的数值求解，模拟出其在介质中的传播过程。

1、二维声波波动方程离散

利用泰勒公式进行展开得到：

两式相减得：

则有：

近似得二阶差分算子：

利用二阶中心差分算子对二阶导数进行离散：

将上式代入声波方程得到二阶中心差分格式：

其中：

收敛满足：

其空间和时间差分格式示意图如下图所示：

2、均匀介质二维声波方程求解

初始参数：

# 区域大小
Nx = 301
Nz = 301
# 时间采样数
Nt = 1000
# 速度模型
v = np.ones((Nx+1,Nz+1)) * 3000
u = np.zeros((Nt+1,Nx+1,Nz+1))
h = 5
# 子波主频
fm = 25 
# 空间衰减因子
alpha = 0.5
# 时间步
dt = 1 / Nt
# 空间间隔
dx = h
dy = h
# 迭代公式中的r
A = v **2 * dt ** 2 / h ** 2 
C = v * dt / h

收敛条件判断：

r = np.max(v)*dt/h
assert r < 0.707,f'r should < 0.707, but is {r}'

雷克子波及二维空间衰减函数：

t = np.arange(0, Nt+1)
t0 = 0  # 延迟时间，相当于在t=t0时激发 ，震幅在t0时最大，相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)

x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)

h_x_z =  np.zeros((Nx+1,Nz+1))  #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2))  二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1   # 在Nx//2,Nz//2处激发
h_x_z =  np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2))  # 二维空间衰减函数

x0 = Nx // 2
z0 = Nz // 2
u0 = lambda r, s: 0.25*np.exp(-((r-x0)**2+(s-z0)**2))
JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)

吸收边界条件：
Clayton-Engquist 单成波吸收边界条件:最早是由 Clayton 等人发现并推广的， 其微分表达式为：

其中：n 为边界的外法线方向； s 边界的切线方向。

对上式进行离散得到上、下、左、右边界差分格式如下：

其中：

N 、 M 为边界的网格数。

则有：

# 边界条件
ii = np.arange(Nx+1)
jj = np.arange(Nz+1)
# Clayton-Engquist-majda 二阶吸收边界条件
u[t+1,  0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t,  0, jj] \
                        + 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t,  1, jj] \
                        - C[ 2, jj] ** 2 * u[t,  2, jj] \
                        + (2 * C[ 0, jj] - 1) * u[t - 1,  0, jj] \
                        - 2 * C[ 1, jj] * u[t - 1,  1, jj]


# 下部
u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t,  -1, jj] \
                        + 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t,  -2, jj] \
                        - C[ -3, jj] ** 2 * u[t,  -3, jj] \
                        + (2 * C[ -1, jj] - 1) * u[t - 1,  -1, jj] \
                        - 2 * C[ -2, jj] * u[t - 1,  -2, jj]

# 左部
u[t+1, ii,  0] = (2 - 2 * C[ii,  0] - C[ii,  0] ** 2) * u[t,  ii, 0] \
                        + 2 * C[ii,  1] * (1 + C[ii,  1]) * u[t,  ii, 1] \
                        - C[ii,  2] ** 2 * u[t,  ii, 2] \
                        + (2 * C[ii,  0] - 1) * u[t - 1,  ii, 0] \
                        - 2 * C[ii,  1] * u[t - 1,  ii, 1]
# 右部
u[t+1, ii, -1] = (2 - 2 * C[ii,  -1] - C[ii,  -1] ** 2) * u[t,  ii, -1] \
                        + 2 * C[ii,  -2] * (1 + C[ii,  -2]) * u[t,  ii, -2] \
                        - C[ii,  -3] ** 2 * u[t,  ii, -3] \
                        + (2 * C[ii,  -1] - 1) * u[t - 1,  ii, -1] \
                        - 2 * C[ii,  -2] * u[t - 1,  ii, -2]

Reynolds 边界条件：对于二维声波波动方程，应用二维声波方的微分算子可以 得到：

对上式进行离散可得上下左右边界计算公式：

则有：

#Reynolds 边界条件
u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]

u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]

u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]

u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]

迭代公式：

# 迭代公式
u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]

所有代码如下：

import numpy as np
import imageio.v2 as imageio
import os
import pandas as pd
from matplotlib import pyplot as plt
# 解决中文问题
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False


Nx = 301
Nz = 301
Nt = 1000
v = np.ones((Nx+1,Nz+1)) * 3000
h = 5
fm = 25
alpha = 0.5
dt = 1 / Nt
dx = h
dy = h
A = v **2 * dt ** 2 / h ** 2 
C = v * dt / h

r = np.max(v)*dt/h
assert r < 0.707,f'r should < 0.707, but is {r}'
u = np.zeros((Nt+1,Nx+1,Nz+1))


t = np.arange(0, Nt+1)
t0 = 0  # 延迟时间，相当于在t=t0时激发 ，震幅在t0时最大，相位也在此
s_t = (1 - 2 * (np.pi * fm * dt * (t - t0)) ** 2) * np.exp( - (np.pi * fm * dt * (t - t0)) ** 2)

plt.plot(s_t)
plt.show()

x = np.arange(0,Nx+1)
z = np.arange(0,Nz+1)
x,z = np.meshgrid(x,z)
# print(((z - Nz//2)**2).shape)


h_x_z =  np.zeros((Nx+1,Nz+1))  #np.exp(-0.25 * ((x - Nx//2)**2 + (z - Nz//2)**2))  二维空间衰减函数
h_x_z[Nx//2,Nz//2] = 1   # 在Nx//2,Nz//2处激发
h_x_z =  np.exp(-alpha ** 2 * ((x - Nx//2)**2 + (z - Nz//2)**2))  # 二维空间衰减函数


JJ = np.arange(1,Nz)
II = np.arange(1,Nx)
II,JJ = np.meshgrid(II,JJ)

mode = 'c_e'
img_path = './2_order'
if not os.path.exists(img_path):
    os.makedirs(img_path)

for t in range(2,Nt):
    print('\rstep {} / {}'.format(t ,Nt), end="")
    
    # 边界条件
    ii = np.arange(Nx+1)
    jj = np.arange(Nz+1)
    if mode == 'c_e':
        # Clayton-Engquist-majda 二阶吸收边界条件
        u[t+1,  0, jj] = (2 - 2 * C[ 0, jj] - C[ 0, jj] ** 2) * u[t,  0, jj] \
                                + 2 * C[ 1, jj] * (1 + C[ 1, jj]) * u[t,  1, jj] \
                                - C[ 2, jj] ** 2 * u[t,  2, jj] \
                                + (2 * C[ 0, jj] - 1) * u[t - 1,  0, jj] \
                                - 2 * C[ 1, jj] * u[t - 1,  1, jj]


        # 下部
        u[t+1, -1, jj] = (2 - 2 * C[ -1, jj] - C[ -1, jj] ** 2) * u[t,  -1, jj] \
                                + 2 * C[ -2, jj] * (1 + C[ -2, jj]) * u[t,  -2, jj] \
                                - C[ -3, jj] ** 2 * u[t,  -3, jj] \
                                + (2 * C[ -1, jj] - 1) * u[t - 1,  -1, jj] \
                                - 2 * C[ -2, jj] * u[t - 1,  -2, jj]

        # 左部
        u[t+1, ii,  0] = (2 - 2 * C[ii,  0] - C[ii,  0] ** 2) * u[t,  ii, 0] \
                                + 2 * C[ii,  1] * (1 + C[ii,  1]) * u[t,  ii, 1] \
                                - C[ii,  2] ** 2 * u[t,  ii, 2] \
                                + (2 * C[ii,  0] - 1) * u[t - 1,  ii, 0] \
                                - 2 * C[ii,  1] * u[t - 1,  ii, 1]
        # 右部
        u[t+1, ii, -1] = (2 - 2 * C[ii,  -1] - C[ii,  -1] ** 2) * u[t,  ii, -1] \
                                + 2 * C[ii,  -2] * (1 + C[ii,  -2]) * u[t,  ii, -2] \
                                - C[ii,  -3] ** 2 * u[t,  ii, -3] \
                                + (2 * C[ii,  -1] - 1) * u[t - 1,  ii, -1] \
                                - 2 * C[ii,  -2] * u[t - 1,  ii, -2]
    if mode == 're':
        #Reynolds 边界条件
        u[t+1,ii, 0] = u[t,ii, 0] + u[t,ii, 1] - u[t-1,ii, 1] + C[ii, 1]*u[t,ii, 1] - C[ii, 0]*u[t,ii, 0] -C[ii, 2]*u[t-1,ii, 2] +C[ii, 1]*u[t-1,ii, 1]

        u[t+1,ii,-1] = u[t,ii,-1] + u[t,ii,-2] - u[t-1,ii,-2] + C[ii,-2]*u[t,ii,-2] - C[ii,-1]*u[t,ii,-1] -C[ii,-3]*u[t-1,ii,-3] +C[ii,-2]*u[t-1,ii,-2]

        u[t+1, 0,jj] = u[t, 0,jj] + u[t, 1,jj] - u[t-1, 1,jj] + C[ 1,jj]*u[t, 1,jj] - C[ 0,jj]*u[t, 0,jj] -C[ 2,jj]*u[t-1, 2,jj] +C[ 1,jj]*u[t-1, 1,jj]

        u[t+1,-1,jj] = u[t,-1,jj] + u[t,-2,jj] - u[t-1,-2,jj] + C[-2,jj]*u[t,-2,jj] - C[-1,jj]*u[t,-1,jj] -C[-3,jj]*u[t-1,-3,jj] +C[-1,jj]*u[t-1,-2,jj]


    # 迭代公式
    u[t+1,II,JJ] = s_t[t]*h_x_z[II,JJ]+A[II,JJ]*(u[t,II,JJ+1]+u[t,II,JJ-1]+u[t,II+1,JJ]+u[t,II-1,JJ])+(2-4*A[II,JJ])*u[t,II,JJ]-u[t-1,II,JJ]


    
    plt.imshow(u[t], cmap='gray_r') # 'seismic' gray_r
    # plt.axis('off')  # 隐藏坐标轴
    plt.colorbar()
    if t % 10 == 0:
        plt.savefig(os.path.join(img_path, str(t) + '.png'),
                    bbox_inches="tight", # 去除坐标轴占用空间
                    pad_inches=0.0) # 去除所有白边
        plt.pause(0.05)
        
    plt.cla()
    plt.clf()  # 清除所有轴，但是窗口打开，这样它可以被重复使用
plt.close()

# 保存gif
filenames=[]
for files in os.listdir(img_path ):
    if files.endswith('jpg') or files.endswith('jpeg') or files.endswith('png'):
        file=os.path.join(img_path ,files)
        filenames.append(file)

images = []
for filename in filenames:
    images.append(imageio.imread(filename))

imageio.mimsave(os.path.join(img_path,  'wave.gif'), images,duration=0.0001)

最终得到有边界为0、吸收条件结果如下：

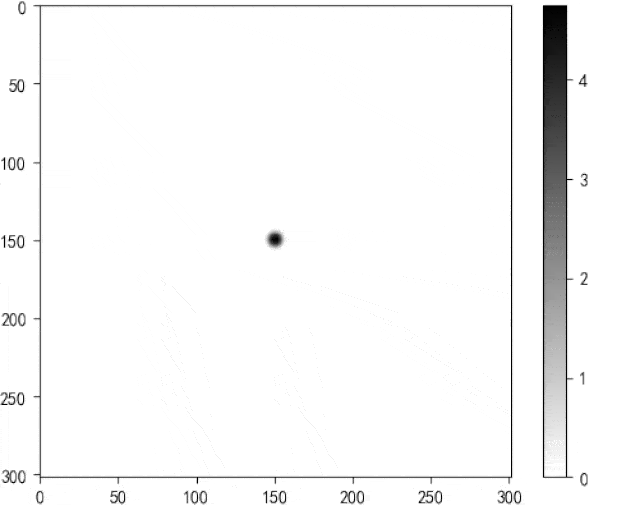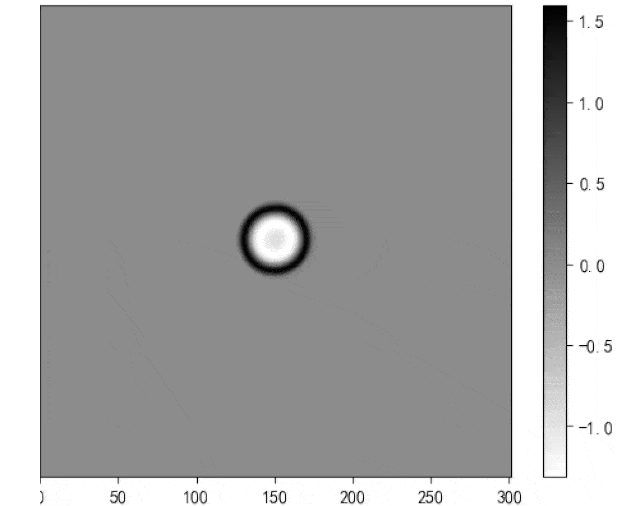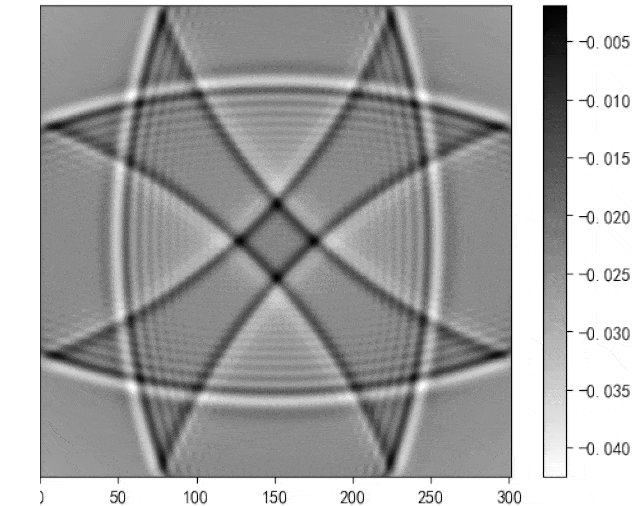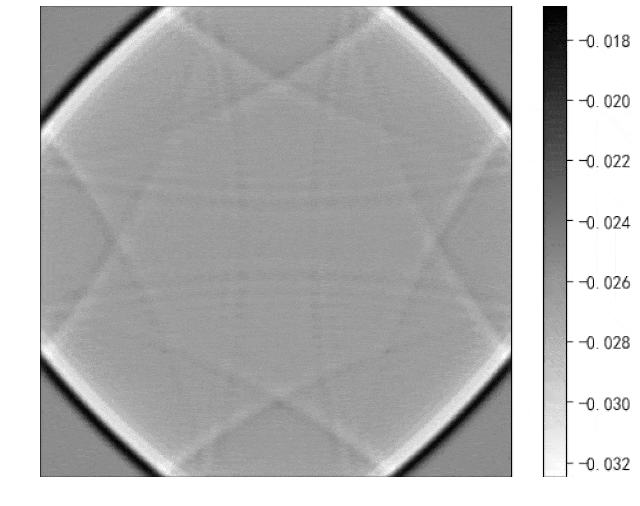
生成gif的代码如上，但有闪烁的问题如上图所示，本人无法解决，若有知道如何解决的，在线求教。