前文:
这个东西是我准备进攻一道Astar算法的八数码题目时,遇到的。
决定先搞懂这个,再进攻八数码(传说中那道不做人生不完整的题目)。
康托展开:
百度百科给出的定义是:康托展开是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩。 康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。
简单的说就是用来判断一个数的一个全排列在它所有的全排列中是第几个。
它的运算规则就是:
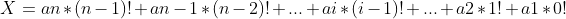
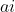
为整数,并且
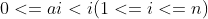
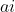
表示原数的第i位在当前未出现的元素中是排在第几个。
那这个东西有什么用呢?
假如你想要标记9的全排列,普通的方法就要开一个大小为10^9的数组,但是用康托展开只需要开大小为9!的数组就好了。
n位(0~n-1)全排列后,其康托展开唯一且最大约为n!,因此可以由更小的空间来储存这些排列。由公式可将X逆推出对应的全排列。它可以应用于哈希表中空间压缩,而且在搜索某些类型题时,将VIS数组量压缩。比如:八数码、魔板。
我们来举个例子:
可以求出n的全排列中第x大排列。
如n=5,x=96时:
首先用96-1得到95,说明x之前有95个排列.(将此数本身减去1)
用95去除4! 得到3余23,说明有3个数比第1位小,所以第一位是4.
用23去除3! 得到3余5,说明有3个数比第2位小,所以是4,但是4已出现过,因此是5.
用5去除2!得到2余1,类似地,这一位是3.
用1去除1!得到1余0,这一位是2.
最后一位只能是1.
所以这个数是45321。
再举个例子说明。
在 (1,2,3,4,5)5个数的排列组合中,计算 34152的康托展开值。
首位是3,
则小于3的数有两个,为1和2,a[5] = 2 ,则首位小于3的所有排列组合为a[5] * (5 - 1)!,第二位是4
则小于4的数有两个,为1和2,注意这里3并不能算,因为3已经在第一位,所以其实计算的是在第二位之后小于4的个数。因此a[4] = 2第三位是1
则在其之后小于1的数有0个,所以a[3] = 0第四位是5
则在其之后小于5的数有1个,为2,所以a[2] = 1 最后一位就不用计算啦,因为在它之后已经没有数了,所以 固定为0
根据公式:
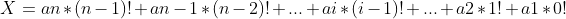
所以比34152小的组合有61个,即34152是排第62。
康托展开实现代码:
fact[10]; //fact[i]存储i的阶乘的值
//把数组s合并为一个状态num, k代表数组长度
void cantor (int s[], ll &num, int k)
{
num = 0;
for (int i = 0; i < k; i ++)
{
int cnt = 0;
for (int j = i + 1; j < k; j++)
if (s[i] > s[j]) cnt++;
num += fact[k - i - 1] * cnt;
}
}
康托展开的逆:
康托展开是一个全排列到自然数的双射,可以作为哈希函数。
所以当然也可以求逆运算了。
对于上述例子,在(1,2,3,4,5) 给出61可以算出起排列组合为34152。由上述的计算过程可以容易的逆推回来,具体过程如下:
用 61 / 4! = 2余13,说明
说明比首位小的数有2个,所以首位为3。用 13 / 3! = 2余1,说明
,说明在第二位之后小于第二位的数有2个,所以第二位为4。用 1 / 2! = 0余1,说明
,说明在第三位之后没有小于第三位的数,所以第三位为1。用 1 / 1! = 1余0,说明
,说明在第二位之后小于第四位的数有1个,所以第四位为5。
最后一位自然就是剩下的数2。
通过以上分析,所求排列组合为 34152。
康托逆展开代码实现:
int fac[] = {1,1,2,6,24,120,720,5040,40320};
//康托展开的逆运算,{1...n}的全排列,中的第k个数为s[]
void reverse_kangtuo(int n,int k,char s[])
{
int i, j, t, vst[8]={0};
--k;
for (i=0; i<n; i++)
{
t = k/fac[n-i-1];
for (j=1; j<=n; j++)
if (!vst[j])
{
if (t == 0) break;
--t;
}
s[i] = '0'+j;
vst[j] = 1;
k %= fac[n-i-1];
}
}





















