正交试验设计(Orthogonal experimental design)是研究多因素多水平的一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点,正交试验设计是一种基于正交表的、高效率、快速、经济的试验。
什么是因素(Factor):在一项试验中,凡欲考察的变量称为因素(变量)
什么是水平(位级)(Level):在试验范围内,因素被考察的值称为水平(变量的取值)
正交表的构成:
行数(Runs):正交表中的行的个数,即试验的次数。
因素数(Factors):正交表中列的个数。
水平数(Levels):任何单个因素能够取得的值的最大个数。正交表中的包含的值为从0到数“水平数-1”或从1到“水平数”
正交表的表示形式: L行数(水平数因素数)
正交表:
各列中出现的最大数字相同的正交表称为相同水平正交表。如L4(23)、L8(27)、L12(211)等各列中最大数字为2,称为两水平正交表;L9(34)、L27(313)等各列中最大数字为3,称为3水平正交表。凡是标准表,水平数都相等,且水平数只能取素数或素数幂。因此有7水平、9水平的标准表,没有6水平,8水平的标准表。
例如L9(34),它表示需做9次实验,最多可观察4个因素,每个因素均为3水平。
混合正交表:
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×24),即:L8(41×24)此表的5列中,有1列为4水平,4列为2水平。再如L16(44×23),L16(4×212)等都混合水平正交表。
正交表的两个特点:
正交表必须满足这两个特点,有一条不满足,就不是正交表。
1)每列中不同数字出现的次数相等。例如,在两水平正交表中,任何一列都有数码“1”与“2”,且任何一列中它们出现的次数是相等的;在三水平正交表中,任何一列都有“1”、“2”、“3”,且在任一列的出现数均相等。这一特点表明每个因素的每个水平与其它因素的每个水平参与试验的几率是完全相同的,从而保证了在各个水平中最大限度地排除了其它因素水平的干扰,能有效地比较试验结果并找出最优的试验条件。
2)在任意两列其横向组成的数字对中,每种数字对出现的次数相等。例如,在两水平正交表中,任何两列(同一横行内)有序对子共有4种:(1,1)、(1,2)、(2,1)、(2,2)。每种对数出现次数相等。在三水平情况下,任何两列(同一横行内)有序对共有9种,1.1、1.2、1.3、2.1、2.2、2.3、3.1、3.2、3.3,且每对出现数也均相等。这个特点保证了试验点均匀地分散在因素与水平的完全组合之中,因此具有很强的代表性。
以上两点充分的体现了正交表的两大优越性,即“均匀分散性,整齐可比”。通俗的说,每个因素的每个水平与另一个因素各水平各碰一次,这就是正交性。
混合正交表选择正交表的时候需满足:水平数>=max(水平1,水平2,...),因素数>=(因素1+因素2+因素3+…)
混合正交表选择正交表的示例:
我们分析一下:
1、被测项目中一共有四个被测对象(4个因素),每个被测对象的状态(水平数)都不一样。其中,A、C水平数均为3,B的水平数为4,D的水平数为2。
2、选择正交表:
本题,水平数>=max(3,4,2)=4,因素数>=4,查询附录中的正交表,只有L16(45)的行数最少,行数取最少的一个,比较适合。
3、最后选中正交表公式:L16(45)
另外,当水平数和因素数的具体值确定时,正确的行数(试验次数)的计算方法是:
试验次数(行数)=∑(每列水平数-1)+1
如:L18(36 *61)=(3-1)*6+(6-1)*1+1=18;L8(27)=(2-1)*7+1=8
如何查找正交表:
1、Technical Support (support.sas.com)
http://support.sas.com/techsup/technote/ts723_Designs.txt
2、查Dr. Genichi Taguchi设计的正交表
http://www.york.ac.uk/depts/maths/tables/orthogonal.htm
3、数理统计、试验设计等方面的书及附录中
用正交表设计测试用例
设计测试用例的步骤:
1、有哪些因素(变量)
2、每个因素有哪几个水平(变量的取值)
3、选择一个合适的正交表
4、把变量的值映射到表中
5、把每一行的各因素水平的组合作为一个测试用例
6、加上你认为可疑且没有在表中出现的用例组合
如何选择正交表
1、考虑因素(变量)的个数
2、考虑因素水平(变量的取值)的个数
3、考虑正交表的行数
4、取行数最少的一个
设计测试用例时的三种情况:
1、因素数(变量)、水平数(变量值)相符
水平数(变量的取值)相同、因素数(变量)刚好符合某一正交表,则直接套用正交表,得到用例。
例子:
对某人进行查询,假设查询某个人时有三个查询条件:
根据“姓名”进行查询
根据“身份证号码”查询
根据“手机号码”查询
考虑查询条件要么不填写,要么填写,此时可用正交表进行设计
① 因素数和水平数
有三个因素:姓名、身份证号、手机号码。每个因素有两个水平:
姓名:填、不填
身份证号:填、不填
手机号码:填、不填
② 选择正交表
表中的因素数>=3
表中至少有三个因素的水平数>=2
行数取最少的一个
结果:L4(2^3)
③ 变量映射
姓名:1→填写,2→不填写;
身份证号:1→填写,2→不填写;
手机号码:1→填写,2→不填写;
④ 用L4(2^3)设计的测试用例
测试用例如下:
1:填写姓名、填写身份证号、填写手机号
2:填写姓名、不填身份证号、不填手机号
3:不填姓名、填写身份证号、不填手机号
4:不填姓名、不填身份证号、填写手机号
⑤增补测试用例
5:不填姓名、不填身份证号、不填手机号
测试用例减少数:8→5
2、因素数不相同
水平数(变量的取值)与某正交表相同,但因素数(变量)却不相同,则取因素数最接近但略大于实际值的正交表表,套用之后,最后一列因素去掉即可。
例子:
兼容性测试:
操作系统:2000、XP、2003
浏览器:IE6.0、IE7.0、TT
杀毒软件:卡巴、金山、诺顿
如果全部进行测试的话,3^3=27个组合,需要进行27次测试。
① 因素数和水平数
有三个因素:
操作系统、浏览器、杀毒软件
每个因素有三个水平。
② 选择正交表
表中的因素数>=3
表中至少有三个因素的水平数>=3
行数取最少的一个
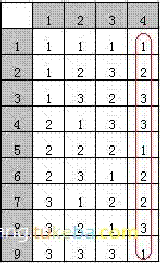
结果:L9(3^4),如下图:
③ 变量映射
操作系统:1→2000,2→XP,3→2003
浏览器:1→IE6.0,2→IE7.0,3→TT
杀毒软件:1→卡巴,2→金山,3→诺顿
④用L9(3^4)设计的测试用例
测试用例如下:
2000、IE6.0、卡巴
2000、IE7.0、诺顿
2000、TT、金山
XP、IE6.0、诺顿
XP、IE7.0、金山
XP、TT、卡巴
2003、IE6.0、金山
2003、IE7.0、卡巴
2003、TT、诺顿
⑤增补测试用例
由于目前IE6.0、XP、卡巴的使用量很高,故增添以下测试用例:
XP、IE6.0、金山
XP、IE6.0、卡巴
2003、IE6.0、卡巴
测试用例减少数:27→12
3、水平数不相同
因素(变量)与某正交表相同,但水平数(变量的取值)不相同。
例子:
假设有一个系统有5个独立的变量(A,B,C,D,E)。变量A和B都有两个取值(A1 、A2和B1、B2)。变量C和D都有三个可能的取值(C1、C2、C3和D1、D2、D3)。变量E有六个可能的取值(E1、E2、E3、E4、E5、E6)。
① 因素数和水平数
有五个因素(变量):
A、B、C、D和E
两个因素有两个水平(变量的取值)、两个因素有三个水平,一个因素有六个水平:
A:A1、A2
B:B1、B2
C:C1、C2、C3
D:D1、D2、D3
E:E1、E2、E3、E4、E5、E6
② 选择正交表
表中的因素数(变量)>=5
表中至少有二个因素的水平数(变量的取值)>=2
至少有另外二个因素的水平数>=3
还至少有另外一个因素的水平数>=6
行数取最少的一个:L49(7^8)或者L18(3^6 6^1))
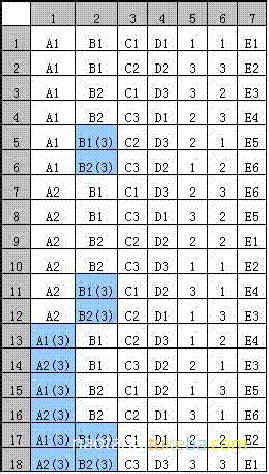
结果:L18(3^6 6^1)(如下图)
③ 变量映射
A:1→A1、2→A2
B:1→B1、2→B2
C:1→C1、2→C2、3→C3
D:1→D1、2→D2、3→D3
E1、2→E2、3→E3、4→E4、5→E5、6→E6
④ 用L18(3^6 6^1)设计的测试用例
略
测试用例减少数:216→18
加上一些可疑的情况(设为n个)为18+n,它比原来也少多了。