Lesson2
总述:这节课主要讲线性回归问题及其解法。用梯度下降的方法来训练参数,或用最小二乘法来直接计算参数。
1. 线性回归(linearregression),即假设特征和结果满足线性关系,模拟出数学模型,然后将该数学模型用于预测或分类。
假设我们有房屋销售的数据:
面积(m^2) | 卧室(间) | … | 销售价钱(万元) |
123 | 2 | … | 250 |
150 | 3 | … | 320 |
87 | 1 | … | 160 |
102 | 2 | … | 220 |
… | … | … | … |
我们用X1,X2,…,Xn 去描述feature里面的分量(一般会令X0=1),比如x1=房间的面积,x2=卧室个数等等,我们可以做出一个估计函数:
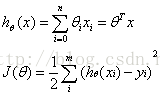
其中,J(θ)是损失函数。我们的目标是使J最小,此时再将求得的参数θ带入h(x)里即可得到所模拟的线性回归函数。显然这是一个线性规划求极小值问题。
2. 求参数的过程可用梯度下降法进行迭代求极值,也可用最小二乘法进行直接计算;(这里我想应该不会有童鞋问为什么不令h‘(x)=0求极值了吧~~)
(一)梯度下降法是按下面的流程进行的:
Step1:首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
Step2:改变θ的值,使得J(θ)按梯度下降的方向进行减少。
梯度方向由J(θ)对θ的偏导数确定,由于求的是极小值,所以:
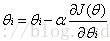
…………… (1)
其中:

式(1)就等价于:

…(2)
(m表示有m个训练样本,n表示有n个features,注:此处i是从1到m)
迭代更新的方式有两种:
一种是标准梯度下降,也就是对全部的训练数据求得误差后再对θ进行更新,即上面公式(2);
另外一种是随机梯度下降法(又称为增量梯度下降)。顾名思义,一定是用来改善梯度下降速度比较慢这个问题滴。我们把(2)式中的求和符号去掉,就得到了:

好啦,梯度下降法就讲到这里,再补充一下标准梯度下降和随机梯度下降的区别:
–标准梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查某个训练样例来更新的
–在标准梯度下降中,权值更新的每一步对多个样例求和,需要更多的计算
–标准梯度下降,由于使用真正的梯度,标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长
–如果标准误差曲面有多个局部极小值,随机梯度下降有时可能避免陷入这些局部极小值中
梯度下降法参考:
(二)用最小二乘法进行直接计算参数
我们将训练特征表示为X矩阵,结果表示成y向量,即

其中 表示第i个训练样本, 表示第i个训练样本里的第j个feature的值。

这时参数就可求出来了,但此方法要求X是列满秩的,而且求矩阵的逆比较慢。
(三)补充说明:
前面我们通过梯度下降的方法进行了线性回归,但是梯度下降有如下特点:
(1)需要预先选定学习速率 ;
(2)需要多次迭代;
(3)需要数据规范化(简单来说,它主要用来把所有特征值范围映射至同样的范围里面如(0,1)、(-1,1)等);
PS:
当Feature数量小于100000时使用最小二乘法;
当Feature数量大于100000时使用梯度下降法;























