python算法题中等难度 python经典算法题

1：求解最大连续子数组，A=[0,........,n-1],求A的连续子数组，使得该子数组和最大。

（1）：暴力搜索（时间复杂度O(n^3)）

#暴力搜索，三层循环，注意循环的起始变量
def MaxSubArray(A,n):
    res=[]
    MaxSum=A[0]
    for i in range(n):
        for j in range(i,n):
            curSum=0 #注意在求和之前赋初值
            for k in range(i,j):
                curSum+=A[k]
            if curSum>=MaxSum:
                MaxSum=curSum
                res=A[i:j]
                
    return res,MaxSum
 
if __name__=='__main__':
    A=[1,4,-5,9,8,3,-6]
    n=len(A)
    print(MaxSubArray(A,n))

（2）：分治法（时间复杂度O(nlogn)）。分治法，将数组从中间分开(递归实现)，那么最大子数组有三种情况。要么完全在数组的左半边；要么完全在数组的有半边；要么跨在分界点上。在这里完全左数组/完全右数组递归解决。跨在分界点上，实际上是左数组的最大后缀和右数组的最大前缀之和，因此以分界点向前扫描，向后扫描。

def MaxSubArray(A,left,right):
    
    if left==right: #递归出口
        return A[left]
    #分治
    middle=(left+right)//2
    m1=MaxSubArray(A,left,middle)#递归，右数组
    m2=MaxSubArray(A,middle+1,right)#递归，左数组
    #跨界点
    max_left=A[middle]
    now_left=A[middle]
    for i in range(middle-1,left,-1):#左数组的后缀
        now_left+=A[i]
        max_left==max(max_left,now_left)
        
    max_right=A[middle+1]
    now_right=A[middle+1]
    for i in range(middle+1+1,right):#右数组的前缀
        now_right+=A[i]
        max_right=max(max_right,now_right)
        
    m3=max_left+max_right#跨界点的和
    
    return max(m1,m2,m3) #返回最大和
        
if __name__=='__main__':
    A=[1,4,-5,9,8,3,-6]
    n=len(A)
    left=0
    right=n-1
    print(MaxSubArray(A,left,right))

2：查找旋转数组的最小值。假定一个排序数组以某元素为支点，原数组为[0,1,2,4,5,6,7],旋转后得到新的数组为[4,5,6,7,0,1,2].请找出旋转后的数组的最小值。

思路：旋转导致了数组被分为了两个有序序列。最小元素就是这两个序列的分界点。

用两个指针low和high,分别指向序列的第一个元素和最后一个元素。low到high为要搜索的序列（有问题序列），需要移动来缩小范围

建立一个中间位置middle，来将数组分成序列.来移动low和high.（也是一种二分的思想，利用双指针实现寻找分界点）。

def findMaxAraay(A,n):
    
    low=0
    high=n-1
    
    while low<high:
        middle=(low+high)//2 #middle实现的是范围的缩小
        
        if A[middle]>A[high]:#注意这里是middle>high
            low=middle+1         
        else:
            high=middle
            
    return A[low]

if __name__=='__main__':
    A=[4,5,6,7,0,1,2]
    n=len(A)
    print(findMaxAraay(A,n))

3：最长公共子序列：动态规划求解

Longest Common Subquence (LCS)： 最长公共子序列；可以用于两个序列的相似度问题，例如DNAl序列中有无基于的变异

两个序列X和Y的公共子序列中，长度最大的那个定义为X和Y的最长公共子序列。例如：13455和245576的最长公共子序列为455，其长度为3.

建立二维数组，存放元素为当前的功序列长度,其动态规划的递推公式为：

 

 

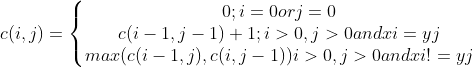
def LCS(s1,s2):
    
    m=len(s1)+1
    n=len(s2)+1
    matrix=[[0 for i in range(n)] for i in range(m)]
    #动态规划
    for i in range(1,m):
        for j in range(1,n):
            if s2[j-1]==s1[i-1]:
                matrix[i][j]=matrix[i-1][j-1]+1
            else:
                matrix[i][j]=max(matrix[i-1][j],matrix[i][j-1])                    
    return matrix[i][j],matrix #LCS长度,长度数组

def 

if __name__=='__main__':
    s1='ABCBDAB'
    s2='BDCABA'
    print(LCS(s1,s2))
    #若要得到具体的子序列，建立一个方向矩阵，之后回溯