nlp 一维卷积 一维卷积卷积核大小

文章目录

• 前言
• 一、卷积

• 1. 一维卷积
• 2. 二维卷积

• 二、特征图的尺寸计算

---

前言

  因为研究生方向是图像处理，所以开一个专题来记录自己的学习过程。小白刚接触，有错勿喷，欢迎讨论

---

一、卷积

滤波，通过滤波，能够得到感兴趣的信息，下面通过一些例子就能够看出来

1. 一维卷积

  《信号与系统》里面就讲了一维的卷积，计算公式为：

可以看到，两个（一维）信号的卷积，就是一个信号h(t)翻转后，从左到右滑动，与信号f(t)重叠区域的面积，如下图：

2. 二维卷积

  一维卷积不容易看出卷积的实质——“滤波”，但是二维卷积就可以有很好的看出来，如下图：

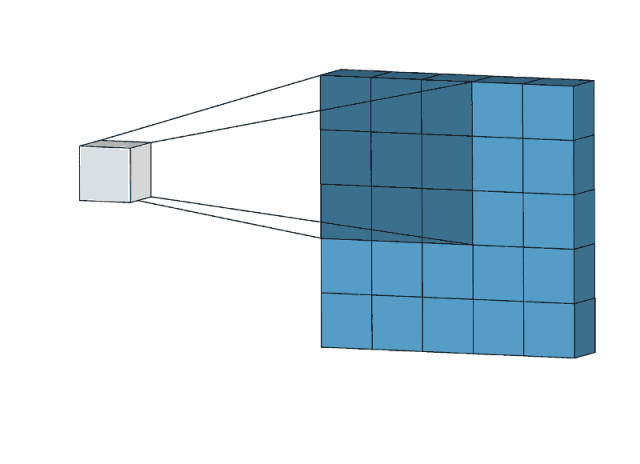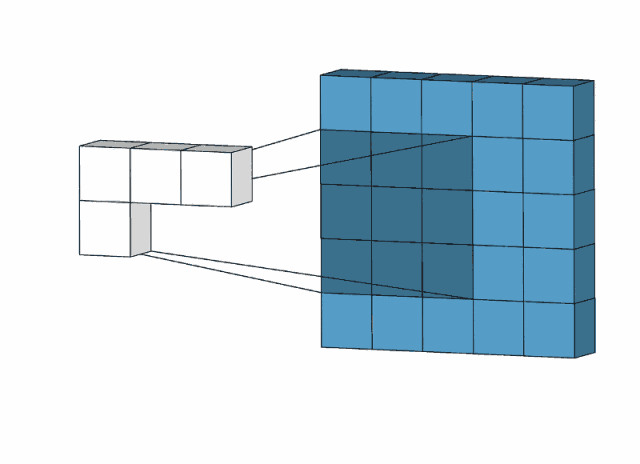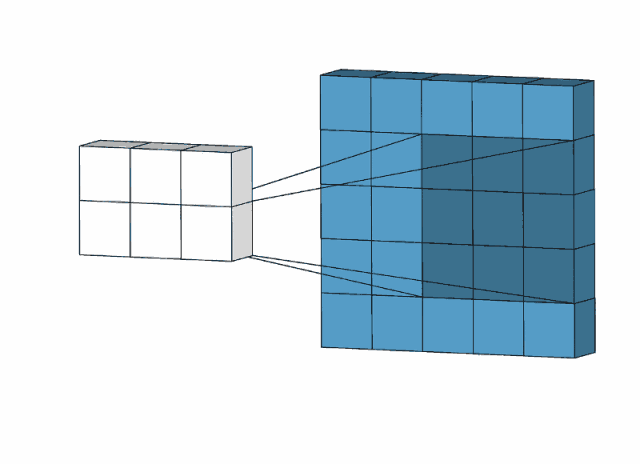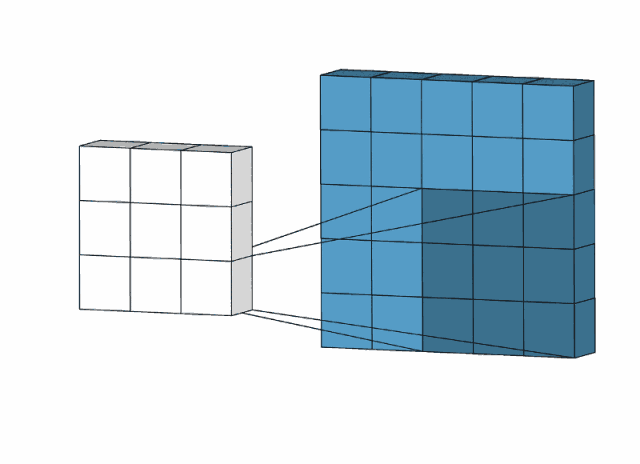
卷积核大小为3x3，在图像上滑动（相关和卷积类似，但是有很小的区别，将卷积核上下左右翻转，再沿着滑动方向做相关操作，得到的结果和直接做相关操作的结果一样），选择特定的卷积核，就可以提取一定的特征，比如下图中的锐化滤波卷积核：

就能够突出图像的细节部分，计算公式为：中间像素值 x 9 - 周围的8个像素差值之和，也就是说差别越大、滤波后细节更突出

二、特征图的尺寸计算

特征图，从二维卷积的示意图可以看出，卷积会改变图像的尺寸，以下图为例，卷积核尺寸为3x3，图像大小（空白方格）为7x7，卷积核移动的步长s = 2, 填充部分p = 1，卷积核的中心对齐最左上角的像素，开始滑动，横向滑动能够得到4个“像素”，纵向滑动能够得到4个“像素”，于是特征图尺寸为4x4

计算公式便为（公式中括号的意思为向下取整）：

将图中的数据代入公式，也是这个结果。如果碰到图像长宽不一样的情况，分别计算两个方向的尺寸就好