em算法和极大似然估计 极大似然估计代码

1、公式推导

逻辑回归中，最重要的公式推导就是将该问题转化为极大似然估计，然后求解，接着后面几个过程都实现了一些目的性的推导：

极大似然估计函数：

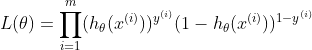
（1）这种连续相乘的表达式比较难求，可以两边取log，转化为相加的计算：

（2）依据定义，极大似然估计求得是最大的参数，习惯上，都是求最小值，所以可以给式子乘以-1，转化为求最小值（称为交叉熵损失函数）：

2、weka中对应代码及公式

理论和现实往往是有差距的，weka中代码的实现基本依据的是上述理论计算，但是同一个理论有多种实现办法，weka中代码的实现其实是较为复杂的，下面将详细介绍weka代码中极大似然估计这部分是如何实现计算的。

• 计算公式
• 实现代码

protected double objectiveFunction( double[] x )
{
	double	nll	= 0;                    /* -LogLikelihood */
	int	dim	= m_NumPredictors + 1;  /* Number of variables per class */

	for ( int i = 0; i < cls.length; i++ )  /* ith instance */

	{
		double[] exp = new double[m_NumClasses - 1];
		int index;
		for ( int offset = 0; offset < m_NumClasses - 1; offset++ )
		{
			index = offset * dim;
			for ( int j = 0; j < dim; j++ )
			{
				exp[offset] += m_Data[i][j] * x[index + j];
			}
		}
		double	max	= exp[Utils.maxIndex( exp )];
		double	denom	= Math.exp( -max );
		double	num;
		if ( cls[i] == m_NumClasses - 1 ) /* Class of this instance */
		{
			num = -max;
		} else {
			num = exp[cls[i]] - max;
		}
		for ( int offset = 0; offset < m_NumClasses - 1; offset++ )
		{
			denom += Math.exp( exp[offset] - max );
		}

		nll -= weights[i] * (num - Math.log( denom ) ); /* Weighted NLL */
	}

	/* Ridge: note that intercepts NOT included */
	for ( int offset = 0; offset < m_NumClasses - 1; offset++ )
	{
		for ( int r = 1; r < dim; r++ )
		{
			nll += m_Ridge * x[offset * dim + r] * x[offset * dim + r];
		}
	}

	return(nll);
}

•  测试代码

public static void main(String[] args) throws Exception {
		//Lg
		Logistic lg =new Logistic();
		Logistic.runClassifier(lg, "-t C:\\Users\\Administrator\\Desktop\\weather.numeric.arff".split(" "));
	}

@relation weather

@attribute outlook {sunny,overcast,rainy}
@attribute temperature numeric
@attribute humidity numeric
@attribute windy {TRUE,FALSE}
@attribute play {yes,no}

@data
sunny,85,85,FALSE,no
sunny,80,90,TRUE,no
overcast,83,86,FALSE,yes
rainy,70,96,FALSE,yes
rainy,68,80,FALSE,yes
rainy,65,70,TRUE,no
overcast,64,65,TRUE,yes
sunny,72,95,FALSE,no
sunny,69,70,FALSE,yes
rainy,75,80,FALSE,yes
sunny,75,70,TRUE,yes
overcast,72,90,TRUE,yes
overcast,81,75,FALSE,yes
rainy,71,91,TRUE,no

3、代码解析

• objectiveFunction(double[] x)中传递的可以认为是一个初始化的w（具体过程不详解）
• nll就是log(L())
• dim就是每个类别的属性个数+1，可以看到，如下展示：

之所以 上面的值为7，可以看下，实际上，因为outlook为类别型数据，weka自动把他拆成三个属性了，所以该值为7：

• 后面，接着是个大循环，for循环次数为14次，因为样本数为14
•  double[] exp = new double[m_NumClasses - 1]，这行代码，其实就是创建存储的数值的数组
• 下面这段代码比较重要，实际上这段代码实现了上面的多次相加，具体公式如下

int index;
for (int offset = 0; offset < m_NumClasses - 1; offset++) {
  index = offset * dim;
  for (int j = 0; j < dim; j++) {
      exp[offset] += m_Data[i][j] * x[index + j];
          }
}

• 下面这段代码实际上是计算公式中后面，后面那部分

double max = exp[Utils.maxIndex(exp)];
double denom = Math.exp(-max);
double num;
if (cls[i] == m_NumClasses - 1) { // Class of this instance
  num = -max;
} else {
  num = exp[cls[i]] - max;
 }


for (int offset = 0; offset < m_NumClasses - 1; offset++) {
  denom += Math.exp(exp[offset] - max);
}

可以看到，内部那个多项式之和，前两项可以先计算，然后后面那个再加上去就行。

• double max = exp[Utils.maxIndex(exp)],double denom = Math.exp(-max)，先求出多个类别里面最大的那个值，denom其实计算的就是sigmoid函数里面分母的部分
• if语句这段代码，其实计算的就是L的计算，其实默认max=Yij*log(Pij)，显然的，当Yij=1，num=-max；当Yij=0，num=log(1-Pij)-Yij*log(1-Pij)

for (int offset = 0; offset < m_NumClasses - 1; offset++) {
   denom += Math.exp(exp[offset] - max);
}

• 上面代码，则是计算sum(e^(wx+b))
• nll -= weights[i] * (num - Math.log(denom)); // Weighted NLL，这段代码，weights[i] 是权重，可以先不看，后面的计算其实是内部和式的最终值，num等于前两项相减，后面一项直接计算：

•  最后这部分是公式计算最后一部分，比较简单，不再详解：

// Ridge: note that intercepts NOT included
      for (int offset = 0; offset < m_NumClasses - 1; offset++) {
        for (int r = 1; r < dim; r++) {
          nll += m_Ridge * x[offset * dim + r] * x[offset * dim + r];
        }
      }

      return nll;