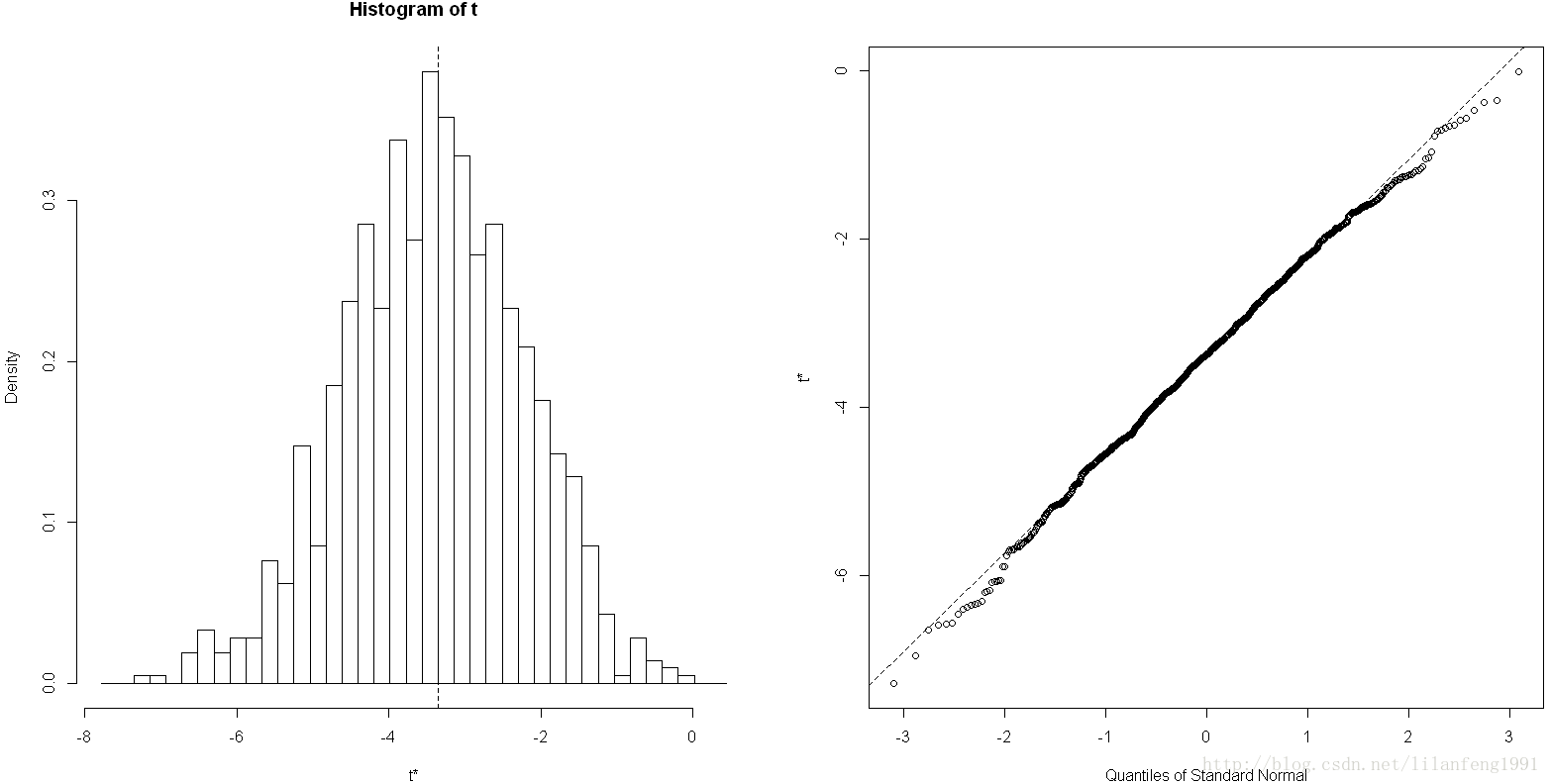
1.置换检验
当数据抽样于非正态分布时,如未知或混合分布、样本量过小、存在离群点、基于理论分布设计合适的统计检验过于复杂且数学上难以处理等情况,这时基于随机化和重抽样的统计方法可派上用场。
置换检验和自助法
置换检验
也称随机检验或重随机化检验
步骤:
(1) 与参数方法类似,计算观测数据的t统计量,称为t0;
(2) 将10个得分放在一个组中;
(3) 随机分配五个得分到A处理中,并分配五个得分到B处理中;
(4) 计算并记录新观测的t统计量;
(5) 对每一种可能随机分配重复(3)~(4)步,此处有252种可能的分配组合;
(6) 将252个统计量按升级序排列,这便是基于样本数据的经验分布;
(7) 若t0落在经验分布中间95%的外面,则在0.05的显著性水平下,拒绝两个处理组的总体均值相等的零假设。
置换方法和参数方法都计算了相同的t统计量。但置换方法并不是将统计量与理论分布进行比较,而是将其与转换观测数据后获得的经验进行比较,根据统计量值的极端性判断是否有理由拒绝零假设。
coin:对于独立性问题提供了一个非常全面的置换检验的框架;
lmPerm:专门用来做方差分析和回归分析的置换检验。
牢记:置换检验都是使用伪随机数来从所有可能的排列组合中进行抽样(当做近似检验时)。因此,每次检验的结果都有所不同。在R中设置随机数种子便可固定所生成的随机数。set.seed()
2、用coin包做置换检验
对于独立问题,coin包提供了一个进行置换检验的一般性框架。
可回答以下问题:
响应值与组的分配独立吗?
两个数值变量独立吗?
两个类别型变量独立吗?
相对于传统检验,提供可选置换检验的coin函数
检验 | coin函数 |
两样本和K样本置换检验 | oneway_test(y~A) |
含一个分层(区组)因子的两样本和K样本置换检验 | oneway_test(y~A|C) |
Wilcoxon-Mann-Whitney秩和检验 | wilcox_test(y~A) |
Kruskal-Wallis检验 | kruskal_test(y~A) |
Person卡方检验 | Chisq_test(A~B) |
Cochran-Mantel-Haenszel检验 | cmh_test(A~B|C) |
线性关联检验 | lbl_test(D~E) |
Spearman检验 | spearman_test(y~x) |
Friedman检验 | friendman_test(y~A|C) |
Wilcoxon符号秩检验 | wilcoxsign_test(y1~y2) |
function_name(formula,data,distribution)
formula描述的是要检验变量间的关系
data是一个数据框
distribution指定经验分布在零假设条件下的形式,可能值有exact,asymptotic和approximate
若distribution=“exact”,则在零假设条件下,分布的计算是精确的(即依据所有可能的排列组合);也可以根据它的渐进分布(distribution=“asymptotic”)或蒙特卡洛重抽样(distribution=”approximate(B=#)”)来做近似计算,其中#指所需重复的次数。distribution=”exact”当前仅可用于两样本问题。
在coin包中,类别型变量和序数变量必须分别转化为因子和有序因子,另数据以数据框形式存储。
3、两独立样本和K样本检验
(1)虚拟数据中的t检验与单因素置换检验
library(coin)
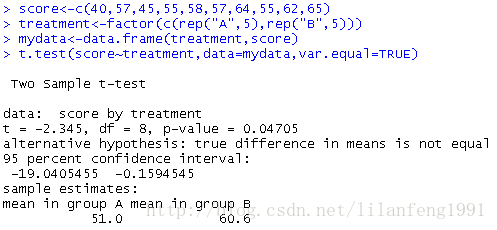
score<-c(40,57,45,55,58,57,64,55,62,65)
treatment<-factor(c(rep("A",5),rep("B",5)))
mydata<-data.frame(treatment,score)
t.test(score~treatment,data=mydata,var.equal=TRUE)
oneway_test(score~treatment,data=mydata,distribution="exact")

传统t检验存在显著性(p<0.05),而精确检验却表明差异并不显著(p>0.072),由于只有10个观测,故更倾向于相信转换检验结果,在做出最后结论之前,还要多收集些数据。
(2)Wilcoxon-Mann-WhitneyU检验
library(MASS)
UScrime<-transform(UScrime,So=factor(So)) #因coin包规定所有类别型变量都必须以因子形式编码,故将So转换为因子类型
wilcox_test(Prob~So,data=UScrime,distribution="exact") #wilcox_test()默认的也是精确分布

(3)K样本检验问题
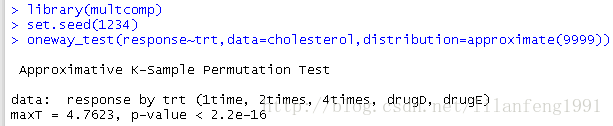
library(multcomp)
set.seed(1234)
oneway_test(response~trt,data=cholesterol,distribution=approximate(9999))
4. 列联表中的独立性
通过chisq_test()和cmh_test()函数,可用置换检验判断两类别型变量的独立性。
当数据可根据第三个类别型变量进行分层时,需要使用最后一个函数。
若变量都是有序型,可使用lbl_test()函数来检验是否存在线性趋势。
library(coin)
library(vcd)
Arthritis<-transform(Arthritis,Improved=as.factor(as.numeric(Improved)))#将Improved从一个有序因子变成一个分类因子?因有序因子,coin()将会生一个线性与线性趋势检验,而不是卡方检验。
set.seed(1234)
chisq_test(Treatment~Improved,data=Arthritis,distribution=approximate(B=9999))
5.数值变量间的独立性
spearman_test()函数提供了两数值变量的独立性置换检验。
states<-as.data.frame(state.x77)
set.seed(1234)
spearman_test(Illiteracy~Murder,data=states,distribution=approximate(B=9999))

6.两样本和K样本相关性检验
对于两配对组的置换检验,可使用wilcoxsign_test()函数;
多于两组时,使用friedman_test()函数
library(coin)
library(MASS)
wilcoxsign_test(U1~U2,data=UScrime,distribution="exact")

coin包提供了一个置换检验的一般性框架,可以分析一组变量相对于其他任意变量,是否与第二组变量(可根据一个区组变量分层)相互独立。特别地,independence_test()函数可让用户从置换角度来思考大部分传统检验,进而在面对无法用传统方法解决的问题时,使用户要吧自己建立新的统计检验。
详细内容可参见附带的文档:vignette("coin")
7.lmPerm包的置换检验
lmPerm包可作线性模型的置换检验
lmp()
lm()
aov()函数的修改版,能够进行置换检验,而非正态理论检验
lmp()和aovp()函数的参数与lm()和aov()函数类似,只额外添加了perm=参数。
perm=选项的可选值为“Exact”、“Prob”和“SPR”
Exact:根据所有可能的排列组合生成精确检验;
Prob:从所有可能的排列中不断抽样,直至估计的标准差在估计的p值0.1之下,判停准则由可选的Ca参数控制。
SPR:使用贯序概率来判断何时停止抽样。
注意:若观测数大于10,perm=“Exact”将自动默认转换为perm=”Prob”,因为精确检验只适用于小样本问题。
(1) 简单回归和多项式回归
简单线性回归的置换检验
install.packages("lmPerm")
library(lmPerm)
set.seed(1234)
fit<-lmp(weight~height,data=women,perm="Prob")
summary(fit)
(2)多元回归
library(lmPerm)
set.seed(1234)
states<-as.data.frame(state.x77)
fit<-lmp(Murder~Population+Illiteracy+Income+Frost,data=states,perm="Prob")
summary(fit)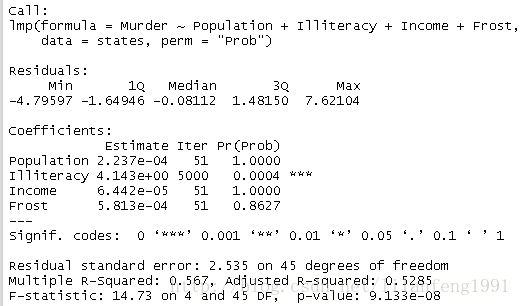
在正态理论中Population和Illiteracy均显著(P<0.05),而该置换检验中,Population不再显著。当两种方法所得结果不一致时,需要更加谨慎地审视数据,这很可能是因为违反了正态性假设或存在离群点。
(3) 单因素方差分析和协方差分析
单因素方差分析的置换检验
library(lmPerm)
library(multcomp)
set.seed(1234)
fit<-aovp(response~trt,data=cholesterol,perm="Prob")
summary(fit)

单因素协方差分析的置换检验
library(lmPerm)
set.seed(1234)
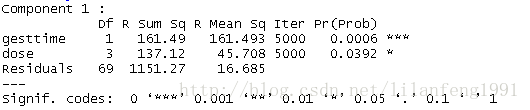
fit<-aovp(weight~gesttime+dose,data=litter,perm="Prob")
summary(fit)
(4) 双因素方差分析
library(lmPerm)
set.seed(1234)
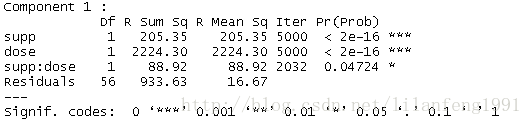
fit<-aovp(len~supp*dose,data=ToothGrowth,perm="Prob")
summary(fit)
(5) 置换检验点评
除coin和lmPerm包外,R还提供了其他可做转换检验的包
perm包能实现coin包中的部分功能,因此可作为coin包所得结果的验证;
corrperm包提供了有重复测量的相关性的置换检验;
logregperm包提供了Logistic回归的置换检验;
glmperm涵盖了广义线性模型的置换检验;
8.自助法
自助法,即从初始样本重复随机替换抽样,生成一个或一系列待检验统计量的经验分布,无需假设一个特定的理论分布,便可生成统计量的置信敬意,并能检验统计假设。
倘若假设均值的样本分布不是正态分布,可使用自助法:
(1) 从样本中随机选择10个观测,抽样后再放回。有些观测可能会被选择多次,有些可能一直都不会被选中;
(2) 计算并记录样本均值;
(3) 重复1和2一千次;
(4) 将1000个样本均值从小到大排序;
(5) 找出样本均值2.5%和97.5%的分位点,此时即初始位置和最末位置的第25个数,它们就限定了95%的置信区间。
样本均值很可能服从正态分布,自助法优势不太明显;但若不服从正态分布,自助法优势 十分明显。
9. Boot包中的自助法
一般来说,自助法有三个主要步骤:
(1) 写一个能返回待定统计量值的函数,若只有单个统计量(如中位数),函数应该返回一个数值;若有一列统计量(如一列回归系数),函数应该返回一个向量;
(2) 为生成R中自助法所需的有效统计量重复数,使用boot()函数对上面所写的函数进行处理;
(3) 使用boot.ci()函数获取第(2)步生成的统计量置信区间。
(1)对单个统计量使用自助法
rsq<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(summary(fit)$r.square)
}
library(boot)
set.seed(1234)
results<-boot(data=mtcars,statistic=rsq,R=1000,formula=mpg~wt+disp)
print(results)
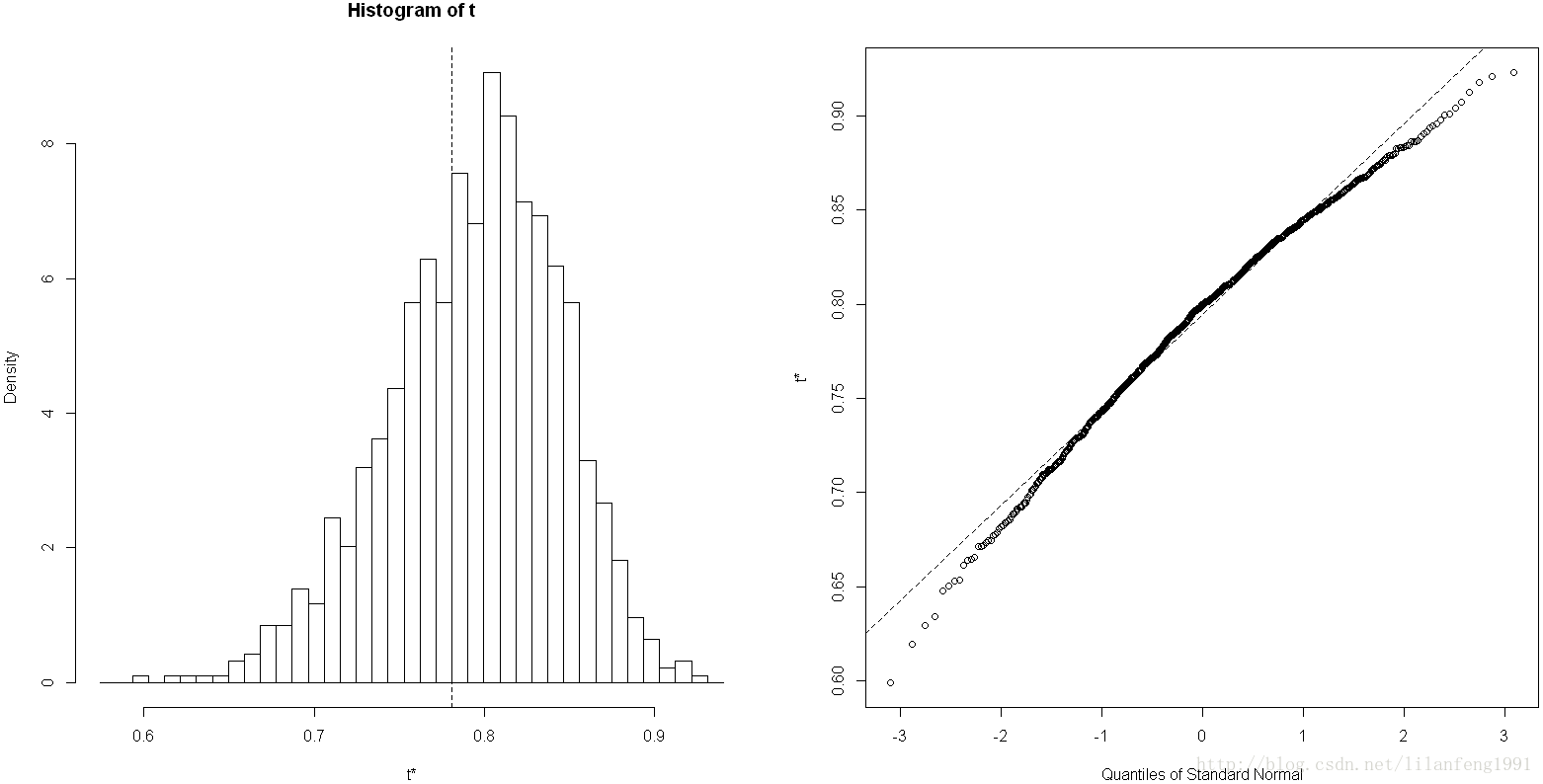
plot(results)
#可以看出自助的R的平方值不呈正态颁,它的95%的置信区间可通过如下代码获得
boot.ci(results,type=c("perc","bca"))

(2) 多个统计量的自助法
bs<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(coef(fit))
}
library(boot)
set.seed(1234)
results<-boot(data=mtcars,statistic=bs,R=1000,formula=mpg~wt+disp)
print(results)
boot(data=mtcars,statistic=bs,R=1000,formula=mpg~wt+disp)
plot(results,index=2)
boot.ci(results,type="bca",index=2)
boot.ci(results,type="bca",index=3)