5、电流控制方式
在永磁同步电动机的矢量控制系统中,需要根据不同的控制要求,采用不同的电流控制方式,协调地控制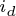 和
和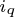
的大小, 在不同的电流控制方式下,电动机会呈现不同的特性,本文对各种电流控制方式进行介绍。
5.1 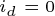 的控制方式
的控制方式
在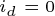 的控制方式中,无论
的控制方式中,无论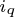 的大小如何,都保持
的大小如何,都保持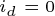 ,通过改变
,通过改变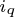 的值来实现对电动机转矩的控制。
的值来实现对电动机转矩的控制。
永磁同步电动机的电磁转矩方程为
![\tiny T_{e}=n_{p}\left [ \Psi _{f}i_{q}+\left ( L_{d}-L_{q} \right )i_{d}i_{q} \right ] android电流控制器 电流控制电流_控制系统_08](https://s2.51cto.com/images/blog/202306/06145959_647ed96feec3e2796.gif)
由于此时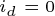 ,上式中的词组转矩变为0,电磁转矩的表达式可以进一步简化为
,上式中的词组转矩变为0,电磁转矩的表达式可以进一步简化为

而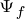 作为永磁体磁链,在电动机运行过程中保持不变,所以,通过控制转矩(交轴)电流分量
作为永磁体磁链,在电动机运行过程中保持不变,所以,通过控制转矩(交轴)电流分量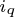 ,就可以实现对电动机转矩的控制。在这种控制方式中,当电动机处于稳态时,电流矢量
,就可以实现对电动机转矩的控制。在这种控制方式中,当电动机处于稳态时,电流矢量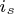 ,永磁体磁链矢量
,永磁体磁链矢量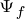 ,定子磁链矢量
,定子磁链矢量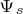 和定子电压矢量
和定子电压矢量 之间的关系如图11-9所示。
之间的关系如图11-9所示。

这种控制方式的优点是:由于定子电流的 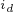 分量恒等于0,使得定子电流矢量与永磁体磁链矢量相互独立,控制系统的结构简单,调节器设计容易,转矩控制设计容易,转矩控制性能好,转矩脉动小,可获得较宽的调速范围。
分量恒等于0,使得定子电流矢量与永磁体磁链矢量相互独立,控制系统的结构简单,调节器设计容易,转矩控制设计容易,转矩控制性能好,转矩脉动小,可获得较宽的调速范围。
但是和异步电动机的矢量控制系统相比,在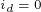 的控制方式中,定子磁链是随着转矩电流分量
的控制方式中,定子磁链是随着转矩电流分量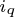 的增加而增加的,因此,这种控制方式又存在以下几个缺点:
的增加而增加的,因此,这种控制方式又存在以下几个缺点:
(1)在同一转速下,当负载增加时,交轴电流分量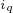 和负载成正比增加, 使得气隙磁链和反电动势都加大,迫使定子电压为克服反电动势而升高。为了保证调速系统在大负载下有足够的电源电压,变频器需要有足够的电压裕量。
和负载成正比增加, 使得气隙磁链和反电动势都加大,迫使定子电压为克服反电动势而升高。为了保证调速系统在大负载下有足够的电源电压,变频器需要有足够的电压裕量。
(2)当负载增加时,定子电压矢量和定子电流矢量的夹角也会增大,造成电动机的功率因数降低。
(3)当凸极率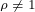 时,在
时,在 的控制方式下,电动机无磁阻转矩输出,降低了电动机的转矩输出能力。对于凸极式转子结构,单位电流产生的电磁转矩不是最大的。而对于隐极式转子结构,其交轴、直轴电感相同,无论
的控制方式下,电动机无磁阻转矩输出,降低了电动机的转矩输出能力。对于凸极式转子结构,单位电流产生的电磁转矩不是最大的。而对于隐极式转子结构,其交轴、直轴电感相同,无论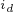 是否为零都不会产生磁阻转矩,所以这种控制方式对隐极式转子结构也就是最大转矩电流比控制。
是否为零都不会产生磁阻转矩,所以这种控制方式对隐极式转子结构也就是最大转矩电流比控制。
由于存在以上缺点,导致这种控制方式的使用范围受到限制。为了克服这些问题,需要根据实际工况,按照一定的原则协调控制定子电流的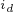 和
和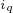 分量,而不是在调速过程中始终保持
分量,而不是在调速过程中始终保持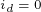 不变。
不变。
5.2 MTPA控制方式
永磁同步电动机的MTPA控制方式即最大转矩电流比(Maximum Torque-per-Ampere,MTPA)控制方式,其含义是,在该控制方式下,幅值一定的定子电流产生的转矩最大,等价于对应相同的电磁转矩,在该控制方式下所需的定子电流最小,进而对应的电动机铜损也最小。
由电磁转矩表达式可以得到具有最大转矩电流比对应的电流相角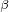 的值,
的值,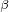 的表达式为
的表达式为
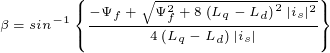
式中,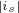 ——定子电流的幅值。
——定子电流的幅值。
如果电动机的转子为隐极式结构,则有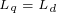 ,上式的分母等于0,则不能按照上式来确定
,上式的分母等于0,则不能按照上式来确定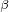 角的值,但是,根据前面的讨论可知,对于隐极式转子结构,
角的值,但是,根据前面的讨论可知,对于隐极式转子结构,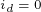 的控制方式和MTPA控制方式是一样的。
的控制方式和MTPA控制方式是一样的。
对于凸极式转子结构,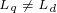 ,在MTPA控制方式中,根据上式和
,在MTPA控制方式中,根据上式和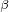 角的定义可知,交轴电流
角的定义可知,交轴电流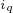 和直轴电流
和直轴电流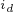 之间的关系为
之间的关系为

在实际的系统运行过程中,只要利用转速调节器的输出(即 轴电流的给定值
轴电流的给定值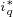 ),根据上式计算出
),根据上式计算出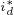 ,最后通过两个电流调节器的控制作用,使得实际电流值等于两个电流给定值,就实现了MTPA控制方式下的矢量控制系统。
,最后通过两个电流调节器的控制作用,使得实际电流值等于两个电流给定值,就实现了MTPA控制方式下的矢量控制系统。
下图给出了前两式表示的在MTPA控制方式下的电流矢量的变化轨迹,还给出了恒转矩和恒电流曲线。
由图中可以看出,在电磁转矩分别为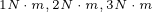 时,电动机分别稳定运行在
时,电动机分别稳定运行在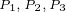 ,这三个点分别为恒转矩曲线和恒电流曲线的切点,
,这三个点分别为恒转矩曲线和恒电流曲线的切点,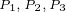 对应的电流值分别为
对应的电流值分别为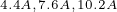 。另外,根据MTPA控制方式的定义可知,当电流幅值分别为
。另外,根据MTPA控制方式的定义可知,当电流幅值分别为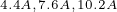 时,能够产生的最大转矩分别为
时,能够产生的最大转矩分别为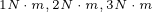 。
。
下图仅给出了在第二象限内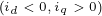 的特性曲线,可以证明,相应的曲线是关于
的特性曲线,可以证明,相应的曲线是关于 轴对称的,因此,很容易得到在第三象限内
轴对称的,因此,很容易得到在第三象限内 曲线的变化情况。在第二象限内曲线描述的是,当转矩为正时电动机的运行情况,而在第三象限内曲线描述的是当转矩为负时电动机的运行情况。
曲线的变化情况。在第二象限内曲线描述的是,当转矩为正时电动机的运行情况,而在第三象限内曲线描述的是当转矩为负时电动机的运行情况。

图11-10 在MTPA控制方式下的电流矢量轨迹图
5.3 MTPV控制方式
MTPV控制方式即最大转矩电压比控制方式(Maximum Torque-per-Voltage,MTPV),其含义是在该控制方式下,幅值一定的定子电压产生的转矩最大,等价于对应相同的电磁转矩,在该方式下所需的定子电压最小,进而对应的电动机铁损也最小。
MTPV对应的工作点除了具有电压最小的特性之外,该点的定子磁链的幅值也最小。当调速系统具有最大转矩电压比时,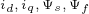
之间的关系如下式所示。
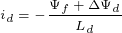
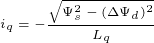
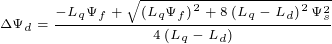
式中,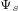 ——定子磁链的幅值。
——定子磁链的幅值。
在实际系统中,确定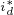 的过程为:首先把转速调节器的输出
的过程为:首先把转速调节器的输出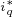 代入到上式中,此时上式就构成了一个未知数为
代入到上式中,此时上式就构成了一个未知数为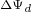 和
和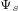 的方程组;然后,解该方程组得到
的方程组;然后,解该方程组得到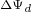 和
和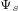 的值;最后,把
的值;最后,把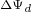 和
和 代入上式中,就得到了
代入上式中,就得到了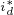 的值。
的值。
图11-11给出了由上式表示的在MTPV控制方式下的电流矢量的变化轨迹,还给出了恒转矩曲线和恒磁链曲线,注意恒磁链曲线具有椭圆的形状。

由图中可以看出,随着转矩的递减,最大转矩点沿着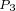 点
点
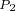 点
点
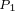 点运动,
点运动,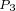 点为
点为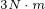 恒转矩曲线与
恒转矩曲线与
恒磁链曲线的切点,表示当磁链为 时,电动机能够输出的最大转矩为
时,电动机能够输出的最大转矩为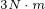 。
。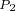 对应
对应 恒磁链曲线上的最大转折点,
恒磁链曲线上的最大转折点,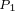 对应
对应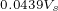 恒磁链曲线上的最大转矩点。图中的
恒磁链曲线上的最大转矩点。图中的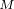 点对应的电流为
点对应的电流为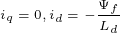 ,此时对应的磁链幅值为0。
,此时对应的磁链幅值为0。
5.4 弱磁控制方式
根据磁链方程式,可知计算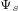 的公式为
的公式为
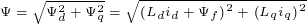
上式中永磁体磁链 是不可控制的,在运行过程中保持不变,但是,可以利用
是不可控制的,在运行过程中保持不变,但是,可以利用 轴定子电流
轴定子电流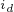 的电枢反应来调节磁链分量
的电枢反应来调节磁链分量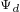 ,当
,当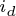 为负时,
为负时,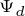 减小,
减小,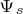 也随之减小,这种减弱
也随之减小,这种减弱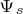 的控制方法就被称为弱磁控制。弱磁控制通常用于高速区,使定子感应电动势的幅值(忽略定子电阻压降)等于逆变器能够输出的最高电压的幅值
的控制方法就被称为弱磁控制。弱磁控制通常用于高速区,使定子感应电动势的幅值(忽略定子电阻压降)等于逆变器能够输出的最高电压的幅值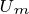 。
。
忽略定子电阻压降,且在稳态有
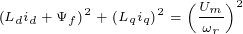
电流分量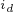 和
和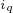 的关系为
的关系为
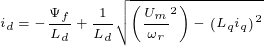
下图给出了上式描述的电流矢量的变化轨迹,同时给出了在不同转速下最大电压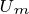 对应的椭圆形曲线,在不同转速下最大电压曲线是不一样的,随着转速的升高,最大电压曲线呈收缩趋势,当转速无限大时,椭圆收缩于M点。椭圆形曲线的中心位于图中的M点处,下图中的M点于5.3节图中的M点为同一点。
对应的椭圆形曲线,在不同转速下最大电压曲线是不一样的,随着转速的升高,最大电压曲线呈收缩趋势,当转速无限大时,椭圆收缩于M点。椭圆形曲线的中心位于图中的M点处,下图中的M点于5.3节图中的M点为同一点。

在运行过程中, 根据上式控制电流矢量位于电压限制椭圆上,以保证逆变器输出最大电压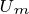 ,由图中可以看出,电动机转速为
,由图中可以看出,电动机转速为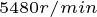 ,当转矩由
,当转矩由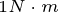 增加到
增加到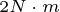 再增加到
再增加到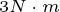 时,电流矢量的运动轨迹为
时,电流矢量的运动轨迹为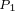 点
点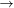
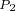 点
点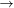
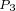 点,且再转矩变化的过程中,逆变器输出的电压幅值保持不变。
点,且再转矩变化的过程中,逆变器输出的电压幅值保持不变。
5.5 最小功率损耗控制
在永磁同步电动机的电压方程式的基础上,再考虑电动机的铁损,可以得到电动机在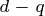 坐标系上的等效电路,如下图所示。图中
坐标系上的等效电路,如下图所示。图中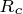 为铁损电阻;
为铁损电阻;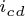 和
和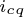 分别为
分别为 轴和
轴和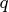 轴的铁损电流分量;
轴的铁损电流分量;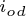 和
和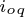 分别为
分别为 轴和
轴和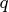 轴的磁化电流分量。由图中可以看出,在等效电路中,电流
轴的磁化电流分量。由图中可以看出,在等效电路中,电流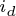 和
和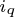 都被分解成铁损电流分量和磁化电流分量两部分。
都被分解成铁损电流分量和磁化电流分量两部分。

利用铁损电阻和铁损电流,电动机的铁损损耗可以表示为
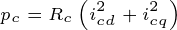
铁损电阻并不是一个常数,而是一个随运行频率变化而变化的量,它与频率的关系可建模为
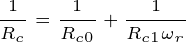
式中,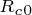 ——电涡流损耗电阻;
——电涡流损耗电阻;
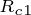 ——磁滞损耗电阻。
——磁滞损耗电阻。
根据永磁同步电动机的等效电路图可以得到损耗最小时的电流矢量,该电流矢量是电磁转矩和转速的函数,在某一转速和转矩下,该电流矢量可以使电动机的功率损耗最小,其随转速和转矩变化的轨迹称为最小损耗曲线,简记为LM曲线。
在下图中,给出了最小功率损耗控制方式下的电流矢量轨迹,由图中可以看出,LM轨迹具有以下特点:
(1)由于在电动机静止时,其铁损为零,同时忽略PWM的谐波损耗,此时电动机的损耗只剩下铜损一项,因此,当
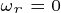
时,LM电流矢量轨迹和MTPA电流矢量轨迹是重合的。
(2)当电动机的转速增加时,在恒转矩曲线时,LM电流矢量轨迹向左移动。
(3)当转速增加到无限大时,电动机的铜损远远小于铁损,可以忽略不计,LM电流矢量轨迹和MTPV电流矢量轨迹是重合的。
下图给出了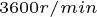 时的LM电流矢量变化轨迹,由图中可以看出,电磁转矩由
时的LM电流矢量变化轨迹,由图中可以看出,电磁转矩由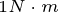 增加到
增加到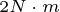 再增加到
再增加到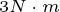 时,电流矢量的运动轨迹为
时,电流矢量的运动轨迹为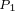 点
点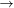
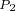 点
点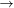
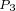 点。当转矩固定为
点。当转矩固定为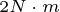 不变,而转速由
不变,而转速由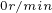 逐渐增加时,电流矢量的运动轨迹为
逐渐增加时,电流矢量的运动轨迹为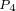 点
点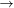
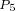 点
点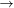
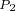 点
点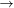
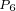 点
点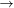
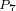 点。
点。
在实际控制中,不同工况下的 轴和
轴和 轴的电流给定值,可以通过公式计算的方法获得,也可以利用实验的方法获得,得到的电流给定值可以存储在表中,或者把这些数值拟合成近似函数,供程序实时调用。
轴的电流给定值,可以通过公式计算的方法获得,也可以利用实验的方法获得,得到的电流给定值可以存储在表中,或者把这些数值拟合成近似函数,供程序实时调用。

5.6 各种控制方式的比较
下图给出了在以上5种控制方式下的电流矢量的变化情况。

在弱磁控制方式和最小功率损耗控制方式下,电流矢量的变化轨迹是随着转速的变化而变化的,上图给出了当 时,在这两种控制方式下的电流矢量的变化轨迹,并且假设在若此控制方式下的最大输出电压
时,在这两种控制方式下的电流矢量的变化轨迹,并且假设在若此控制方式下的最大输出电压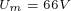 。
。
点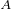 到
到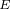 分别位于MTPA控制、MTPV控制、FW控制、LM控制和
分别位于MTPA控制、MTPV控制、FW控制、LM控制和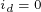 控制的电流矢量轨迹中,且这些点对应的转矩都为
控制的电流矢量轨迹中,且这些点对应的转矩都为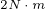 。由图中可以看出,
。由图中可以看出,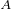 点对应的电流幅值最小;
点对应的电流幅值最小;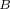 点对应的感应电动势和定子磁链最小;
点对应的感应电动势和定子磁链最小; 点的感应电动势保持在
点的感应电动势保持在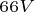 ;
;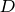 点的电动机损耗最小,电动机效率达到最优;
点的电动机损耗最小,电动机效率达到最优;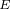 点的
点的 轴电流值为0,在该控制方式下,转矩和
轴电流值为0,在该控制方式下,转矩和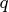 轴电流成正比。
轴电流成正比。
除了以上提到的几种控制方式以外,还存在其他的控制方式,如单位功率因数控制方式,在该控制方式下, 轴和
轴和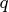 轴电流的协调变化关系可以由电机在
轴电流的协调变化关系可以由电机在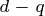 坐标系上的数学模型得到,感兴趣的读者可以参考相关文献。由图中可以看出,在不同的控制方式下,电动机的稳态运行点有很大的不同,因此,在实际的调速系统中,应该根据控制目标和运行条件来选择合适的控制方式。
坐标系上的数学模型得到,感兴趣的读者可以参考相关文献。由图中可以看出,在不同的控制方式下,电动机的稳态运行点有很大的不同,因此,在实际的调速系统中,应该根据控制目标和运行条件来选择合适的控制方式。























