一 梯度
函数 z = f(x, y) 梯度表示为
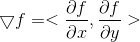
,其梯度方向始终指向函数较大值处。函数 z = f(x, y) 几何图形需要三维空间表示,为了更方便观察函数,可以使用二维平面上等高线表示函数。例如:函数
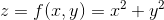
等高线可表示为XY平面上的同心圆。同理,函数 f(x, y, z) 梯度表示为
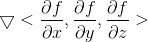
,可以使用三为空间等值面表示函数。
函数梯度与等高线(或等值面)关系:任意点函数梯度向量垂直于该点所在等高线(或等值面)。
针对二维函数,其推导如下:
1)函数 z = f(x, y) 在XY平面上取任意一条等高线 f(x, y) = c ,将该条等高线上点表示为变量 t 的函数:x = x(t), y = y(t),等高线可表示为 f(x(t), y(t)) = c;
2)在等高线上取任意一点,沿等高线移动一小段距离,函数值保持不变,则有:
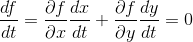
,
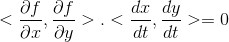
,
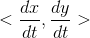
表示沿登高线切线方向,则可证明梯度垂直于等高线。 针对三维函数,思路与二维函数基本一致。首先选择等值面 f(x, y, z) = c , 在等值面上任意选取一条曲线:x = x(t), y = y(t), z = z(t),等值面上任意一条曲线可表示为f(x(t), y(t), z(t)) = c 。然后沿该曲线移动一小段距离,函数值保持不变,则有
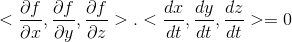
,
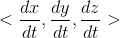
为等值面上任意一条曲线切线方向,表明梯度与等值面切线方向垂直,可证明梯度垂直于等值面。
二 方向梯度
针对多元函数,使用偏导可以得到坐标轴方向上函数变化情况。使用方向梯度,可以得到任意方向上函数变化情况。定义任意方向单位向量
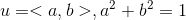
,沿单位向量移动单位距离,坐标轴变化情况为:
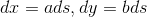
。通过建立x,y 与 s 的复合关系,函数 f(x, y) 可改写为 f(x(s), y(s)), 则有
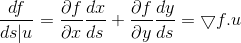
。 因此,沿u方向上的方向梯度等于函数沿坐标轴上梯度向量与单位方向向量的点积。进一步观察可得:
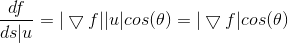
,其中
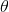
为函数梯度向量与方向向量夹角。当梯度向量与方向向量平行时,函数在该点取得最大方向导数(反向为负值);当梯度方向与方向导数反向时,函数在该点方向导数为零。
心得:根据以上推导,方向导数不可能在两个正交方向上均取得较大值,而在角点检测中,使用自相关函数检测在两个正交方向上均有较大变化的点,则该点应该为一个奇点(不可导)。
在图像处理中,一般使用梯度方向作为边缘方向,而图像并非严格函数,通常会得到一些偏差较大边缘方向,是否可以通过考察等高线上梯度值来获得更好的边缘方向?
三 拉格朗日乘数法
求解函数 f(x, y, z) 在限定条件 g(x, y, z) = c 时取得极值。
方法一:通过 g(x, y, z) = c 消除一个变量,可以将函数 f(x, y, z) 改写成二元函数,使用一阶偏导寻找到极值点。
方法二:使用拉格朗日乘数法,当函数 f(x, y, z) 取得极值时,满足
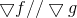
,g(x, y, z) = c,结合以上条件即可求解极值点,推导如下: 1)在 g(x, y, z) = c 等值面上任意取一点,该点如果为函数 f(x, y, z) 上的极值点,则沿该点任意方向上,其方向梯度满足:
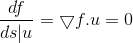
,则在 f 上梯度方向垂直于g所在切平面;
2)g 上梯度方向垂直于g所在切平面;
3)
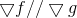
。 例:求解f(x,y)极值,
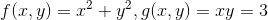
,根据拉格朗日乘数法,建立如下关系:
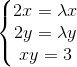
,可求解函数 f 在限定 g 下的极值。
拉格朗日乘数法无法区分极大值或极小值,一般通过比较得到最大值或最小值。
参考:多变量微积分 Prof. Denis Auroux





















