一、ARIMA
1、平稳性:要求序列的均值和方差不发生明显变化
大部分数据都是弱平稳数据,未来某时刻的t值就要依赖它过去的信息,具有依赖性。严平稳不考虑。
2、差分法
时间序列在 t 与 t-1 时刻的差值
一般大多使用一阶差分,二阶差分,高于这个会丢失原始数据的许多信息。
二、自回归模型(AR)
描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测
1、要求:自回归模型必须满足平稳性要求
p 阶自回归过程公式定义:


是当前值
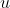
是常数项 P 是阶数
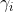
是自相关系数
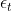
是误差
2、限制
如果自相关系数小于0.5 则不宜采用,只适用于预测与自身前期先关的现象
三、移动平均模型(MA)
移动平均模型关注的是自回归模型中误差项的累加
定义:

q 是移动平均模型阶数,
移动平均法能有效的消除预测中的随机波动
四、自回归移动平均模型(ARMA)
自回归与移动平均结合
定义:

五、差分自回归移动平均模型(ARIMA)
AR 是自回归 , p 是自回归项数 ;
MA 是移动平均, q 是 移动平均项数;
d 是能让时间序列成为平稳时间所做的差分次数。
1、原理:
将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
六、自相关函数ACF
有序的随机变量序列与其自身相比较
自相关函数反映了同一序列在不同时序的取值之间的相关性
公式定义:

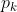
的取值为[-1,1]
七、偏自相关函数(PACF)
对于一个平稳AR(p)模型,求出滞后 k 自相关系数 p(k) 时,实际上得到的并不是 下 x(t) 与 x(t-k) 之间的单纯的相关关系。
x(t) 同时还会受到中间 k-1 个随机变量 x(t-1)、x(t-2)、 ......x(t-k+1)的影响。 而这 k-1 个随机变量又都和 x(t-k) 具有相关关系。所以自相关系数 p(k) 里实际掺杂了其他变量对 x(t) 与 x(t-k) 的影响。
而偏自相关系数PACF是严格的这两个变量之间的相关性。
八、ARIMA( p, d, q)阶数确定

截尾:落在置信区间内(95%的点都符合该规则)





















