BCD:binary-coded decimal(BCD码也称二进码十进数)。
即bcd代码,用4位二进制数来表示1位十进制数中的0~9这10个数码,是一种二进制的数字编码形式,用二进制编码的十进制代码。
说明:BCD码这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。这种编码技巧最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免去使计算机作浮点运算时所耗费的时间。此外,对于其他需要高精确度的计算,BCD编码亦很常用。
一、几点说明
类别分为:有权码和无权码
常用的类型:有权bcd8421码和有权2421码,及无权余3码。
何谓之有权:数学中的“权”代表不等精度观测值在计算未知量的最可靠值时所占的“比重”或“份额”。所以有权BCD码的每一位都有确定的权值,用有权BCD码表示十进制数0~9时,要求BCD码按式
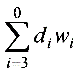
(di和wi分别为BCD码第i位上的数字和权值)所求之和等于所表示的十进制数。例如8421码,其4个二进制位由高到低,权值分别为8、4、2、1。
压缩bcd与非压缩bcd:的区别—— 压缩BCD码的每一位用4位二进制表示,一个字节表示两位十进制数。例如10010110B表示十进制数96D;非压缩BCD码用1个字节表示一位十进制数,高四位总是0000,低4位的0000~1001表示0~9.例如00001000B表示十进制数8.

十进制数“36”用非压缩的BCD码表示为“00000011 00000110”而用压缩的BCD码表示为“0011 0110”。其中00000011和0011代表3,00000110和0110代表6,以此类推(一般地,压缩BCD码比较常用,可以节约存储空间。)
二、常见类别
8421:最基本和最常用的(重点学习),它和四位自然二进制码相似,各位的权值为8、4、2、1,故称为有权BCD码。和四位自然二进制码不同的是,它只选用了四位二进制码中前10组代码,即用0000~1001分别代表它所对应的十进制数,余下的六组代码不用。
5421和2421:它们从高位到低位的权值分别为5、4、2、1和2、4、2、1。这两种有权BCD码中,有的十进制数码存在两种加权方法,例如,5421 BCD码中的数码5,既可以用1000表示,也可以用0101表示;2421 BCD码中的数码6,既可以用1100表示, 也可以用0110表示。这说明5421 BCD码和2421 BCD码的编码方案都不是惟一的,表1-2只列出了一种编码方案。
上表中2421 BCD码的10个数码中,0和9、1和8、2和7、3和6、4和5的代码对应位恰好一个是0时,另一个就是1。就称0和9、1和8互为反码。
余3 码:余3码是8421 BCD码的每个码组加3(0011)形成的。常用于BCD码的运算电路中(所以不在此深入)。
十进制数 | 8421码 | 5421码 | 2421码 | 余3码 | 余3循环码 |
0 | 0000 | 0000 | 0000 | 0011 | 0010 |
1 | 0001 | 0001 | 0001 | 0100 | 0110 |
2 | 0010 | 0010 | 0010 | 0101 | 0111 |
3 | 0011 | 0011 | 0011 | 0110 | 0101 |
4 | 0100 | 0100 | 0100 | 0111 | 0100 |
5 | 0101 | 1000 | 1011 | 1000 | 1100 |
6 | 0110 | 1001 | 1100 | 1001 | 1101 |
7 | 0111 | 1010 | 1101 | 1010 | 1111 |
8 | 1000 | 1011 | 1110 | 1011 | 1110 |
9 | 1001 | 1100 | 1111 | 1100 | 1010 |
三、重点学习之8424码(日常所说的BCD码大都是指8421BCD码形式)
BCD码的运算法则
BCD码的运算规则:BCD码是十进制数,而运算器对数据做加减运算时,都是按二进制运算规则进行处理的。这样,当将 BCD码传送给运算器进行运算时,其结果需要修正。修正的规则是:当两个BCD码相加,如果和等于或小于 1001(即十进制数9),不需要修正;如果相加之和在 1010 到1111(即十六进制数 0AH~0FH)之间,则需加 6 进行修正;如果相加时,本位产生了进位,也需加 6 进行修正。这样做的原因是,机器按二进制相加,所以 4 位二进制数相加时,是按“逢十六进一”的原则进行运算的,而实质上是 2 个十进制数相加,应该按“逢十进一”的原则相加,16 与10相差 6,所以当和超过 9或有进位时,都要加 6 进行修正。下面举例说明。
举个例子:
321的8421码就是
3 2 1
0011 0010 0001
原因:0011=8x0+4x0+1x2+1x1=3 0010=8x0+4x0+2x1+1x0=2. 0001=8x0+4x0+2x0+1x1=1
具体:
bcd码是十位二进制码, 也就是将十进制的数字转化为二进制, 但是和普通的转化有一点不同, 每一个十进制的数字0-9都对应着一个四位的二进制码,对应关系如下: 十进制0 对应 二进制0000 ;十进制1 对应二进制0001 ....... 9 1001 接下来的10就有两个上述的码来表示 10 表示为00010000 也就是BCD码是遇见1001就产生进位,不象普通的二进制码,到1111才产生进位10000
举例:
某二进制无符号数11101010,转换为三位非压缩BCD数,按百位、十位和个位的顺序表示,应为
A.00000001 00000011 00000111 B. 00000011 00000001 00000111
C.00000010 00000011 00000100 D. 00000011 00000001 00001001
解:(1)11101010转换为十进制:234
(2)按百位、十位和个位的顺序表示,应为
附注:压缩BCD码与非压缩BCD码的区别—— 压缩BCD码的每一位用4位二进制表示,一个字节表示两位十进制数。例如10010110B表示十进制数96D;非压缩BCD码用1个字节表示一位十进制数,高四位总是0000,低4位的0000~1001表示0~9.例如00001000B表示十进制数8.
BCD是指用二进制来表示十进制数的编码,即:用4位二进制来表示一位十进制数,因此4位二进制数表示最大的十进制数9(1001)。
一个四位的BCD码不能够表达十进制的两位数,因此当数字大于九时,我们需要用八位BCD码来表示。高位只需要逢九进一即可。
十进制是逢十进一,而十六进制是逢十六进一,它们之间的每次进位差6,所以一个十进制数要转换成BCD码,要先算清多进位的位数。
当两个BCD码相加,如果和等于或小于 1001(即十进制数9),不需要修正。
如果相加之和在 1010 到1111(即十六进制数 0AH~0FH)之间,则需加 6 进行修正
十进制99进位了99/10=9次,每次进位和十六进制进位相比差6,所以一共差了9×6=54,即BCD码为:99+54=153(十六进制:0X99)。BCD码转化成十进制码也一样原理。、





















