pytorch 激活函数 复数 pytorch自定义激活函数

之前的文章已经讲了很多，下面我们来深入讲解激活函数：

放大看一下：

相关激活函数的导数：

激活函数案例

假设你想尝试各种激活函数，来找出哪个激活函数是最好的。会怎么做呢?通常我们执行超参数优化——这可以使用scikit-learn的GridSearchCV函数来完成。但是我们想要比较，所以我们选择一些超参数并保持它们不变，同时改变激活函数。

让我给你们简单介绍一下，我在这里要做的：

使用不同上网激活函数训练相同的神经网络神经模型

利用每个激活函数的结果，绘制一个损失和准确性图。

我们从导入我们所需要的一切开始。注意这里使用了4个库;Tensorflow, numpy, matplotlib和keras。

1. 导入相关库

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.utils.np_utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPooling2D, Activation, LeakyReLU
from keras.layers.noise import AlphaDropout
from keras.utils.generic_utils import get_custom_objects
from keras import backend as K
from keras.optimizers import Adam

2. 导入数据

从这里开始，我们想要加载一个数据集来运行这个实验;让我们选择MNIST数据集。我们可以直接从Keras导入。

(x_train,y_train),(x_test,y_test)=mnist.load_data()

3. 数据预处理

这很好，但我们想对数据进行预处理，使其标准化。我们通过使用许多函数来实现这一点，主要是.reshape图像并除以/= 255，即最大RGB值。最后，我们用to_categorical()对数据进行one-hot编码。

def preprocess_mnist(x_train,y_train,x_test,y_test):
	# 将所有图像reshape为28*28
	x_train=x_train.reshape(x_train.shape[0],28,28,1)
	x_test=x_test.reshape(x_test.shape[0],28,28,1)
	input_shape=(28,28,1)
	
	# 将数据转为float类型
	x_train=x_train.astype("float32")
	x_test=x_test.astype("float32")
	
	# 归一化
	x_train/=255.
	x_test/=255.
	# one-hot编码
	y_train=to_categorical(y_train)
	y_test=to_categorical(y_test)
	return x_train,y_train,x_test,y_test,input_shape

x_train,y_train,x_test,y_test,input_shape=preprocess_mnist(x_train,y_train,x_test,y_test)

4. 构建模型

现在我们已经对数据进行了预处理，现在可以构建模型并定义Keras要运行的一些东西了。让我们从卷积神经网络模型本身开始。对于SELU激活函数，我们有一个特殊的情况，我们需要使用kernel初始化器lecun_normal和dropout的特殊形式AlphaDropout()。

def build_cnn(activation, dropout_rate, optimizer):
    model = Sequential()
    if (activation == "selu"):
        model.add(Conv2D(32, kernel_size=(3, 3), activation=activation, input_shape=input_shape,
                         kernel_initializer="lecun_normal"))
        model.add(Conv2D(64, (3, 3), activation=activation, kernel_initializer="lecun_normal"))
        model.add(MaxPooling2D(pool_size=(2, 2)))
        model.add(AlphaDropout(0.25))
        model.add(Flatten())
        model.add(Dense(128, activation=activation, kernel_initializer="lecun_normal"))
        model.add(AlphaDropout(0.5))
        model.add(Dense(10, activation="softmax"))
    else:
        model.add(Conv2D(32, kernel_size=(3, 3), activation=activation, input_shape=input_shape))
        model.add(Conv2D(64, (3, 3), activation=activation))
        model.add(MaxPooling2D(pool_size=(2, 2)))
        model.add(AlphaDropout(0.25))
        model.add(Flatten())
        model.add(Dense(128, activation=activation))
        model.add(AlphaDropout(0.5))
        model.add(Dense(10, activation="softmax"))

    model.compile(loss="binary_crossentropy", optimizer=optimizer, metrics=["accuracy"])
    return model

5. 构建GELU激活函数

GELU 函数在 Keras 中尚不存在。但是向 Keras 添加新的激活函数非常容易。

def gelu(x):
    return 0.5 * x * (1 + tf.tanh(tf.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x, 3))))

# 添加gelu，这样我们就可以将其作为字符串使用
get_custom_objects().update({'gelu': Activation(gelu)})

# 添加leaky-relu，这样我们就可以将其作为字符串使用
get_custom_objects().update({"leaky-relu": Activation(LeakyReLU(alpha=0.2))})

act_func = ["sigmoid", "relu", "elu", "leaky-relu", "selu", "gelu"]

6. 训练

现在，我们准备使用在act_func数组中定义的不同激活函数来训练模型。我们对每个激活函数运行一个简单的for循环，并将其结果添加到一个数组中。

result=[]
for activation in act_func:
	print("\nTraining with -->{0}<-- activation function\n".format(activation))
	model=build_cnn(activation=activation,dropout_rate=0.2,optimizer=Adam(clipvalue=0.5))
	history=model.fit(x_train, y_train, validation_split=0.2, batch_size=128,epochs=20,verbose=1,validation_data=(x_test,y_test))
	result.append(history)
	K.clear_session()
	del model
print(result)

7. 绘制结果

由此，我们可以绘制从model.fit()中获得的每个激活函数的结果。 现在我们已经准备好绘制数据了，我使用matplotlib编写了一些简短的代码：

new_act_arr=act_func[1:]
new_results=result[1:]
def plot_act_func_results(results,activation_functions=[]):
	plt.figure(figsize=(10,10))
	# 绘制验证准确率
	for act_func in results:
		plt.plot(act_func.history["val_acc"])
	plt.title("Model Accuracy")
	plt.ylabel("Test Accuracy")
	plt.xlabel("Epoch")
	plt.legend(activation_functions)
	plt.show()
	# 绘制验证集损失值
	plt.figure(figsize=(10,10))
	for act_func in results:
		plt.plot(act_func.history["val_loss"])
	plt.title("Model Loss")
	plt.ylabel("Test Loss")
	plt.xlabel("Epoch")
	plt.legend(activation_functions)
	plt.show()
plot_act_func_results(new_results,new_act_arr)

激活函数解析

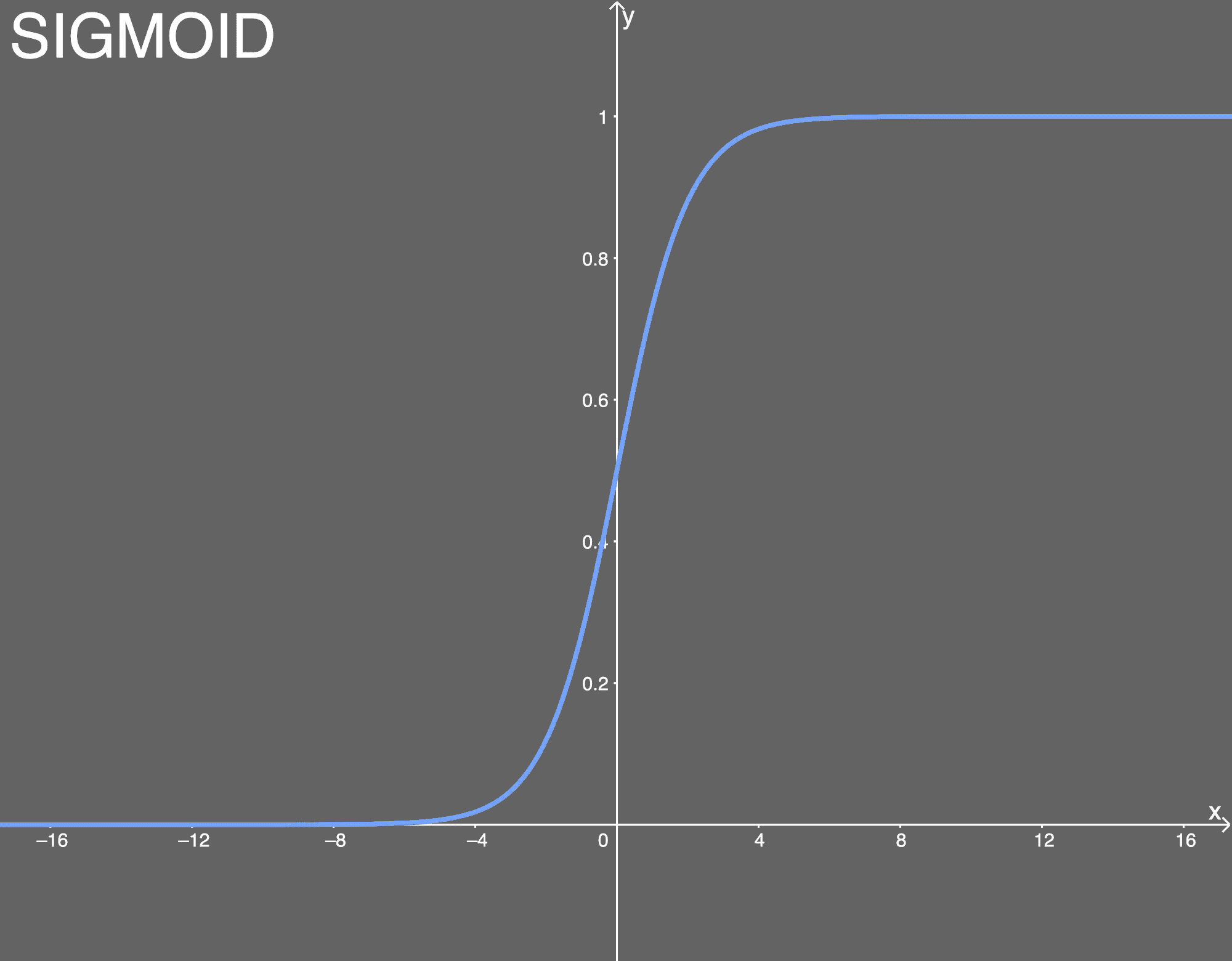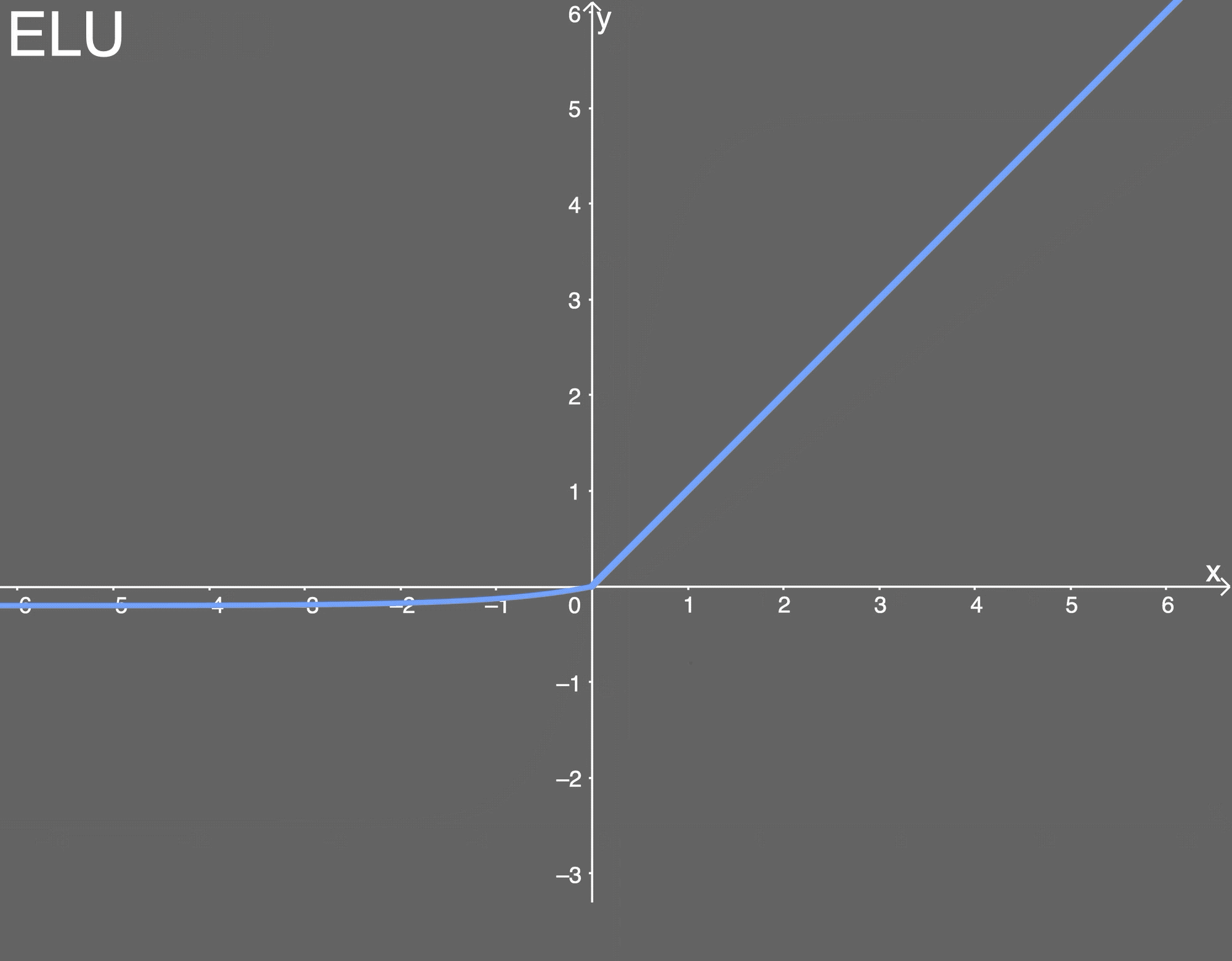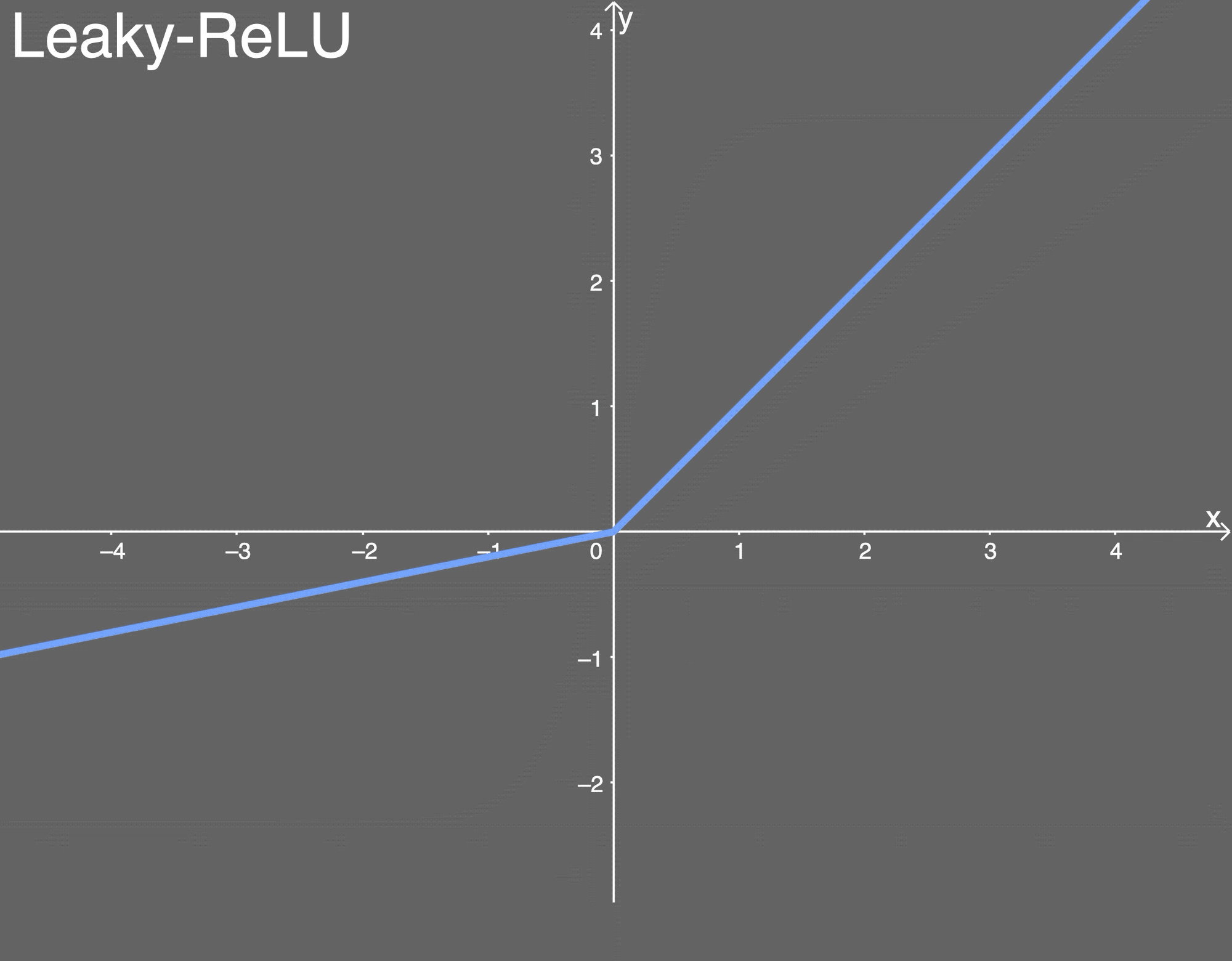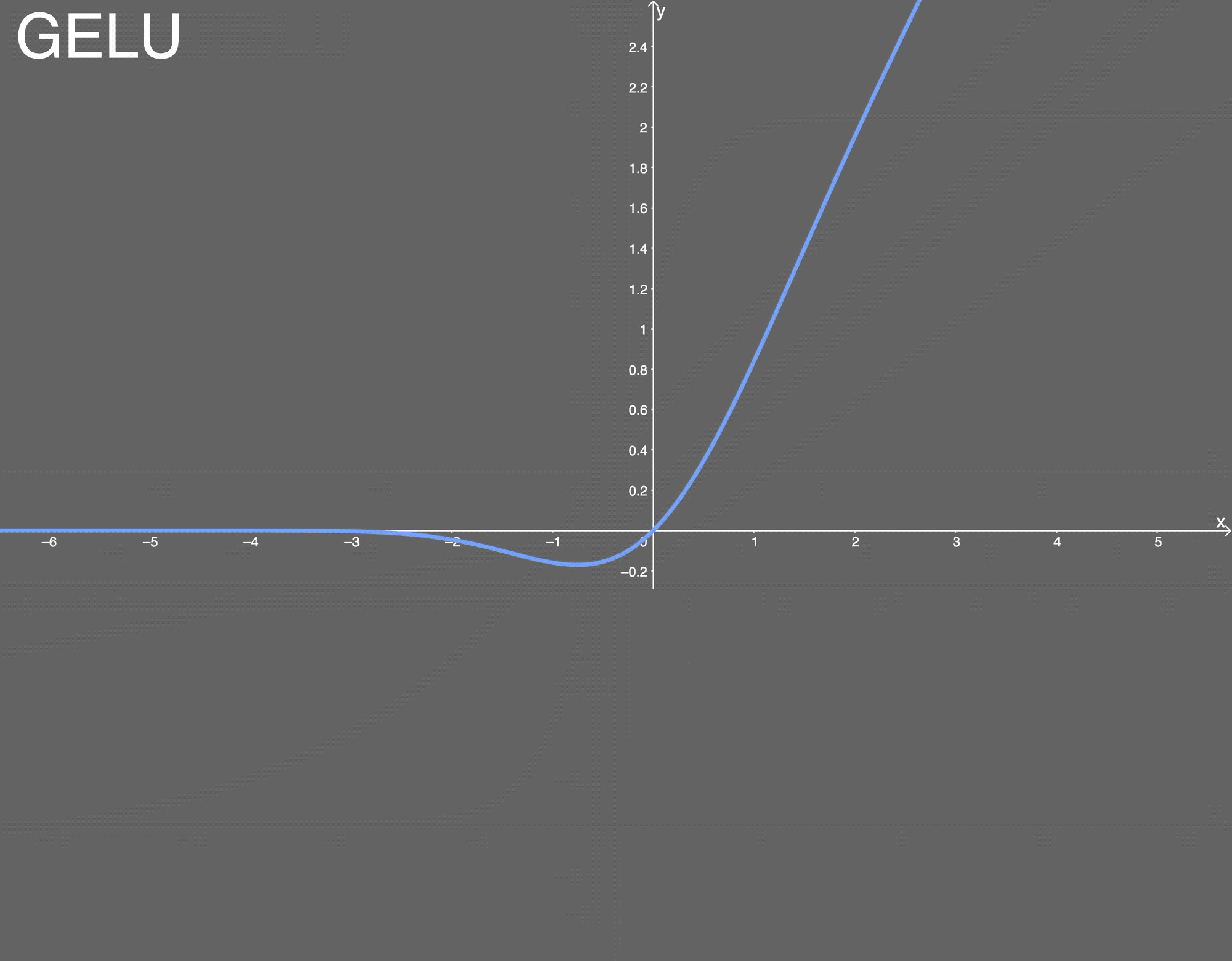
1. sigmoid激活函数

导数为：

优点：

（1）便于求导的平滑函数；

（2）能压缩数据，保证数据幅度不会有问题；

缺点：

（1）容易出现梯度消失（gradient vanishing）的现象：当激活函数接近饱和区时，变化太缓慢，导数接近0，根据后向传递的数学依据是微积分求导的链式法则，当前导数需要之前各层导数的乘积，几个比较小的数相乘，导数结果很接近0，从而无法完成深层网络的训练。

（2）Sigmoid的输出不是0均值（zero-centered）的：这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。以 f=sigmoid(wx+b)为例， 假设输入均为正数（或负数），那么对w的导数总是正数（或负数），这样在反向传播过程中要么都往正方向更新，要么都往负方向更新，导致有一种捆绑效果，使得收敛缓慢。

（3）幂运算相对耗时

3. tanh激活函数



4. tanh 是对 sigmoid 的平移和收缩: tanh(x)=2⋅σ(2x)−1



5. tanh 作为激活函数的特点： 相比 Sigmoid 函数， （1） tanh 的输出范围时(-1, 1)， 解决了 Sigmoid 函数的不是 zero-centered 输出问题； （2） 幂运算的问题仍然存在； （3） tanh 导数范围在(0, 1)之间， 相比 sigmoid 的(0, 0.25)， 梯度消失（ gradient vanishing） 问题会得到缓解， 但仍然还会存在。 （4）以零为中心的影响：如果当前参数(w0,w1)的最佳优化方向是(+d0, -d1),则根据反向传播计算公式,我们希望 x0 和 x1 符号相反。但是如果上一级神经元采用 Sigmoid 函数作为激活函数，sigmoid不以0为中心，输出值恒为正，那么我们无法进行最快的参数更新，而是走 Z 字形逼近最优解。
7. relu激活函数

优点： 相比于 sigmoid， 由于稀疏性， 时间和空间复杂度更低； 不涉及成本更高的指数运算； 能避免梯度消失问题。

缺点： 引入了死亡 ReLU 问题， 即网络的大部分分量都永远不会更新。 但这有时候也是一个优势； ReLU 不能避免梯度爆炸问题。

如果在计算梯度时有太多值都低于 0 会怎样呢？ 我们会得到相当多不会更新的权重和偏置， 因为其更新的量为 0。

5. elu激活函数



6. ELU函数如下图所示$\alpha$值为0.2。



7. ELU的导数为：





9. 优点： 能避免死亡 ReLU 问题； 能得到负值输出， 这能帮助网络向正确的方向推动权重和偏置变化； 在计算梯度时能得到激活， 而不是让它们等于 0。 缺点： 由于包含指数运算， 所以计算时间更长； 无法避免梯度爆炸问题； 神经网络不学习α值。
11. leaky-relu激活函数



12. Leaky ReLU画在这里，假设$\alpha$是0.2:



13. LReLU的导数为：





15. 优点： 类似 ELU， Leaky ReLU 也能避免死亡 ReLU 问题， 因为其在计算导数时允许较小的梯度； 由于不包含指数运算， 所以计算速度比 ELU 快。 缺点： 无法避免梯度爆炸问题； 神经网络不学习 $\alpha$
17. selu激活函数





19. 如果输入值 x 大于 0， 则输出值为 x 乘以 λ； 如果输入值 x 小于 0， 则会得到一个奇异函数— —它随 x 增大而增大并趋近于 x 为 0 时的值 0.0848。 本质上看， 当 x 小于 0 时， 先用$\alpha$乘以 x 值的指数， 再减去 $\alpha$， 然后乘以 λ 值。



20. SELU的导数为：

SELU 激活能够对神经网络进行自归一化（self-normalizing） 。 这是什么意思？ 首先， 我们先看看什么是归一化（ normalization） 。 简单来说， 归一化首先是减去均值， 然后除以标准差。 因此， 经过归一化之后， 网络的组（权重、 偏置和激活） 的均值为 0， 标准差为 1。 而这正是 SELU 激活函数的输出值。均值为 0 且标准差为 1 又如何呢？ 在初始化函数为 lecun_normal 的假设下， 网络参数会被初始化一个正态分布（或高斯分布） ， 然后在SELU 的情况下， 网络会在论文中描述的范围内完全地归一化。 本质上看，当乘或加这样的网络分量时， 网络仍被视为符合高斯分布。 我们就称之为归一化。 反过来， 这又意味着整个网络及其最后一层的输出也是归一化的。

注意实际应用这个激活函数时， 必须使用 lecun_normal 进行权重初始化。 如果希望应用 dropout， 则应当使用AlphaDropout。 优点： 内部归一化的速度比外部归一化快， 这意味着网络能更快收敛； 不可能出现梯度消失或爆炸问题。 缺点： 这个激活函数相对较新——需要更多论文比较性地探索其在 CNN 和 RNN 等架构中应用。

7. gelu激活函数 优点： 似乎是 NLP 领域的当前最佳； 尤其在 Transformer 模型中表现最好；能避免梯度消失问题。 缺点： 尽管是 2016 年提出的， 但在实际应用中还是一个相当新颖的激活函数。

为什么深度神经网络很难训练

在训练深度神经网络时，你可能会遇到两个挑战。

1. 梯度消失 与sigmoid函数类似，某些激活函数将输入空间压缩到0到1之间的小输出空间。sigmoid函数的输入发生很大的变化，输出仅发生很小的变化。因此，导数变得很小。对于只有几层使用这些激活的浅层网络来说，这不是一个大问题。然而，当使用更多层时，它可能会导致梯度太小，训练无法有效地工作。
2. 梯度爆炸 梯度爆炸是指在训练过程中显著的误差梯度累积并导致神经网络模型权值进行非常大的更新的问题。 当梯度呈爆炸式增长，学习无法完成时，网络就会变得不稳定。 权值也可能变得非常大，以至于溢出并产生NaN值。 梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。
3. 解决方法 a. 解决梯度消失需要考虑几个方面: 1）权重初始化 使用合适的方式初始化权重, 如ReLU使用MSRA的初始化方式, tanh使用xavier初始化方式. 2） 激活函数选择 激活函数要选择ReLU等梯度累乘稳定的. 3）学习率 一种训练优化方式是对输入做白化操作(包括正规化和去相关), 目的是可以选择更大的学习率。现代深度学习网络中常使用Batch Normalization(包括正规化步骤,但不含去相关)。 b. 梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。

梯度函数的选择

您需要根据您正在解决的预测问题的类型(具体地说，预测变量的类型)匹配输出层的激活函数。 根据经验，您可以从使用ReLU激活函数开始，如果ReLU不能提供最佳结果，则可以转移到其他激活函数。 这里有一些其他的指导方针来帮助你。 1）ReLU激活函数只能在隐藏层中使用。 2）Sigmoid/Logistic和Tanh激活函数不应该在隐藏层中使用，因为它们会使模型在训练过程中更容易出现问题(由于梯度消失)。 3）Swish函数用于深度大于40层的神经网络。

最后，根据你要解决的预测问题的类型，为你的输出层选择激活函数的一些规则: 1）回归问题：线性激活函数 2）二分类：Sigmoid/Logistic激活函数 3）多分类：Softmax激活函数 4）多标签分类：Sigmoid激活函数 隐层中使用的激活函数通常是根据神经网络结构的类型来选择的。 5）卷积神经网络：ReLU激活函数 6）循环神经网络：Tanh或者Sigmoid激活函数