支持向量机SVM 这一知识点在机器学习中是非常重要的一个知识点,笔者想要通过自己的学习记录总结下来方便日后复习。
学习资料参考:周志华老师的《机器学习》第六章、李航老师的《统计学习方法》的第七章。
文章中许多公式及图片来自于书中,这篇总结是根据笔者的基础会补充一些笔者不懂的知识点。
支持向量机(support vector machines,SVM)是一种二类分类模型。它的基本模型是 定义在特征空间上的间隔最大的线性分类器。它通过引入一个超平面,将样本点分隔成两簇,以达到预测样本类别的目的。而SVM算法的主要过程就是求出这个分离超平面。
超平面:
我们将SVM学习得到的分离超平面记为

W*是超平面的法向量,b*是超平面的截距。分离超平 面对应于方程w·x+b=0,它由法向量w和截距b决定,可用(w,b)来表示。分离超平面将特 征空间划分为两部分,一部分是正类,一部分是负类。法向量指向的一侧为正类,另一侧 为负类。
几何性质
首先在二维平面中我们计算点到直线的距离如下,这不难想象到三维空间及高维空间的点到平面的距离是如何计算的。


所以如上图即可以证明w是法向量 ,也可以推导出点到平面的距离公式。其中距离公式的分母是w的L2范数(欧式距离)。任意点到超平面的距离=将点代入平面方程的绝对值/法向量的模。
原始公式推导
西瓜书中给出

此时样本点到超平面的间隔为

注:分类不正确的情况下,求得的间隔为负数,不影响计算的最终结果。
定义了样本点到超平面的间隔后,我们继续定义样本训练集到超平面的间隔:训练集所有样本点到超平面的间隔的最小值

而支持向量机SVM算法的最终目的,就是获得最高的分类准确率,等同于找到训练集间隔最大的最优超平面。
下图是对于SVM原始公式推导(西瓜书和统计学习方法书中的推导个人认为略有不同,但是最终推导得出的结果是一样的)

其中需要注意的是对于超平面W*x+b=0 (这个时候w有个转置上标) 参数组(w,b)=(w*,b*)和 (w,b)=(kw*,kb*)表示的是同一个平面,即在等倍数缩放w,b结果表示的都是同一个平面。所以为了简化最优问题,令样本点到超平面的最小间隔为1.则
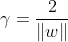
。这一改变对不等式约束及目标函数优化没有影响,也就是说它产生一个等价的最优化问题。

注意:将
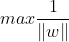
改为
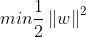
是为了后续的计算更简便,这两个是等价的。

最大间隔分离超平面的存在唯一性(李航老师的统计学习方法中第七章中讲的非常详细)
存在性易得,这里讨论一下唯一性:
假设问题存在两个最优解( W*1, b*1)和(W*2 ,b*2 )。根据假设因为要求最大化最小间隔,所以
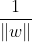
是相等的,也就意味着

其中c是一个常数。设

,由上述的公式可知,

因为公式的约束导致 c 此时是最小的
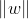
.所以最后不等式表明,式中的不等号可变为等号,即

,从而有
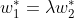
,
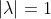
。若
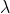
=-1,则w=0,(w,b)不是问题的可行解,矛盾。因此必有
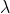
=1,即
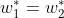
,所以两个最优解为
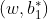
和
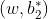
。

上图中的x1',x2'是集合{xi | yi = +1}中分别对应
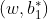
和
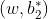
使得问题的不等式等号成立的点,同理x1''和x2''是集合{xi | yi = -1}分别对应
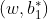
和
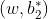
使问题的不等式等号成立的点。上述推导过程很清楚,最后一列公式是将x2'代入
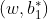
的超平面能够被分类正确所以满足

同理其他的式子也是将点分别代入超平面。最后两个不等式要取等号才能满足。推导过后得到 b是相同的,所以得到两个最优解是相同的,解的唯一性得证。
拉格朗日函数
在支持向量机和最大熵模型中都会用到拉格朗日的对偶性,主要为解决约束最优化问题,通过将原始问题转换为对偶问题求解。接下来就补充一下这方面的知识。
1.原始问题
先从求函数最小值开始:

求f(x)f(x)的最小值时x的取值,f(x)在
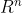
上连续可微(为什么要求连续可微?因为假设其连续可微根据高中知识,对函数求导,令导数为0即可求出最优解)。这时候我们对f(x)求导令导数为0就能取到极值了。若此时加入约束如下:

其中f(x),ci(x),hj(x)在
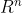
上连续可微我们称此约束最优化为原始问题,也是拉格朗日对偶性需要解决的问题。
此时我们直接求导是无法解决了,要是可以将约束条件转换为未知变量(把约束条件去掉)或许就可以找到答案了,而拉格朗日函数就是做这个的。
2.拉格朗日函数
这部分参考:及
为了求解原始问题,引进广义拉格朗日函数(generalized Lagrange function):

其中
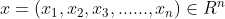
,
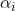
和
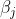
是拉格朗日乘子且

,式子看上去好像很复杂(哈哈哈真的复杂)其实是将原始问题的所有的约束条件加上新引入的变量(拉格朗日乘子)构成了一个新的函数,这样就是把约束条件转换为了未知变量。现在,把
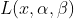
看作是关于
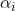
和
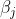
的函数,经过优化就是确定
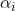
和
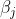
的值使得
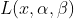
取得最大值(此过程中把x看做常量),确定了
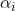
和
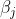
的值就可以得到
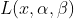
的最大值,,而此时

就是只和x有关的函数。
此时我们考虑x的函数:

下标P代表原始问题 ,其中,

有:

接下来分析证明x是否满足原始问题中的约束

。首先如果x违反了某个原始问题的约束,即存在某个i使得
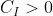
或者存在某个j使得
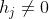
那么就会有

因为若某个i使得
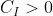
,则可令
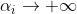
; 或者若某个j使得
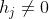
那么就可令
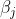
使
,而将其余各
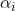
和
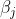
均取为0
所以如果考虑极小化问题,则:

这样可以发现它是与原始最优化问题等价的,即它们有相同的解。
对偶问题
上述公式为得到的原始问题的对偶问题。该对偶问题是极大极小问题,为了得到对偶问题的解,先求
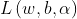
对w,b的极小,再求
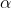
的极大。1.求
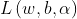
对w,b的极小。

所以得到

接着把上述式子回代入到拉格朗日函数中:

所以

推导式子中的m和最终N其实是一样的
2.求
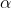
的极大,即是对偶问题:


























