1.SVM是什么
举个简单的例子,如下图所示
左图有三条直线
(1)虚线不能很好的进行分类
(2)两条实线能够实现分类(在该数据集中表现较好),但是这两个线性模型的判定便界很靠近样本点,在新的数据上可能不会表现得那么好。
右图一条实线
(1)该实线不仅分开了两种类别,还尽可能远离了最靠近的训练数据点,可以理解为SVM分类器在两种类别之间保持了一条尽可能宽敞的街道,因此SVM可以理解为最大间隔分类。
(2)该直线如果上升到多维,叫做分隔超平面,SVM分类器希望找到离分隔超平面最近的点,使其离分隔超平面尽可能的远,这些点到分隔面的距离被称为间隔,SVM思想是寻找最大间隔。
(3)支持向量就是离分隔超平面最近的那些点。
(4)支持向量机是一种分类器,之所以称为“机”是因为它会产生一个二值决策结果,即它是一种决策“机”。支持向量机的泛化错误率较低,即它具有良好的学习能力,且学习到的结果具有很好的推广性。这些优点使支持向量机十分流行,有人认为它是监督学习中最好的定式算法。

2.函数间隔Functional margin与几何间隔Geometrical margin
函数间隔定义如下

上式中y表示类别,wT*x+b=0则为超平面。
因此,在超平面(w,b)中关于T(训练集)中所有样本点(xi,yi)的函数间隔最小值(其中xi为特征,yi为结果标签,i表示第i个样本),即为该超平面关于训练集T的函数间隔

此函数间隔有个缺陷就是,在超平面w和b成比例改变时,如2w和2b,此时由上式知函数间隔也变成了两倍,而超平面不变,这里理解:超平面不变可以理解为2(wT*x+b)=0,2可以去掉,变成(wT*x+b)=0,因此超平面不变。我们希望的是在超平面不变(哪怕w和b随便成比例改变),函数间隔应该保持不变,这才是一个成熟的标尺。
因此我们引出了几何间隔的概念,所谓几何间隔实际上就是点到平面的物理距离。假定一个三维空间Ax+By+Cz+D=0(这里面|A,B,C|即为w向量),该超平面可能有多副面孔,比如6Ax+6By+6Cz+6D=0,不管其有多副面孔,某点到该平面的距离始终保持不变(所谓我自岿然不变,这才是一个成熟的标尺)。因此我们采用几何间隔作为距离判定标准。
在
公式推导,如下图

上述公式即为x0点沿着几何距离方向平移(r*w/||w||)距离,其中||w||为w的二阶范数(范数是一个类似于模的表示长度的概念),
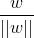
是单位向量(一个向量除以它的模称之为单位向量)。,由于x0是超平面上的点,因此必然满足f(x)=0,即WT*x+b=0,将此公式代入上式,进行计算,如下是推导过程:

因此可以知道,几何间隔=函数间隔除以||w||
3.最大间隔分类器Maximun Margin Classifier
如上图所示,我们需要使超平面离数据点的间隔越大,分类的确信度(confidence)就越大,上述实线为我们要找的超平面,又叫决策边界,虚线叫做间隔边界,超平面位于间隔边界中间,刚好使双方最大间隔值都为最大。
设定分类标签为1,和-1,则由上面推出的几何间隔=函数间隔/||w||,而函数间隔y*(W*x+b),要么为(-1)*(-1),要么为(1*1),都是等于1,因此这个时候几何间隔=1/|w|||,因此两个间隔边界距离为2/||w||。这里两直线的距离参考如下二维平面下的推导

因此最大间隔分类器的目标函数可以定义为:

st表示约束条件,该公式含义是,在相应的约束条件

下,求1/||w||的最大值,即求得最大的几何距离。如上图所示,对于支持向量上的点有,函数间隔

,而对于所有不是支持向量的点,则显然有

。
未完待续,对偶函数,针对非线性可分的数据,无法找到对应超平面的情况下,利用核函数等等......























