深度学习中sgd优化器的原理 sgd 优化器

优化器

目前优化器主要分为两个方向：

1. The accelerated SGD: SGD momemtum

2. The adaptive learning rate methods: Adam

 

 

SGDM：收敛慢，更好的精度，比较稳定，train和val的差距比较小

Adam：收敛快，可能不收敛，不那么稳定，generalization performance比较差。

 

 一、SGD家族

1. BGD、SGD

最初始的优化方法。向负梯度的方向更新。

TODO：更新为什么是从负梯度方向

 

BGD每一步迭代都使用训练集的所有内容，当数据集很大时，运行速度很慢。

SGD每次随机抽取一个样本，以此来更新参数，SGD计算的更快，但同时也波动更大。

折中取mini-batch GD每次计算n个样本，n取值一般在50~200。但它的问题是：收敛性不能保证

这几个方法都有以下通病：

1）学习率固定，无法动态调整。

　　如果学习率设大了，会一直在最小值附近波动，无法收敛；

　　如果学习率设小了，又会导致下降速度过慢。

　　我们更希望的是一开始学习率大，越到后面学习率越小。

2）所有方向上统一的缩放梯度，同时导致：不适用于稀疏数据。

　　数据稀疏时，我们更希望对出现频率低的特征进行大一点的更新。不然可能出现Z字型更新下降（因为一个方向比另一个方向更陡峭）

3）在高度非凸的误差函数优化过程中，无法避免陷入局部次优解或鞍点。

　　

 

4）参数更新方向只依赖于当前batch计算出的梯度，也可能导致十分不稳定的震荡。

　　数据量有限。

 

为保证SGD收敛，一般实际操作中，对学习率会进行线性衰减，例如除以迭代次数。但这种方法也需要提前设定好，无法自适应于数据集的特点。而且也还是无法解决问题2：稀疏数据问题.

 

 

2. 动量Momentum

SGD在数据稀疏的情况下容易被困住，即曲面的一个方向比另一个方向陡，这时SGD会Z字型走位震荡严重。

 

 Momentum梯度更新规则：

超参设定值：

r——一般取值0.9左右

借鉴了物理小球滚落的过程，当前梯度会带有上一时刻的动量，而这个动量同时也是各个时刻梯度的指数加权平均。相当于加入了惯性。引入了一阶动量。

前后梯度方向一致时，能加速学习；前后梯度方向不一致时，能抑制震荡。

1）增加了稳定性：不只是依赖于当前时刻的梯度，还考虑了以往时刻的梯度。在梯度方向有所改变的维度上更新速度变慢，可加快收敛并减小震荡；

2）收敛速度更快：惯性加持，在梯度方向不变的维度上速度更快；

3）还有一定摆脱局部最优的能力。

Momentum的缺点是什么呢？

 盲目沿着坡滚，如果能具备先知，快上坡就减速，适应性会更好

Nesterov accelerated gradient（NAG）

 

 

我们还希望可以根据参数的重要性而对不同的参数进行不同程度的更新

 

自适应优化

Adagrad

这个算法可以对低频的参数做较大的更新，对高频的做较小的更新。对稀疏数据表现很好。

 梯度更新规则：

 

 

 

 

 

 g_t,i是 t 时刻参数 θ 的梯度；G_t 是对角矩阵，(i, i)元素是 t 时刻参数 θ 的梯度 g_t,i 的平方和 

优点是减少了学习率的手动调节；

缺点是分母会不断积累，这样学习率急剧下降，最终会收缩变得非常小。

 

Adadelta

对Adagrad的改进

 

 

 把Adagrad中分母的 G 换成了 E[g²]，下半部分整个更号也可以写作 RMS[g]_t

其中 E[g²] 的 t 时刻依赖于前一时刻的平均和当前的梯度，计算公式如下：

 

此外，还将学习率 a 换成 RMS[Δθ]_t-1

 

 超参数设定值：

r 一般为0.9

 

RMSProp

对Adagrad的改进。引入衰减系数，让  r  每回和都衰减一定比例。

相比于Adagrad，更好的解决了深度学习中过早结束的问题。和Adadelt的第一种形式相同。

适合处理非平稳目标，对于RNN效果很好

 

 

 

 Hinton建议 r 设为0.9，学习率 a 设为 0.001

但又引入了新的超参，衰减系数p，依然依赖于全局学习速率

 

Adam

另一种计算每个参数的自适应学习率的方法。在DL中是目前最常见的优化器。

本质上是带有动量项的RMSprop，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率

除了像RMSprop一样存储了过去梯度的平方 vt 的指数衰减平均值，也像momentum一样保持了过去梯度mt的指数衰减平均值

 

 

mtmt和 vtvt 被初始化为 0 向量，那它们就会向 0 偏置，所以做了偏差校正， 

通过计算偏差校正后的 mt 和 vt 来抵消这些偏差： 

梯度更新规则：

 

 

 

 

 超参数设定值：

建议 β1 ＝ 0.9，β2 ＝ 0.999，ϵ ＝ 10e−8

优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

实践证明，Adam比其它自适应学习方法效果更好。

 

 

 

 

 

 

对比

 

 

 

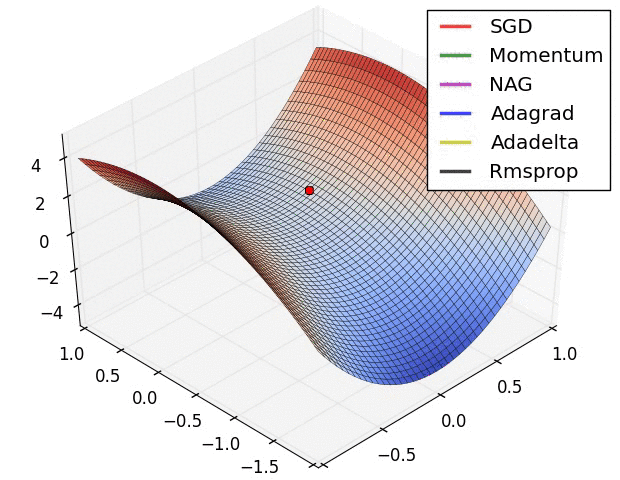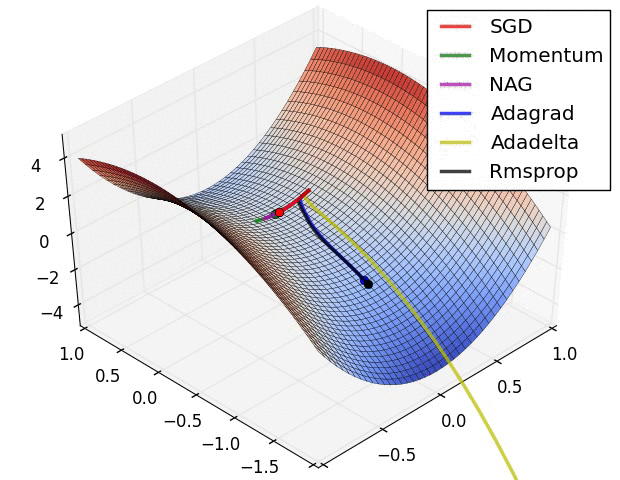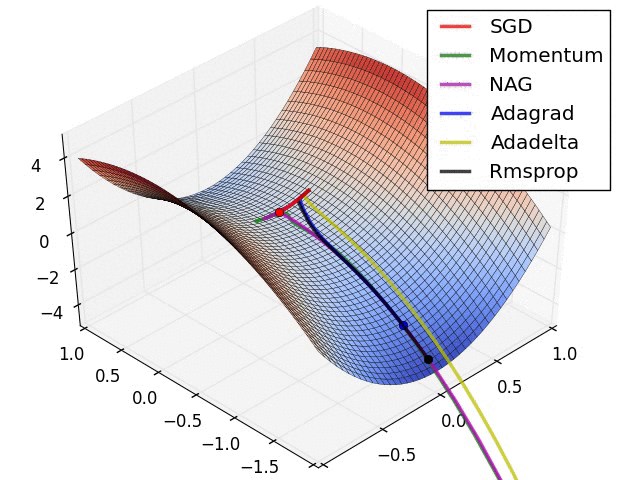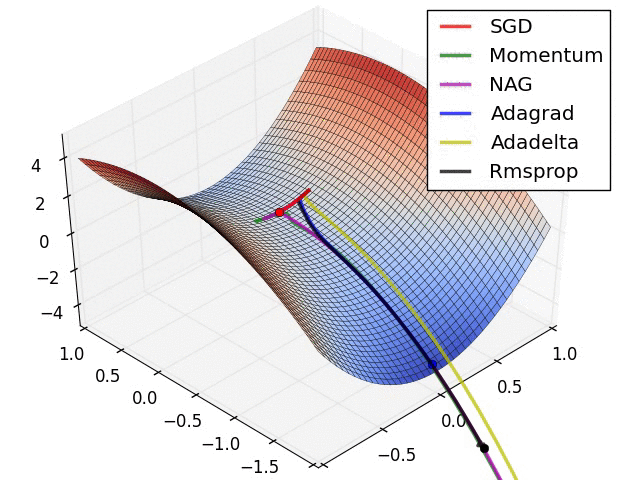
Adagrad相比sgd和momentum更稳定，即不需要怎么调参。

而精调的sgd和momentum无论是收敛速度还是precision都比adagrad要好一些，其中momentum又优于sgd

 

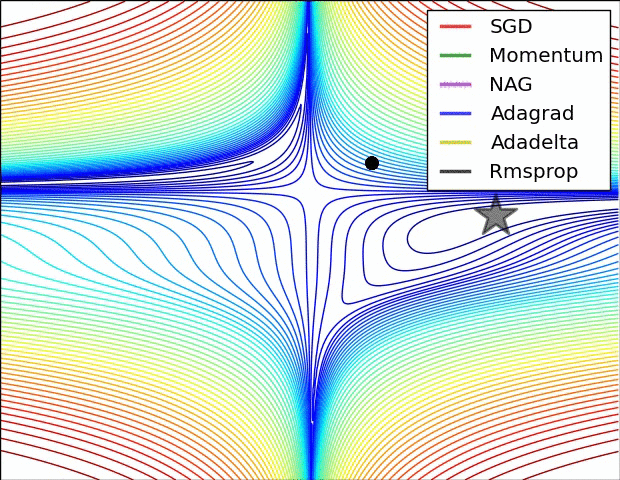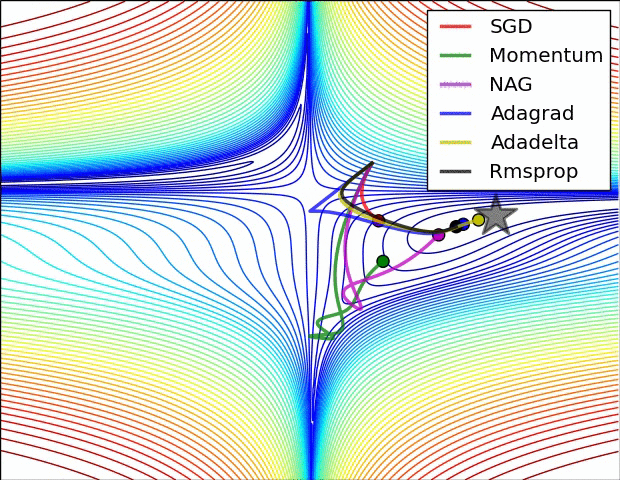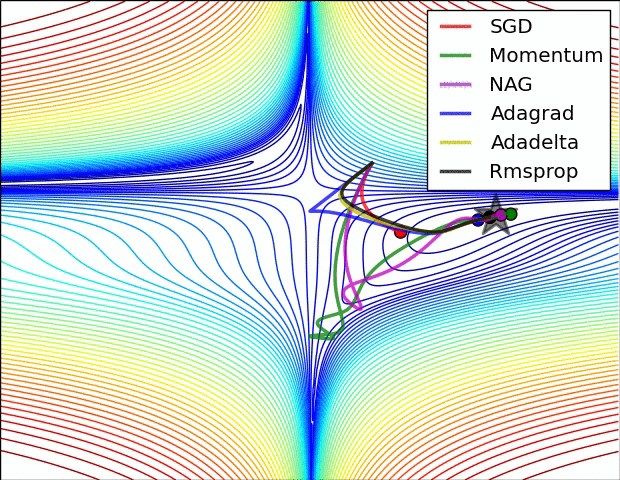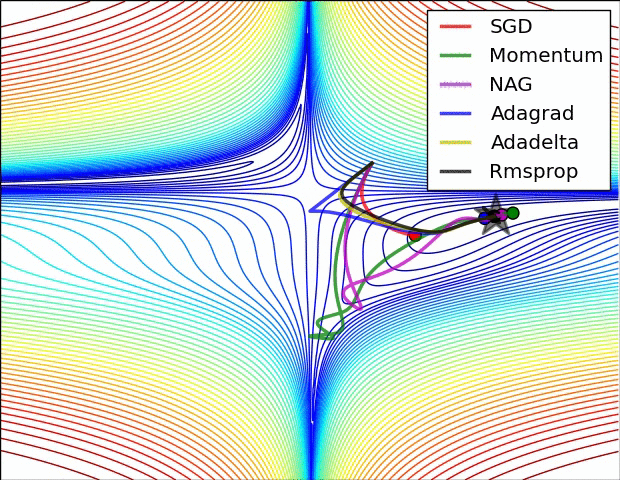
Adagrad, Adadelta, RMSprop 几乎很快就找到了正确的方向并前进，收敛速度也相当快，而其它方法要么很慢，要么走了很多弯路才找到。

 

如何选择

如果数据是稀疏的，就使用自适应方法，即 Adagrad, Adadelta, RMSprop, Adam

其中RMSProp、Adadelta、Adam在很多情况下的效果是相似的。

Adam就是在RMSprop的基础上加了bias-correction和momentum

随着梯度变的稀疏，Adam比RMSprop效果会好。

整体来讲，Adam是最好的选择。

如果需要更快的收敛、或是训练更深更复杂的神经网络，需要一种自适应的算法。